5.4/5.5 Sum and Difference Formulas and Reduction Formulas and Lots OF FORMULAS

VERY IMPORTANT

Proof for sum and difference formulas

Videos

What you can do with these formulas

You can use identities to rewrite

trigonometric expressions and you can rewrite a trigonometric

expression in a form that helps you solve the problem

SUM AND DIFFERENCE FORMULAS

• Note: To derive others, manipulate algebraically using these numbered formulas.

Sin (M+N)

sin(m + n) = sin m cos n + cos m sin n 

SIN (M-N)

sin(m − n) = sin m cos n − cos m sin n

cos is an even function so sin(m)cos(-n) + cosm sin(-n) get sin m cos n -cos m sin n

COS (M + N)

cos m cos n − sin m sin n

COS (M − N)

cos m cos n + sin m sin n

cos is an even function and sin is an odd function so cosmcos(-n) - sinmsin(-n) is cos m cos n + sin m sin n

TAN(M+N)

(tan m + tan n)/(1 − tan m tan n)

TAN(M-N)

(tan m − tan n)/(1 + tan m tan n)

Notes Example problems and what you can prove

Prove using the Sum and difference formulas 

1. Sin(pie/2-x)=cosx

2. Cos(pie/2-x)=sinx

3. Sin(pie-x)

4. Sin(pie+x)

5. cos(pie-x)

6. cos(pie+x)

7. tan(pie-x)

8. tan(pie+x)

Solve 

cos75 

sin(pie/12)

sin15 

Sin42cos12- cos42sin12 

Cos(theta-3pie/2)

Tan(theta+3pie)

Good one solve

cos(arctan1+arccosx) use triangle to solve 

MAIN EXAMPLE OF USING SUM AND DIFFERENCE. SOLVING AND EQUATION

Find all solutions of sin(x+pie/4)+sin(x-pie/4) = -1 in the interval [0,2pie)

use the sin sum formulas to get 

sinxcospie/4+cosxsinpie/4 + sinxcospie/4 - cosxsinpie/4 =-1

and can cross out the 2nd and 4th terms and get

2sinxcospie/4=-1.  and know from unit circle value that cospie/4 is root2/2. 

so 2(sinx)(root2/2)=-1 

and divide both sides by 2 to get (sinx)(root2/2)=-1/2 and then  multiply by root2/2 to get 

sinx=-root2/2.

and know by using unit circle x=5pie/4 and x=7pie/4. and then check

Sum and difference HW

Page 423

Part 1 do Exs. 1-21 (odds), 31-36,

Sum and difference HW

Page 424

Part 2 do 37-63 (odds), 69-72. 

5.5 ALL THE OTHER TRIG FORMULAS

Overview of section

In this section you will study the 4 other categories of Trig identities

1. Products of Trig functions such as sinmcosn

2. functions of multiple angles such as sin km and cos kn

3. squares of trigonometric functions such as sin²x

4. involves functions of half-angles such as sin(x/2)

1. PRODUCT- TO- SUM

• Formulas (labeled a-d) for future derivation

• Derivations (Add/Subtract sum equations for all 4):

easily verified using the sum and difference formulas discussed in the preceding section.

Product-to-sum formulas are used in calculus to evaluate integrals involving the products of sines and cosines of two different angles.

PRODUCT- TO- SUM example problems

Rewrite the product cos 5x sin 4x as a sum or difference.

(A) sin M cos N

and derivation

• 1/2 [sin(M + N) + sin(M − N)]

• For formula A you do sum equation 1 + sum equation 2 = 

  • Add sin(M + N) + sin(M − N) = 2 sin M cos N

(B) cos M sin N

and derivation

1/2 [sin(M + N) − sin(M − N)]

• For Formula B you do sum equation 1- sum equation 2 =

  • Sin(m+n)-sin(m-n)= 2 cosM sinN

(C) cos M cos N

and derivation

1/2 [cos(M + N) + cos(M − N)]

• For Formula C you do sum equation 3 + sum equation 4 =

  • Cos(m+n)+cos(m-n)= 2cosM cosN

D) sin M sin N

and derivation

1/2 [cos(M − N) − cos(M + N)]

• For formula D you do sum equation 4 - sum equation 3 

  • Cos(m-n)-cos(m+n) = 2sinM sinN

1. SUM-TO-PRODUCT RULES (WITH x & y)

   Derivation for all have to  Derivations (let  x = M + N and y = M − N): so  m=(x+y)/2 and n=(x-y)/2

Occasionally, it is useful to reverse the procedure and write a sum of trigonometric functions as a product. This can be accomplished with the following sum-to-product formulas.

sin x + sin y

and derivation

2 sin(x+y/ 2)cos(x-y/ 2)

SO now you just plug those values into the Product to sum formulas

so if I plug into  formula A in you get Sin(x+y)/2 cos (x-y)/2 = 1/2(sin(x)+sin(y) which simplifies to get your formula

sin x - sin y

and derivation

2 cos(x+y/ 2)sin(x-y/ 2)

Derivations (let  x = M + N and y = M − N): so  m=(x+y)/2 and n=(x-y)/2

SO now you just plug those values into the Product to sum formulas

So if I plug into  formula B you get cos(x+y/2)sin(x-y/2)=1/2(sinx-siny) which simplifies to get your formula

cos x + cos y

and derivation

2cos(x+y/ 2)cos(x-y/ 2)

  Derivations (let  x = M + N and y = M − N): so  m=(x+y)/2 and n=(x-y)/2

SO now you just plug those values into the Product to sum formulas

So If I plug into formula C you get cos(x+y/2)cos(x-y/2)=1/2(cosx+cosy)

cos y - cos x

and derivation

      

2sin(x+y/ 2)sin(x-y/ 2)

Derivations (let  x = M + N and y = M − N): so  m=(x+y)/2 and n=(x-y)/2

SO now you just plug those values into the Product to sum formulas

So If I plug into formula D you get sin(x+y/2)sin(x-y/2)=1/2(cosy-cosx)

SUM-TO-PRODUCT RULES example problem

cos 195 degreees + cos 105 degrees

SUM-TO-PRODUCT RULES example problem Verifying TRIG WITH IT

IMPORTANT EXAMPLE

verify the identity

(sint+sin3t)/(cost+cos3t) = tan 2t

Use Sum-to-product formulas to get (2sin((t+3t)/2) cos((t-3t)/2))/(2cos((t+3t)/2)cos((t-3t)/2))

and simplifies to  2sin(2t)cos(-t)/2cos(2t)cos(-t). and you can cross out the 2 and the cos(-t) to get

sin(2t)/cos(2t) which is tan(2t)

SUM-TO-PRODUCT RULES example problem SOLVING EQUATION WITH IT

IMPORTANT EXAMPLE

solve sin 5x +sin 3x = 0

use sum to product rule to get 2sin((5x+3x)/2)cos((5x-3x)/2)=0

equals 2sin4xcosx=0

and then divide by 2 to get sin4xcosx=0

so sin4x=0 and cosx=0

x=npie/4 . and x=pie/2+ npie

2. Multiple angle/ Double angle identities

all derivations by using sum and difference formulas and like this trigfunction(x+x)=and then do it.

You should learn the double-angle formulas because they are used often in trigonometry and calculus. For proofs of the formulas, see Proofs in Mathematics on page 425.

sin(2x)

and derivation

 2 sin x cos x

• to derive these formulas you just do the sum formula for each

  • For Sin 2x= Sin(x+x) and then you do the sum formula for sin and get 2(sinxcosx)

cos(2x)

and derivation

• THIS FORMULA SUPER IMPORTANT BECAUSE IT IS BASE OF POWER REDUCTION IDENTITIES. The power reduction identities are derived by rearranging specific forms of the double-angle formula to solve for the squared term

cos² x − sin² x 

• Which could also be 2cos^2 x -1 because -sin^2 x is also -1+cos^2 x 

• Could also be 1-2sin^2 x because cos^2 x is also 1-sin^2 x 

• To derive these formulas you just do the sum formula for each

  • For Cos 2x= Cos(x+x) and then you do the sum formula for cos and get cos^2 x - sin^2 x 

Tan(2x)

and derivation

2 tan x / (1 − tan² x)

To derive these formulas you just do the sum formula for each

• For Tan 2x= Tan(x+x) and then you do the sum formula for Tan and get (2tanx)/(1-tan^2 x)

1. Multiple angle/ Double angle identities Example solving an equation 
   SUPER IMPORTANT EXAMPLE

solve 

2cosx + sin2x = 0 

Use the sin double angle formula

2cosx+2 sin x cos x = 0

factor 

2cosx(1+sinx)=0

2cosx=0 1+sinx=0

cosx=0. sinx=-1

x= pie/2, 3pie/2 and x= 3pie/2

General solution

x=pie/2 +2pien. x=3pie/2 + 2pie n

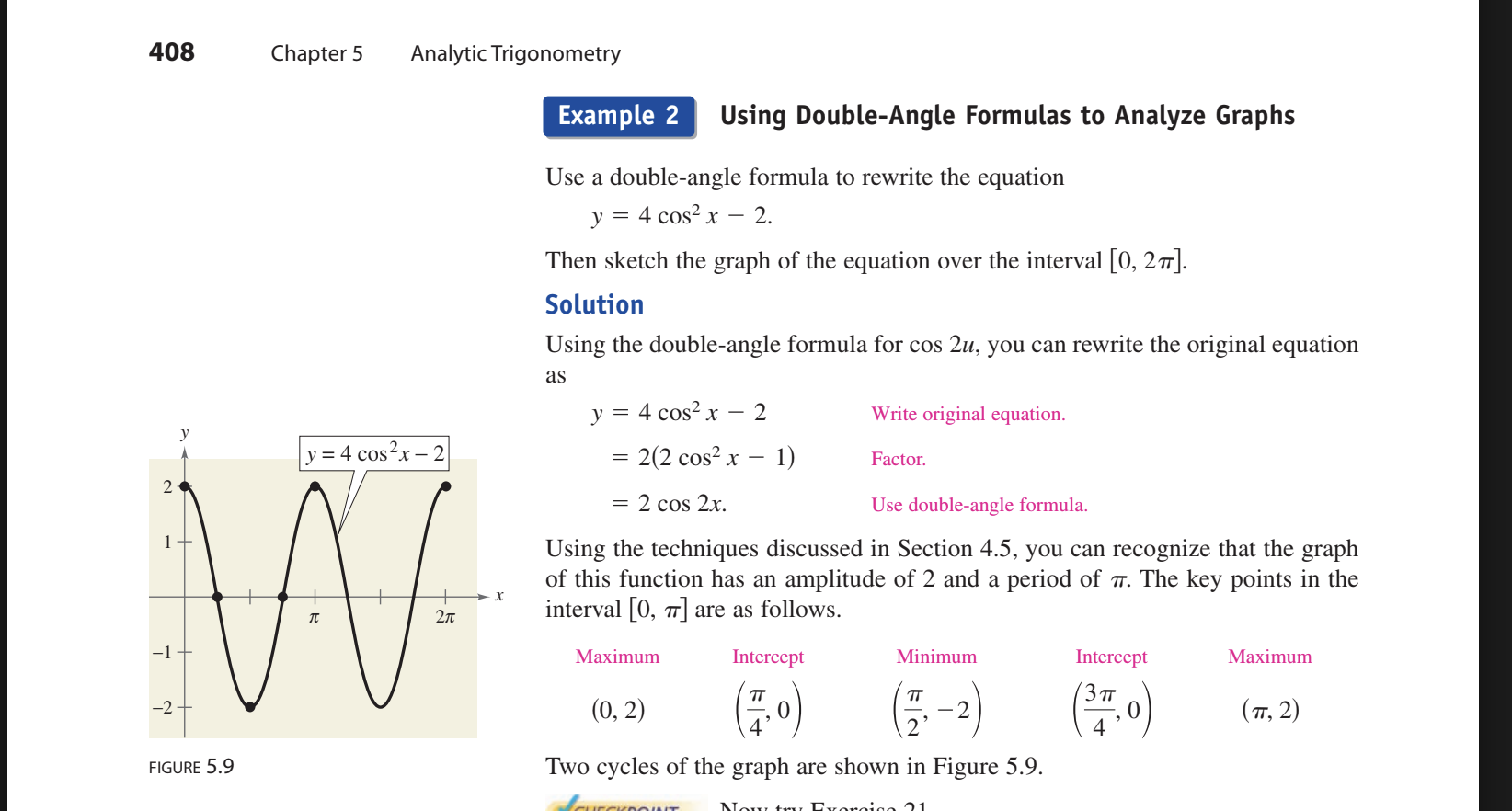
2. Multiple angle/ Double angle identities Example USING to analyze graphs
   SUPER IMPORTANT EXAMPLE

Use a double-angle formula to rewrite the equation

y=4cos²x-2

Then sketch the graph of the equation over the interval [0,2pie)

y=4cos²x-2

y=2(cos²x-1)

then using the double angle formulas you get

y=2(cos2x)

Then you can graph this 

Amplititude 2 and period pie and then just graph it.

3. Multiple angle/ Double angle identities Example Evaluating Functions Involving Double Angles
   

Use the following to find sin(2theta), cos(2theta), and tan(2theta)

cos(theta)= 5/13,  3pie/2<theta<2pie

so know that it is in the 4th quadrant and sin would be -12/13

and then you can use those values to get them

Sin(2theta)= 2sinxcosx= 2(-12/13)( 5/13) = -120/169

Cos(2theta)=cos²x-sin²x= (5/13)²-(-12/13)²= (-119/169)

Tan(2theta)= sin2x/cos2x= -120/169/-119/169= 120/119

3. Power Reduction Identitites

Derivation using the cos double angle formulas

These allow you to go from a squared trig to a non squared term and the other way around 

These formulas are derived by the double angle formula for COS. The Two forms of cos(2x) allow solving for sin² θ or cos² θ; choose the form depending on which variable you need to isolate.

The double-angle formulas can be used to obtain the following power-reducing formulas. Example 5 shows a typical power reduction that is used in calculus.

sin² x

and derivation 

(1 − cos(2x)) / 2

• To get the sin formula you use the Cos 2x double angle formula cos2x=1-2sin^2 x that has the sin^2 x  and then you just solve for sin^2 x and get Sin^2 x = (1-cos2x)/2

cos² x 

and derivation

(1 + cos(2x)) / 2

• To get the cos formula you use the Cos 2x double angle formula Cos2x=2cos^2 x -1 because it has the cos^2 x and then you just solve for Cos^ 2 x and get cos^2 x = (1+cos2x)/2

tan² x 

and derivation

(1 − cos(2x))/ (1 + cos(2x))

• To get the tan formula you use the 2 sin^2 x and cos ^2 x formulas and the identity that tan^2 x = Sin^2 x / Cos^2 x  so then you plug in the formulas  to get ( (1-cos2x)/2 )/ ((1+cos 2x)/2)  and then get the Tan formula 

Power Reduction Identitites example

IMPORTANT

rewrite sin^4 x as a sum of first powers of the cosines of multiple angles.

sin^4 x = (sin²x)²

use power reduction formula to get ((1-cos2x)/2)²  

can expand this and get 1/4(1-2cos2x+cos²2x)

use power reduction formula again and get 1/4(1-2cos2x+((1+cos4x)/2)

and then distribute to get 1/4-1/2cos2x+1/8+1/8 cos 4x

and then factor out the common factor

and get 1/8(3 - 4cos2x+cos4x)

4. Half angle formulas

The signs of sin(u/2) and cos(u/2) depend on the quadrant in which u/2 lies.

DERIVED BY USING POWER REDUCTION FORMULAS

You can derive some useful alternative forms of the power-reducing formulas by replacing with The results are called half-angle formulas.

sin(x/2)

and derivation

±√((1-cosx)/2)

• For sin(x/2) you use the reduction formula for sin  which is sin^2 x = (1 − cos(2x)) / 2 and then just plug x as x/2 and then get sin ^2 (x/2) = (1-cos(x))/2) and then you solve for sin (x/2) by square rooting both sides 

cos(x/2)

and derivation

±√((1 + cos x)/2) 

• For cos(x/2) you use the reduction formula for cos which is cos² x = (1 + cos(2x)) / 2 and then plug in x as (x/2) so get cox ^2 (x/2) = (1+cos(x))/2) and then you solve for cos(x/2) by square rooting both sides 

tan(x/2)

And derivation

sinx/(1+cosx) or (1-cosx)/(sinx)

• For tan(x/2) you use the sin/cos identitiy and do the sin half angle formula over the cos half angle formula and then get it.

Half angle formulas example problem

Good example

find the exact value of sin 165

165 s half of 33 and so

sin(330/2)=plus minus (root (1-cosx)/2) Sin positive in quadrant 2 so positive

Sin 165=+(root (1-cos330)/2)= root(1-root3/2)/2) and that give (root (2-root3)/4) and then can pull the 4 out of the root and get ½ (root(2-root3))

Half angle formulas example problem solving TRIG EQUATION

SUPER IMPORTANT

find all the solutions of 2-sin²x = 2cos² x/2 in the interval [0,2pie)

Use half angle formula to get 2-sin²x=2(plus minus root(1+cosx)/2)

can simplify by using the square root get 2-sin²x=2(1+cosx)/2

and that simplifies to

2-sin²x=1+cosx

and then you can use the pythagorean identity to get

2-(1-cos²x)=1+cosx

and 1+cos²x=1+cosx. and isolte on one side to get 

cos²x-cosx=0 factor to get

cos(cosx-1)=0. 

and x=pie/2, 3pie/2 and x=0

HW part 1 9-33 odds

HW part 2 41-81 odds 87, 89

HW part 3 95-109 odds