Calculus Final Exam

when is a function said to be injective?

if whenever f(a)=f(b), then a=b.

do vert line tests or horiz line tests determine if you have a function?

vertical line tests

do vert line tests or horiz line tests determine if you have a one-to-one function?

horizontal line tests

even function

f(-x)=f(x)

odd function

f(-x)=-f(x)

true or false: a function has an inverse iff it is injective

true

log_b(AC)

log_bA+ log_bC

log_bb= ?

1

log_b(A/C)

log_bA-log_bC

log_bA^R

Rlog_bA

log 1 = ?

0

if log_aB = n, aⁿ=?

b

if f(x) = b^x, f^-1(x) = ?

log_bx

if f(log_bx)=x, what does b^log_bx=?

x

trig identity

cos²+sin²=1

sin (pi/6)

1/2

cos (pi/6)

(sqrt3)/2

sin (2x) = ?

2 sinx cosx

sin (A+B)

sinAcosB + sinBcosA

sin²x= ?

1/2(1-cos 2x)

cos²x = ?

1/2(1+ cos 2x)

log_bx

(log_ax)/(log_ab)

how to find horizontal asymptotes

if the degree of the denominator is greater - > the asymptote is y=0. 

if the degrees are equal - > ratio of the the leading coefficients

if the degree of the numerator is greater - > no horizontal asymptote

the tan line to the curve y = f(x) at point f(x, f(x)) has the slope m = 

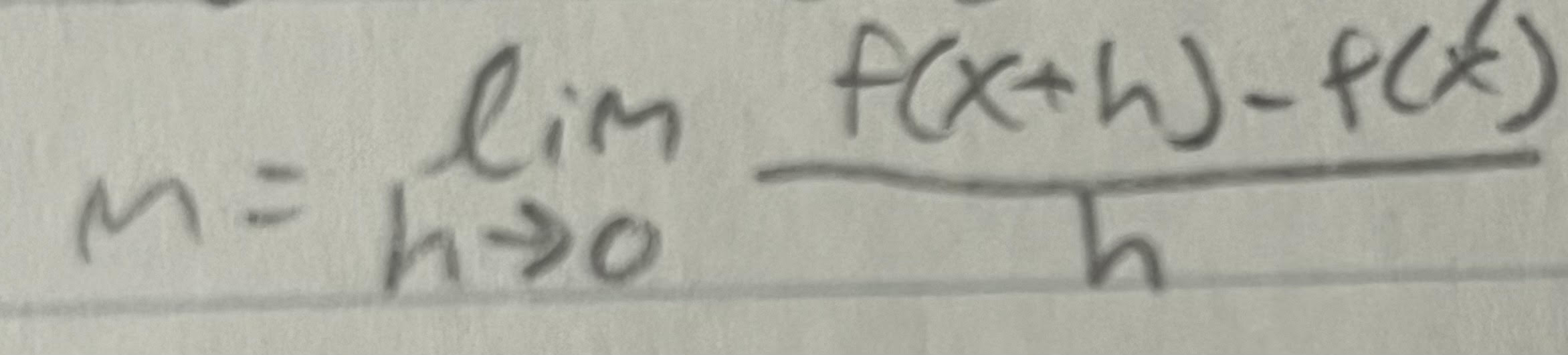
a³-b³

(a-b)(a²+ab+b²)

a³+b³

(a+b)(a²-ab+b²)

Squeeze Theorem

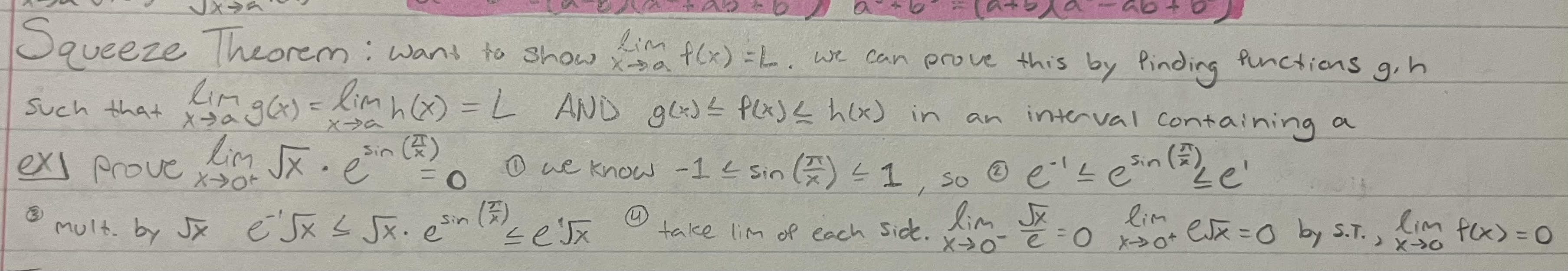
Intermediate Value Theorem

f(x) is cont. on a closed interval [a,b] then for any N between f(a) and f(b) we can find c in the interval (a,b) s.t. f( c ) = N

d/dx C = ?

0

d/dx e^{x = ?}

e^x

theorem about composition of functions

if g is cont. at a and f is cont. at g(a) then their composition f(g (x)) is cont. at a.

d/dx xⁿ = ?

nx^n-1

(f+ g)’ = ?

f’ + g’

(cf(x))’ = ?

c f’(x)

d/dx f(g(x)) =

f’(g(x)) g’(x)

(f(x)g(x))’ =

f’(x)g(x) + f(x)g’(x)

(f(x)/g(x))’ =

(f’(x)g(x) - f(x)g’(x))/g²(x)

cos’(x) 

-sin (x)

sin’(x)

cos (x)

tan’(x) 

sec²(x)

sec’ (x)

sec (x) tan (x)

csc’(x)

-csc (x) tan (x)

cot’(x)

-csc²(x)

d/dx (a^u)

a^uln (a) du/dx

equation for linearization

y = f(a) + f’(a)(x-a)

y = mx to b form : y = f’(a)x + b

where b = f(a) - f’(a)a

sinh x

(e^x-e^-x)/2

cosh x

(e^x+ e^-x)/2

tanh x

(e^x-e^-x)/(e^x+ e^-x)

sinh (-x) =

-sinh (x) 

so sinh (x) is odd

cosh (-x)

cosh (x)

so cosh (x) is even 

hyperbolic trig identity (DIFFERENT than the reg one)

cosh x²-sinh x²=1

critical number

any x-value in the domain where f’(x) is either 0 or UND

where must abs. max and min of cont. function [a,b] occur?

@ crit pts or endpts

Rolle’s Theorem

Let f(x) be cont on [a,b] and differentiable on (a,b). If f(a) = f(b), then there exists c in (a,b) s.t. f’( c ) = 0

Mean value theorem

let f(x) be cont on [a,b] and differentiable on (a,b). Then there exists a c in (a,b) s.t. (f(b)-f(a))/(b-a) = f’( c ) 

there may be more than 1 value of c

if f’(a) < 0 is f decreasing or increasing near a?

decreasing

if f”(a) > 0 is f concave up or concave down?

concave up

2nd derivative test

let c be in the domain of f(x) where f’( c ) = 0 and suppose f’’(x) is cont. near c. if f’’ ( c ) > 0 then f has a local min at c. if f’’( c )< 0 then f has a local max at c.

L’hopital’s rule

if a limit has the indeterminant form 0/0 or inf/inf, you can take the derivatives of the numerator and denominator seperately to find the limito

optimization

take derivative of eqn and find max/min

slant asymptote definition

y=mx + b is said to be a slant/oblique asymptote to f(x) if lim x→+- inf f(x) - (mx + b) = 0

antiderivative of xⁿ

1/(n+1) xⁿ⁺¹+C

antiderivative of x^-1

ln |x| + C

how to find horizontal asymptotes

if the numerator’s degree is less than the denominator’s, the HA is y=0. if they are equal, it’s the ratio of their leading coefficients. if the numerator’s degree is greater, there is no HA. for other functions, take the lim as x→+- infiniti