Long Term Finance: Bonds, Equities & Sustainable Financ

Chapter 6 + 7

What Is a Bond?

A bond is a long-term debt security issued by governments or corporations to borrow money.

You loan money to the issuer → they pay you interest periodically → repay the principal at maturity.

E.g. Company borrows £1,000 for 30 years, pays interest yearly, and returns £1,000 at the end.

Coupon

The stated interest payment paid on a bond.

Annual coupon = coupon rate x face value

E.g. 12% coupon on £1,000 face value: 0.12 × 1000 = £120 per year

Face Value (Par Value)

The principal amount repaid at maturity or end of term (usually £1,000).

E.g. Investor receives £1,000 at maturity, regardless of earlier bond price.

Coupon Rate

Annual coupon ÷ face value of a bond

Coupon rate = Coupon payment/ face value

E.g. £120 / £1,000 = 12%

Maturity / Time to Maturity

The date when face value is repaid.

E.g. A 30-year bond issued today matures in 30 years.

Redeemable vs. Irredeemable Bonds

Redeemable Bond: Has a maturity date.
Irredeemable Bond (Consol): Has no maturity date → behaves like a perpetuity.

E.g. UK consols pay interest forever and never return principal.

Yield to Maturity (YTM)

The market-required rate of return on a bond.

The interest rate that makes the present value of all cash flows equal the current bond price.

YTM determines how much the bond should be worth.

Basic Bond Valuation Formula

A bond = PV annuity (coupons) + PV lump sum (face value).

Bond value = C x (1 - (1 + r)^-t / r) + F / (1+r)^t

• C = coupon

• F = face value

• t = number of periods

• r = YTM per period

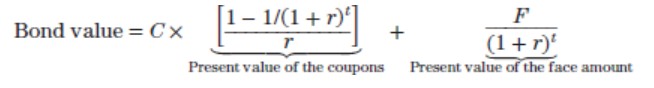
Conegliano bond example

• C = £80

• F = £1000

• t = 10

• r = 8%

Compute PV of coupons: PV annuity = 80 x (1- (1.08)^-10 / 0.08) = 536.81

Compute PV of face value: PV face = 1000/ 1.08^10 = 463.19

Total bond value: 536.81 + 463.19 = £1000 → sells at par (exactly face value) With an £80 coupon, this bond pays exactly 8 per cent interest only when it sells for £1,000 as the going interest in the market is 8%.

Coupon rate = YTM

Discount Bond

Bond sells below face value.

Occurs when Coupon rate is less than YTM

E.g. Bond with 8% coupon when market rate is 10%.
Price ≈ £885.

Premium Bond

Bond sells above face value.

Occurs when coupon rate is greater than YTM

E.g. 8% coupon when market rate is 6% → Price ≈ £1,136.

Why Bond Prices Change

Bond price and interest rate relationship:

Interest Rates ↑ → Bond Prices ↓Interest Rates ↓ → Bond Prices ↑

Reason: Cash flows are fixed, but discount rate changes.

Interest Rate Risk

Risk that bond prices will fluctuate when interest rates change.

Two factors increase risk:

1. Longer maturity → Higher risk

Changes in rates affect long-term discounting more drastically.

2. Lower coupon → Higher risk

More of the bond’s value is from distant face value → more sensitive to rate changes.

Maturity Example

Compare price sensitivity:

• 1-year bond → small price change

• 30-year bond → large price change

Longer bonds’ values depend heavily on distant discounting.

Coupon Example

Compare:

• 3% coupon bond

• 10% coupon bond

Both have same maturity → the low-coupon bond reacts more sharply to rate changes.

Finding YTM (Trial & Error)

You know:

• Price

• Coupon

• Face value

• Maturity

You solve for the unknown r in: Price (bond value) = C( 1 - (1 + r)^-t / r) + F/ (1 + r)^t

You cannot isolate r algebraically.

Method:
Try different r until both sides match (like solving annuity interest rates).

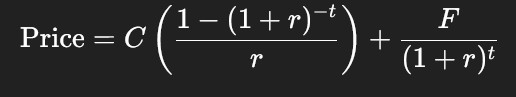
Trial-and-Error Example

Bond:

• 6 years

• Coupon = £80

• Face value = £1000

• Price = £955.14

Check YTM:

Try 8% → Too low (price too high).
Try 10% → Too high (price too low).
Try 9% → Matches the given price.

✔ YTM = 9%

Current Yield

Measures only the income return.

bond’s annual coupon divided by its price.

Current yield = Annual coupon / price

E.g. £80 / £955.14 = 0.0838 = 8.38%

Why different from YTM?

• Current Yield ignores capital gain/loss.

• YTM includes both coupon + price return.

Price Gain/Loss Effect

• Discount bond → built-in gain at maturity

• Premium bond → built-in loss at maturity

Current yield misses this → YTM adjusts for it.

What Affects Bond Prices

1. Coupon size

2. Market interest rates

3. Time to maturity

4. Discount/premium structure

5. Required yield by investors

Bond price = present value of fixed cash flows

What Are Bond Ratings?

Bond ratings are professional assessments of a bond issuer’s creditworthiness—how likely they are to repay their debt.

A rating tells investors how risky a bond is in terms of default risk, not price volatility.

E.g. Moody's, S&P, and Fitch grade bonds from AAA (very safe) to D (default).

Who Gives Bond Ratings?

The three main rating agencies:

1. Moody’s

2. Standard & Poor’s (S&P)

3. Fitch

These agencies are paid by firms/governments to rate their debt.

What Do Bond Ratings Measure?

ond ratings measure only default risk.

Important:
They do not measure:

• interest rate risk

• price volatility

A highly rated AAA bond can still fluctuate in price if market interest rates change.

Investment Grade vs. Junk Grade

Investment-Grade Bonds (safer):

• S&P / Fitch: BBB or above

• Moody’s: Baa or above

Junk Bonds (high risk, high yield):

• Rated below BBB / Baa

• Also called high-yield bonds

Example:
A BB bond = junk bond → higher chance of default → higher interest rate.

Rating Scales (Quick Guide)

S&P / Fitch:

• AAA

• AA

• A

• BBB → investment grade ends here

• BB, B, CCC, CC, C, D → junk

Moody’s:

• Aaa

• Aa

• A

• Baa → investment grade ends

• Ba, B, Caa, Ca, C → junk

Fallen Angels

Investment-grade bonds that are downgraded into junk territory.

E.g. During COVID-19, many firms lost revenue → downgraded by S&P.

Determinants of Credit Ratings

Credit rating agencies look at:

1. Sovereign (government) risk factors

2. Corporate risk factors

3. Macroeconomic conditions

4. Industry performance

5. Bond-specific features

Some are measurable, others are subjective.

Sovereign Bond Rating Factors

1. Political Risk: Government stability, Corruption levels, Transparency, Security

2. Economic Strength: GDP growth, Income inequality, Efficiency of public sector, Financial sector quality, Workforce flexibility

3. Government Debt Levels: High debt → lower rating

4. Monetary & Fiscal Flexibility: Independent central bank, Good quality economic data, Sensible budget spending, Ability to respond to shocks

Corporate Bond Rating Factors

1. Financial Risk (Most Important): Ability to make debt payments, Liquidity, Cash flow strength

2. Company Debt Burden: Increasing or decreasing debt? Is leverage manageable?

3. Capex Plans: Large upcoming spending → increases risk

4. Forecast Earnings: Will profits be enough to pay debt?

If a company looks less able to repay debt → lower rating.

Macroeconomic Factors That Affect Ratings

Examples that change credit ratings:

• Rising inflation → borrowing becomes more expensive

• Global oil price increases → higher production costs → lower profits

• Currency movements → affect companies with foreign debt

• Economic recessions → lower revenue → rating downgrades

Example:
Oil price spikes can cause manufacturing firms to miss earnings forecasts → rating drops.

Industry-Specific Factors

• Declining industries → lower ratings

• High-growth or stable industries → better ratings

• Regulatory changes also matter

Example:
Tightened environmental rules can hurt oil companies more than tech firms.

Bond-Specific Factors

Some bond structures are riskier:

• Subordinated (junior) debt → lower rating

• Secured debt → higher rating (assets back it)

• Callable bonds → often riskier to investors

Why Ratings Matter

Higher credit rating →

• lower default risk

• lower interest rate required

• cheaper borrowing for the issuer

Lower credit rating →

• higher interest rate demanded → higher bond coupon

• more expensive borrowing

• harder to issue new debt

Ratings Can Change

Ratings are not fixed. They change when:

• Company profits fall

• Debt rises too much

• Economic conditions worsen

• Political instability grows (for governments)

Example:
Many firms were downgraded in 2020 during COVID-19.

Why Investors Care

Ratings help investors judge:

• how risky a bond is

• whether the return is worth the risk

• whether it fits their investment rules (many funds must hold investment-grade bonds)

Why Companies Pay for Ratings

Because ratings influence:

• borrowing costs

• investor interest

• ability to issue bonds

• company reputation

Higher rating → cheaper funding → competitive advantage.

Why Shares Are Harder to Value Than Bonds

Shares are harder to value because:

1. Dividends (cash flows) are uncertain

2. Shares have no maturity → infinite life

3. Required return (R) is not directly observable

Despite this, we can estimate share value using present value of expected future dividends.

Basic Equity Valuation Idea

The value of a share today (P₀) = present value of all future dividends.

Values of share price today = the discounted value of all future dividends. 

no matter what the share price is, the present value is essentially zero if we push the sale of the equity far enough away.1 We are eventually left with the result that the current price of the equity is the present value of the dividends beginning in one period and extending out forever

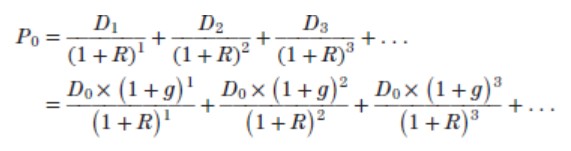
Example: One-Year Holding Period

Considering buying share of equity today, sell it on one year. You will receive:

• Dividend next year = £10

• Sell share next year for £70

• Required return = 25%

• Total future cash: 10 + 70 = £80

Present value = d + FV/ 1+ r

£80 / 1.25 = £64 paid today

General One-Period Formula

let P0 be the current share price, and assign P1 to be the price in one period. D1 is the cash dividend paid at the end of the period

P0​ = D1+ P1​/ 1 + r

• D1​ = dividend next year

• P1 = share price next year

• R = required return​

Infinite Dividend Discount Model

By repeatedly substituting future P₁, P₂, etc., the price simplifies to:

Share value = PV of all future dividends forever.

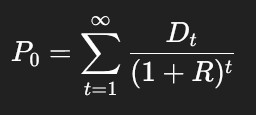
Three Dividend Patterns

We consider 3 special valuation cases:

1. Zero growth (constant dividend)

2. Constant growth (dividend grows at rate g forever)

3. Non-constant growth (supernormal growth then stabilises)

Zero Growth (Constant Dividend)

Dividends = constant forever → a perpetuity.

P0 = D/ R

E.g. Dividend = €10 per year, R = 20%: 10/ 0.20 = £50 P0

Constant Growth (Dividend Growth Model)

Dividends grow at rate g forever:

D1​=D0​(1+g)

Share price today:

P0 = D1/ R - g

Condition: g < R

Constant Growth Example

D0​=£2.30, g=5%, R=13%

D1​=2.30(1.05)=£2.415

P0 = 2.415/ 0.13 - 0.05 —= £30.19

Future Price with Constant Growth

Share price in year t: 

Pt = Dt + 1/ R - g

E.g. Price in year 5 

D5 = D0)1 + g)^5

P5 = D6/ R - g

(where D6=D5(1+g))

When the Constant Growth Model Fails

If g > R

→ Value becomes infinite / formula breaks
Because dividends grow faster than the discounting effect.

Non-Constant Growth (Supernormal Growth)

Dividends grow irregularly for a few years, then settle at constant rate.

Steps:

1. Forecast dividends during high-growth years

2. Compute price at start of constant growth using dividend growth model

3. Discount everything back to today

Non-Constant Growth Example

Company pays no dividends until year 5.
Year 5 dividend = €0.50, grows at 10% forever.
Required return = 20%.

Price in year 4:

P4: 0.50/ 0.20 - 0.10 = £5

P0: 5/ 1.20^4 = £2.41

Non-Constant Growth with Early Dividends

Year 1: €1
Year 2: €2
Year 3: €2.50
After that → constant growth of 5%
Required return = 10%

Price at time 3:

P3: 2.50(1.05)/ 0.10 - 0.05 = £52.50

Present value of:

• Dividends for years 1–3

• Plus discounted P3

P0=€43.88

Two-Stage Growth

Growth rate g₁ for t years → then growth g₂ forever.

Value:

P0​=PV of dividends during stage 1+PV of Pt​

Where:

Pt = Dt + 1/ R - g2

Used when firms have early high growth then long-term stable growth.

Components of Required Return

From the dividend growth model:

R = (D1/ P0) + g

2 components: 

1. Dividend yield D1/ P0 income return from dividends 

2. Capital Gains Yield (g) the growth rate of dividends and share price

Required Return Example

Share price = €20
Dividend next year = €1
Dividend growth = 10%

R: 1/20 + 0.10 = 0.05 + 0.10 = 0.15

Required return is 15%

Verifying Required Return

Price in one year:

P1 = 20(1.10) = 22

Return =
Dividend yield: 1/20=5%
Capital gain: (22−20)/20=10%

Total return = 15%

P/E Ratio

P/E Ratio = share price/ Earnings per share

High P/E → High growth expectations
Low P/E → Slower growth / mature industries

Tech = high P/E
Utilities / mining = low P/E

Notes on P/E Ratios

• P/E ratios fluctuate with market conditions

• COVID-19 caused unusual ratios (price crash → low P/E)

• Can be distorted by very low earnings (denominator effect)