Geometry - Chapter 11

Circumference, area, and volume

*tip: round to the nearest hundredths

when you use the π key on a calculator

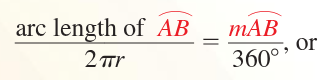
for arc length,

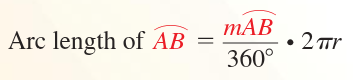
definition for radian

arc length associated with a central angle is proportional to the radius

• radian measure of complete, 360° circle is 2π radians

• circumference of a circle with radius 1 is exactly 2π

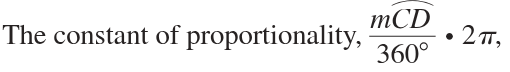
Converting degrees to radians

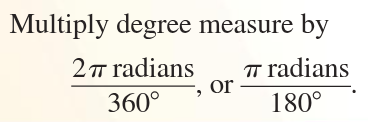
Converting radians to degrees

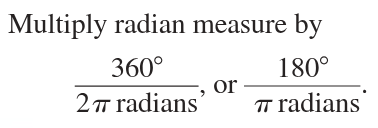
Population density

measure of how many people live within a given area

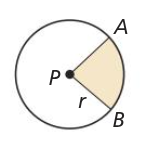
sector of a circle

region bounded by 2 radii of the circle and their intercepted arc

• sector APB is bounded by segment AP, segment BP, and arc AB

To find the area of a sector,

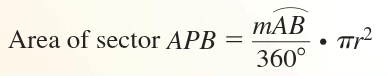
area of a rhombus or kite with diagonals d₁ and d₂ is

½ d₁ ⋅ d₂

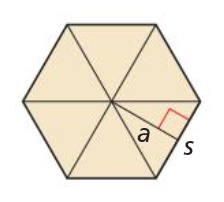
center and radius of a regular polygon are

the center and radius of its circumscribed circle

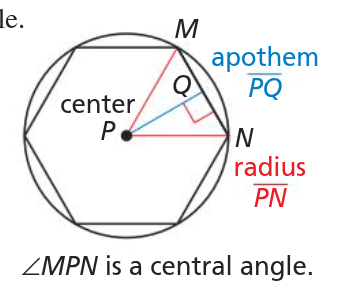
apothem of a regular polygon

distance from the center to any side of a regular polygon

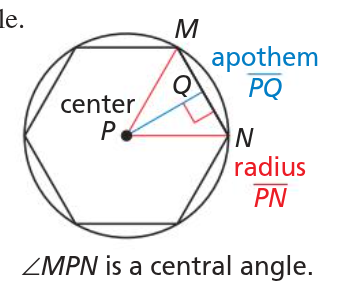
central angle of a regular polygon

formed by 2 radii drawn to consecutive vertices of the polygon

• find by dividing 360° by the # of sides

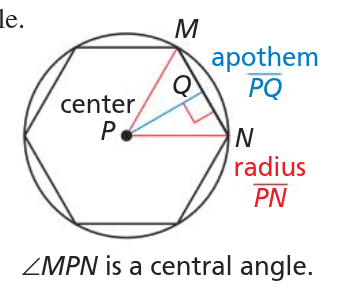
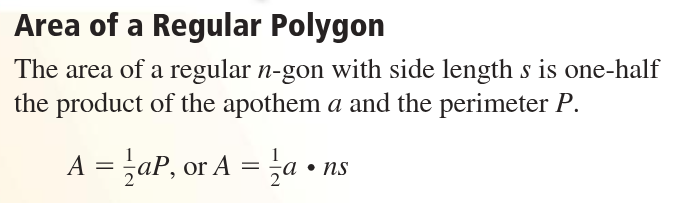
area of a regular n-gon with side length s =

1/2 the product of the apothem a and the perimeter P

• A = ½ a ⋅ P

• A = ½ a ⋅ ns

polyhedron (many sides)

solid bounded by polygons, called faces

• polygons are closed shapes formed by straight line segments

edge of a polyhedron

line segment formed by intersection of 2 faces

vertex of a polyhedron

point where 3 or more edges meet

plural of polyhedron

polyhedra or polyhedrons (can’t have curved lines)

2 bases of a prism are

congruent polygons in parallel planes

base of a pyramid is

a polygon (can’t be a circle - that’s a cone!)

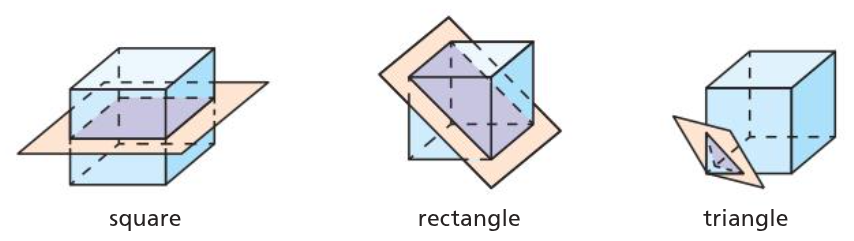
cross section

intersection of the plane & the solid it slices through

solid of revolution

3D figure formed by rotating 2D shape around an axis

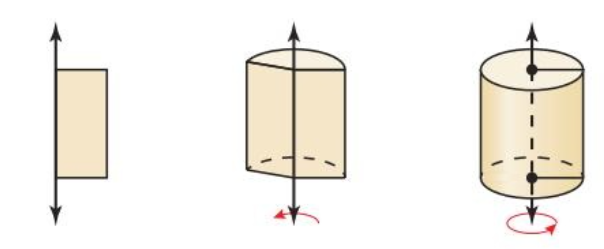
axis of revolution

line around which the shape is rotated

volume

# of cubic units contained in the interior of a solid

Cavalieri’s Principle - if 2 solids have the same height and the same cross-sectional area at every level,

then they have the same volume

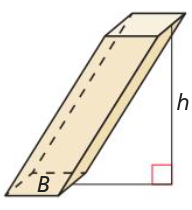
volume of prism

V = Bh

• where B is the area of a base

volume of cylinder

V = Bh = πr²h

• where r is the radius of a base

density

amount of matter that an object has in a given unit of volume

Density

density = mass/volume

similar solids

2 solids of the same type with = ratios for corresponding linear measures, such as heights or radii (called the scale factor)

if 2 similar solids have a scale factor of k,

then the ratio of their volumes is = to k³

Volume of a pyramid

V = 1/3Bh

Area of a sector (lateral area of a cone)

A= πrl

Surface area of a right cone

S=πr²+πrl

• where l is the slant height

Volume of a cone

V=1/3πr²h

great circle

if a plane contains the center of a sphere (intersection)

• separates the sphere into 2 congruent halves called hemispheres

Surface area of a sphere

S=4πr²

Volume of a sphere

V=4/3πr³