Probability Models

Bernoulli Trial Requirements

• There are only 2 possible outcomes (categorized as a success or failure) for each trial

• The probability of success, denoted as p, is the same for each trial

• The trials are independent

10% Condition

Overrides the violation of independence assumption by sampling without replacement as long as not more than 10% of the population is not sampled (probabilities would not change too much)

Geometric Model

Probability Model used to see how long it will take to achieve the first success in a series of Bernoulli Trials; denoted Geom(p)

Geometric Model Formula

P(X=x) =q^x-1 *p

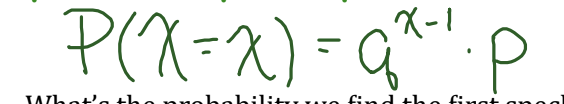
Expected value Formula (Geometric)

E(x)= μ: =1/p

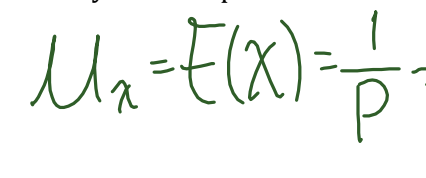
Standard Deviation Formula (Geometric)

σ=sqr(q/p²)

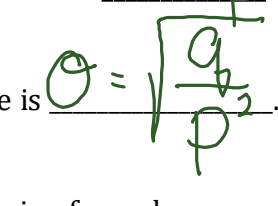
Binomial Model

The probability model used when trying to find the # of successes in a specified # of trials (want to find P(X=#); denoted as Binom (n,p)

Difference b/w Geometric and Binomial

In a Geometric model, a sample size isnt given, while a Binomial model does

There are many different __ to get a specific # of successes in a specific # of trials

COMBINATONS

Combination

Each different order we have k successes in n trials

Combination formula

(n k) = n!/k!(n-k)!

Mean Formula (Binomial)

μ= np

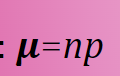
Standard Deviation Formula (Binomial)

σ= sqr(npq)

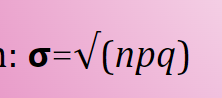
Probability Formula (Binomial)

P(X=x)= (n x) p^x q^n-x

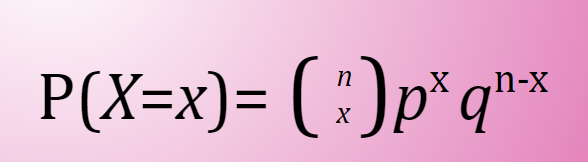
A sample size being LARGE ENOUGH depends on..

the probability of success (the smaller the probability of success (or larger/small q), the larger sample size needed

Success/Failure Condition

States that a Binomial model is approx. Normal if we expect at least 10 successes and 10 failures (np > or = 10 and nq > or =10)

Statistically Significant

When the results of an experiment or a sample are not reasonable to believe they occurred just by chance (Use Binomial/ Normal Model if Bernoulli Trials and Success/Failure Conditions are met)

What Can go Wrong?

• Before using any probability model, make sure that you have Bernoulli Trials

• Don’t confuse Geometric and Binomial Models

• Don’t use Normal Model approx. with a small end

Parameters of Probability Models

p= Probability of success

q (aka 1-p) = Probability of failure

x= number of success in n trials (binomial) or number of trials until first success (geometric)

n= number of trials (binomial)