Biostatistics exam 3 - Multiple Explanatory Variables

Generalizing linear models

• in a linear model the null hypothesis is β = 0

• so setting β = 0 reduces the equation

Y = α + βX → Y = α'

• α' =constant that equals the grand mean

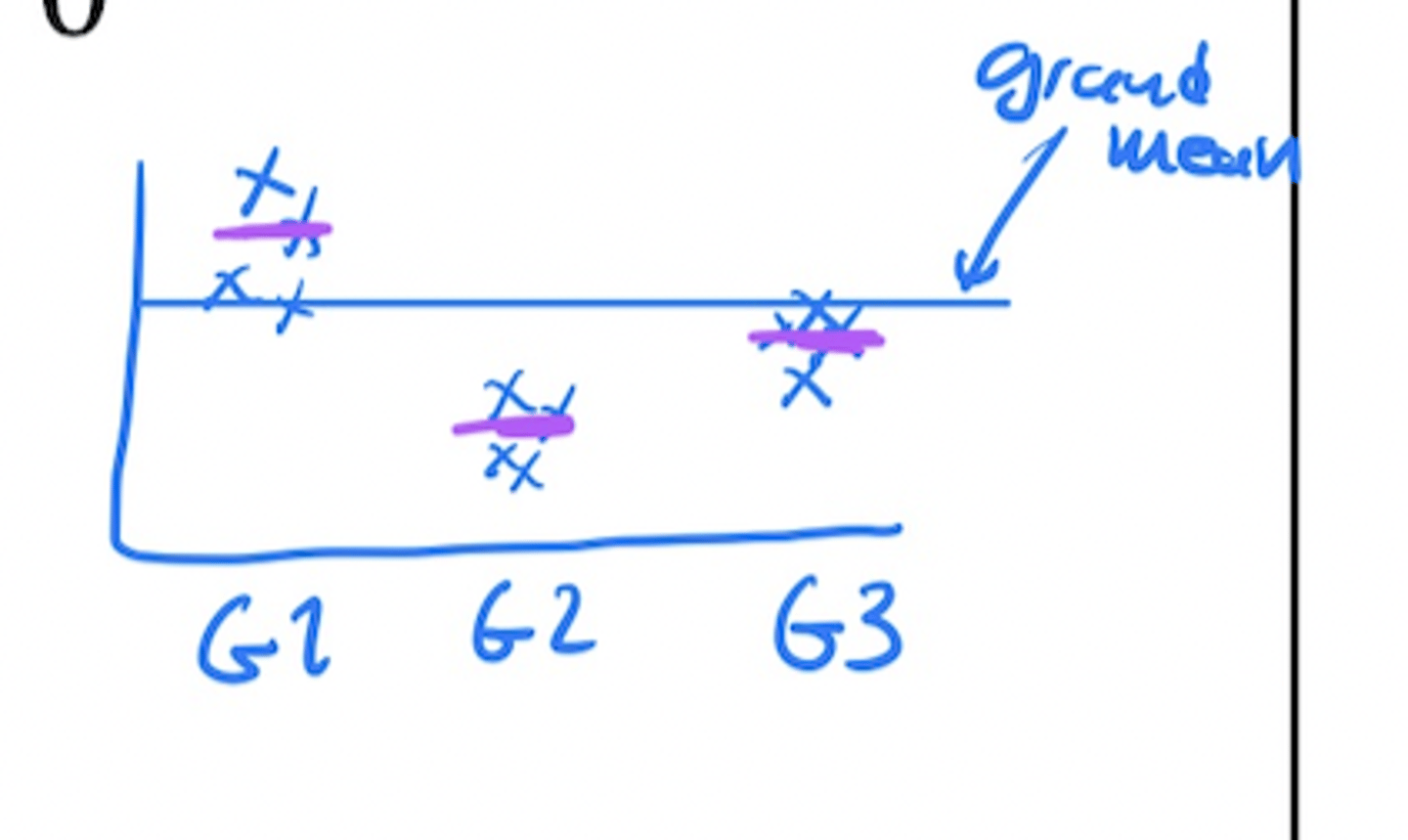
Is ANOVA a linear model?

YES

ANOVA as a linear model (equation)

Linear model: Y = µ + A

• Y: response

• µ: grand mean (constant)

• A: treatment

Example: circadian clock study: shift = constant + treatment

hypotheses for ANOVA linear model

H₀: Y (response) = Grand mean (constant)

Ha: Y (response) = Grand mean (constant) + Treatment

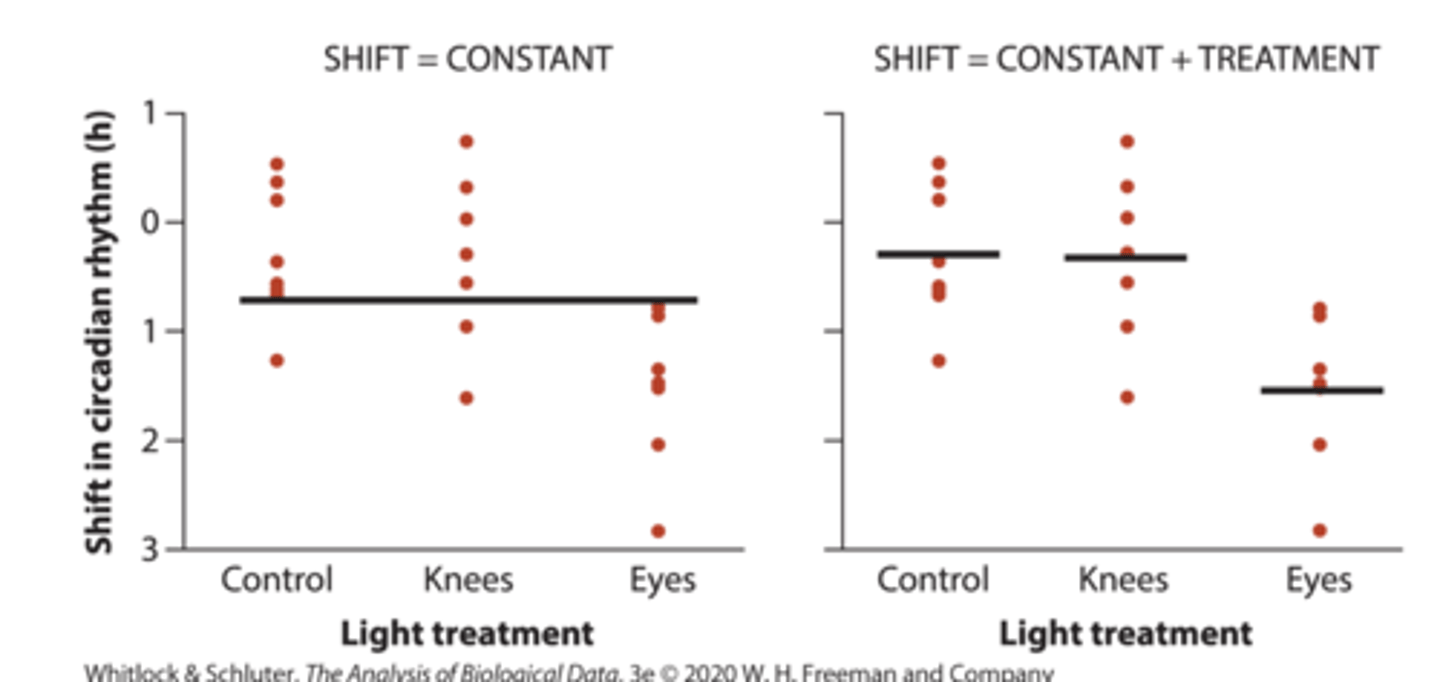
sampling error for ANOVA as a linear model

Even if the hypothesis is true, however, the treatment means will be different due to sampling error thus, the full model with treatment will be a better fit to the data

** F-ratio takes this into account

F-ratio for ANOVA as a linear model

F-ratio is used to test whether including the treatment variable in the data results in a significant Improvement in the fit of the model to the data

• compared with the fit of the null model lacking the treatment variable

ANOVA linear model for multiple explanatory variables (equation)

Response = constant + explanatory

• extending for multiple explanatory variables

Response = constant + exp1 + exp2 +...

• models often include an interaction term

Response = constant + exp1 + exp2 + exp1 * exp2

• design is called a two-way ANOVA or two-factor ANOVA

interaction term

Means that the effects of one variable on the response depends on the value of the second variable

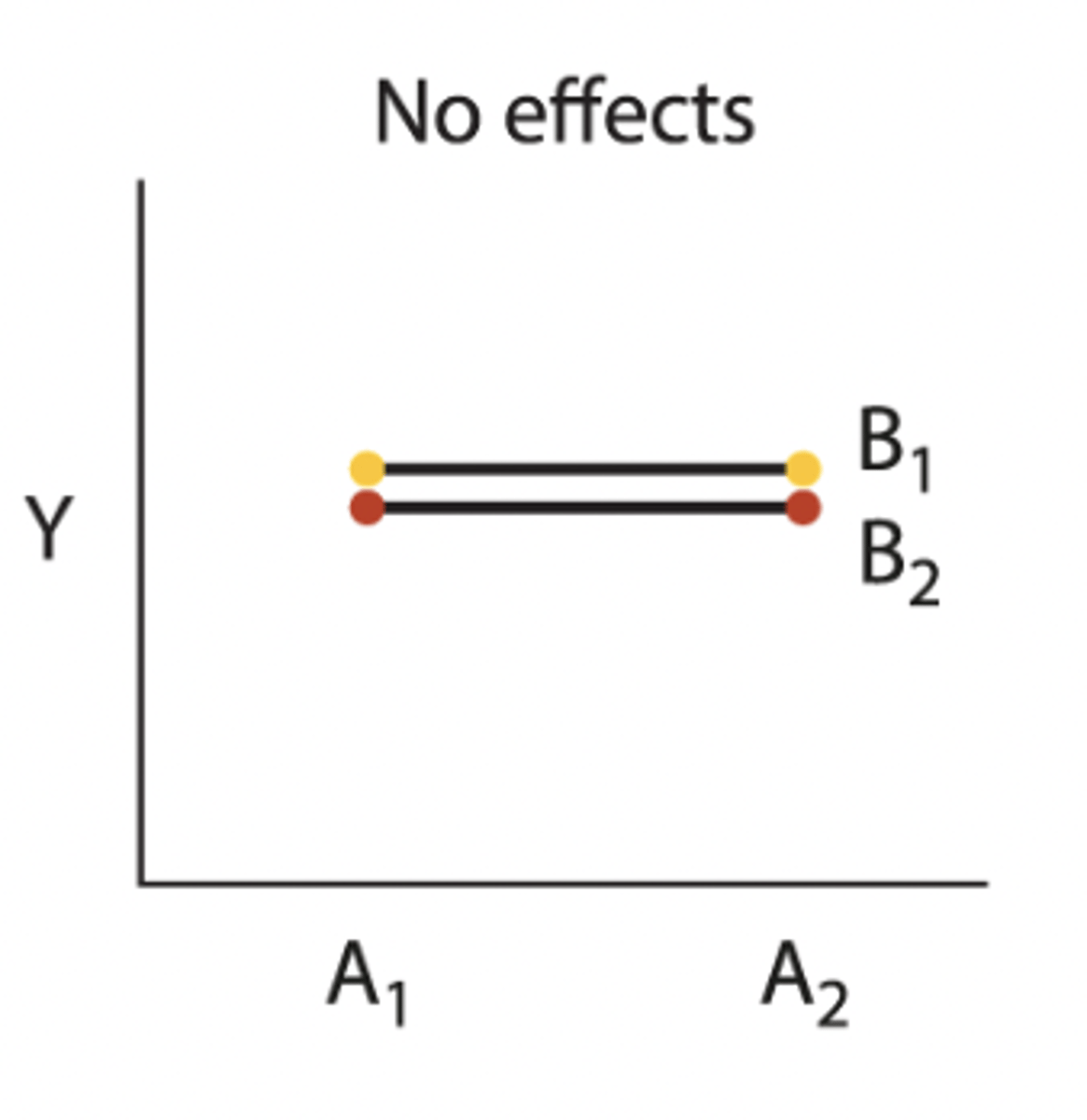
Two - factor outcome (no effect)

• no difference in averages for A or B

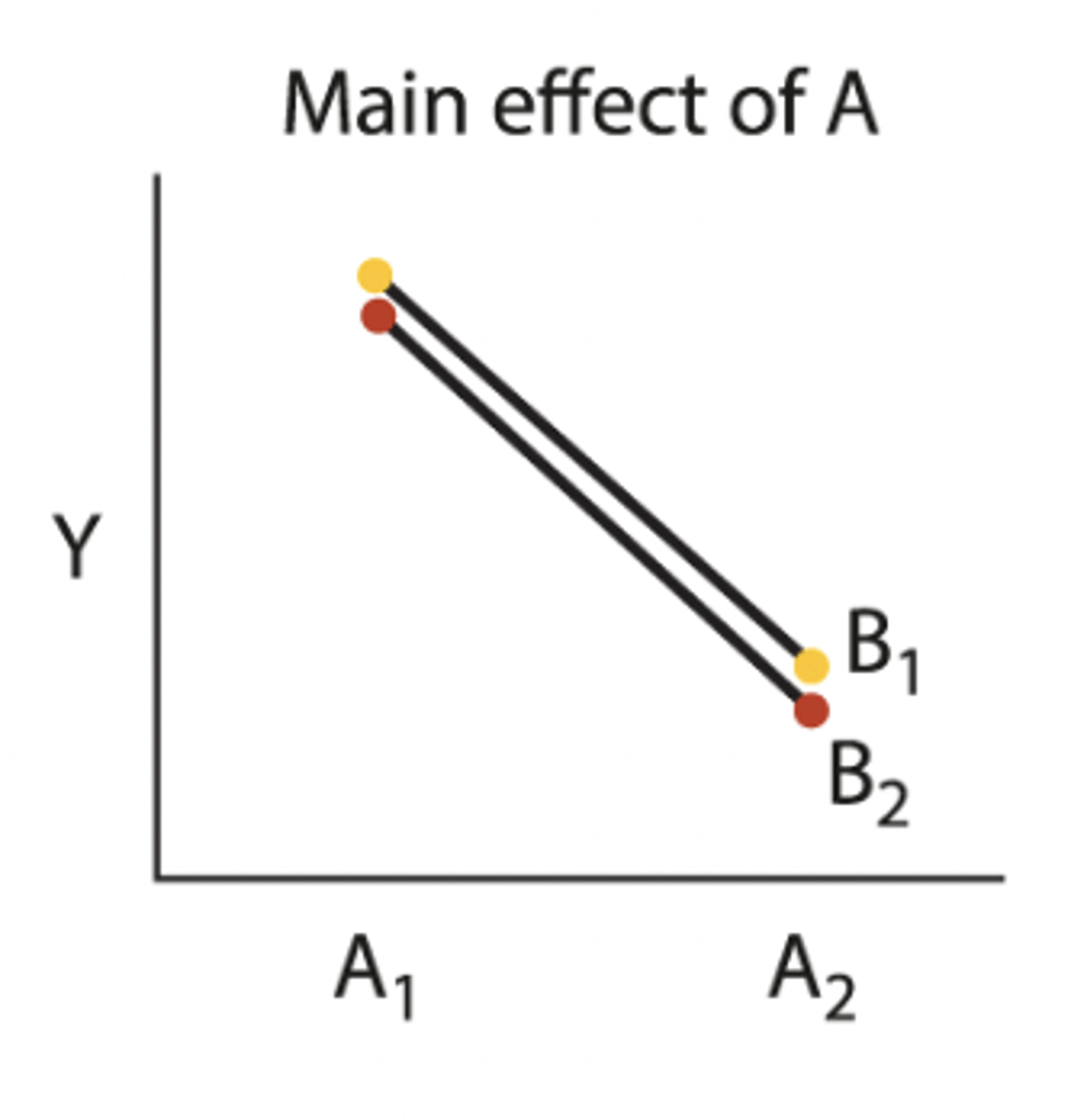
Two - factor outcome (Main effect of A)

• average of A1 and A2 are not the same (A effect)

•average between the two yellow dots is the same as the average between the two red dots (No B effect)

Two - factor outcome (Main effect of B)

• A1 and A2 avg is the same (no effect of A)

• average of two yellow dots will be higher than the average of the two red dots Different Y-ints

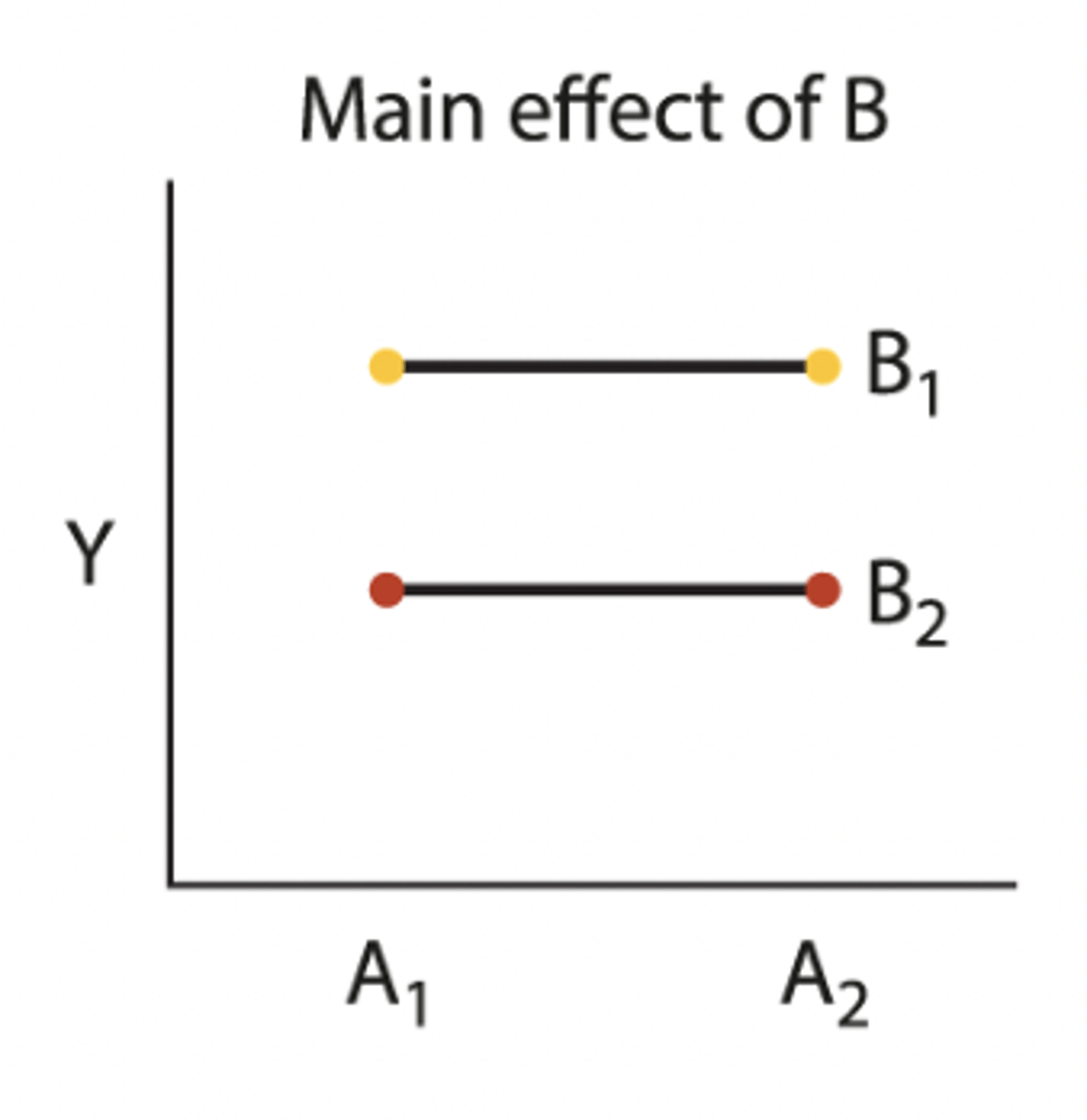
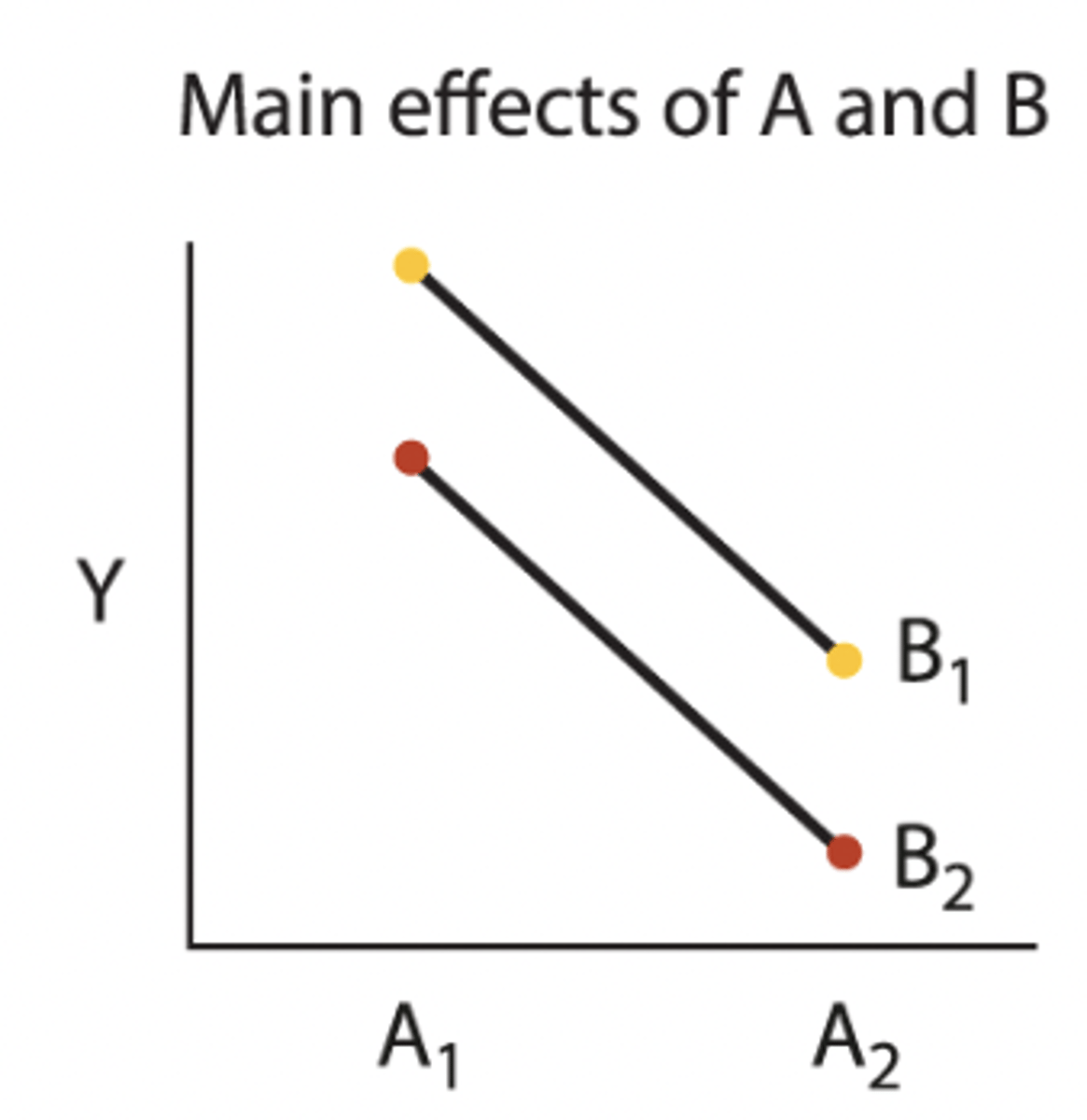
Two - factor outcome (Main effects of A and B)

• A1 and A2 average is not the same (A effect)

• The average of two yellow dots is higher than red, so B has an effect (DIF Y-INT!)

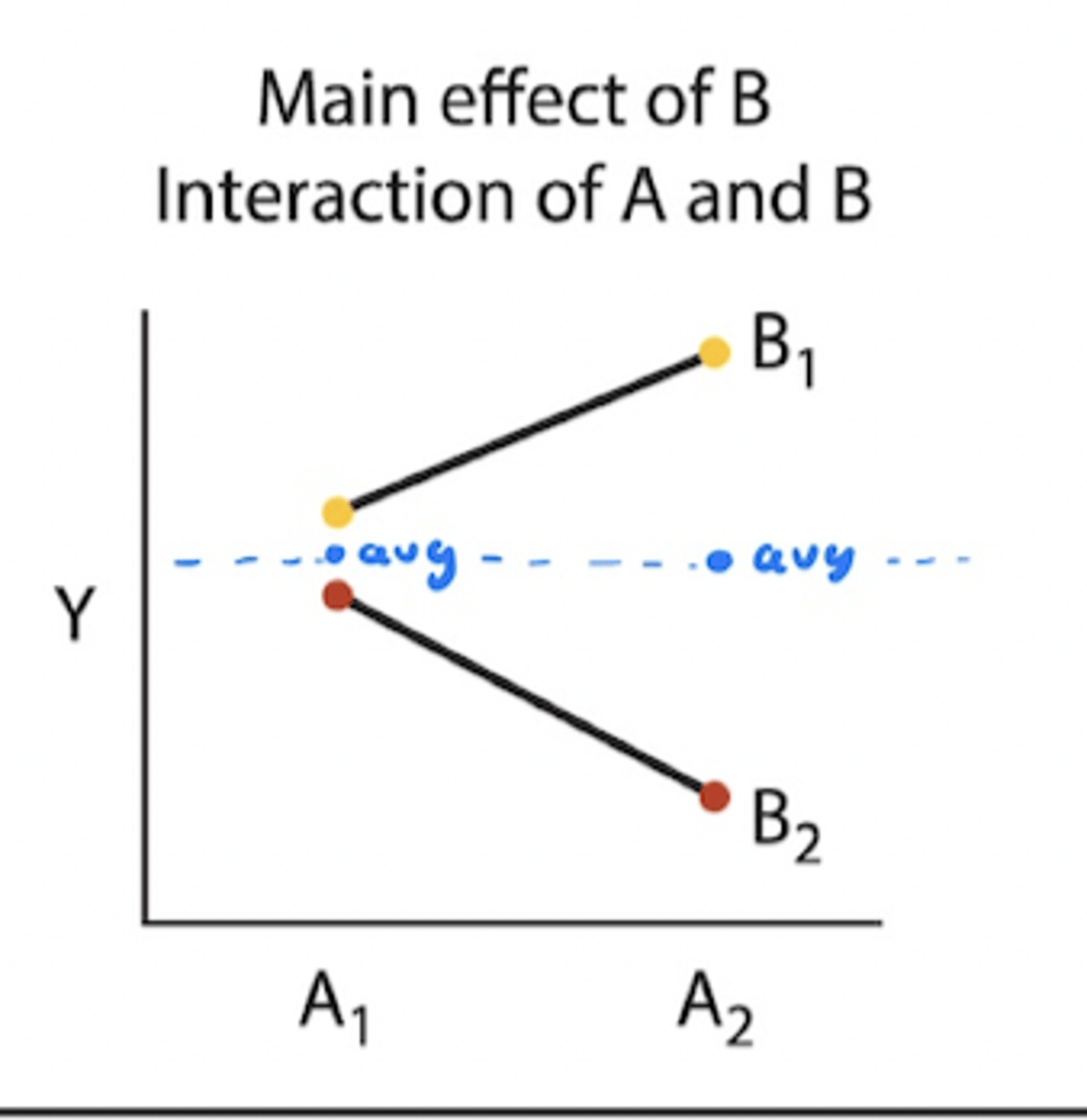
Two - factor outcome (Main effect of B with interaction of A and B)

• A1 and A2 average is the same (No main A effect)

• average of yellow is higher than red (B main effect)

• what happens with B depends on A (diff slopes -> interaction between A and B)

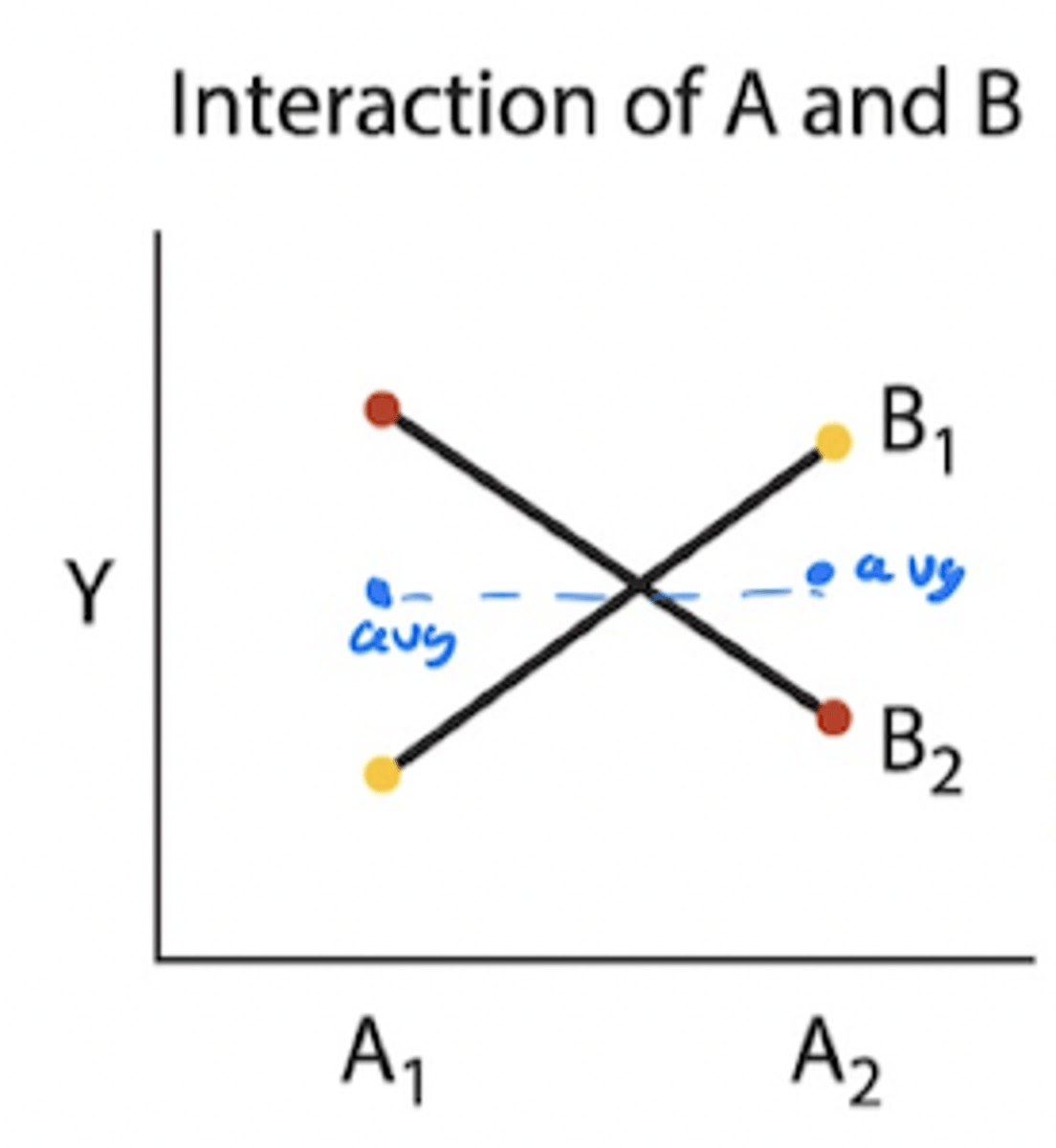
Two - factor outcome (Interaction of A and B)

• different slopes (Intraction)

• average A1 and A2 are the same (No main effect of A)

• average of yellow dots and red dots are the same (no main effect of B)

Assumptions of two-factor ANOVA linear models

• the measurements at every combination of values for the explanatory variables are a random sample from the population of possible measurements

• the measurements for every combination of values for the explanatory variables have a normal distribution in the corresponding population

• the variance of the response variable is the same for all combinations of explanatory variables