AP CALC Mass Set

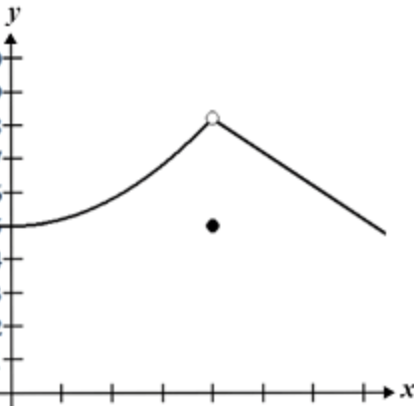
removable discontinuity

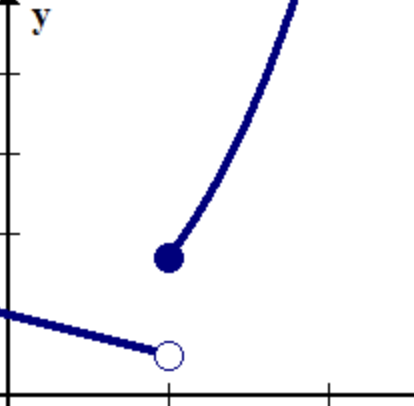
jump discontinuity

pythagorean identity

sin²x + cos²x = 1

chain rule

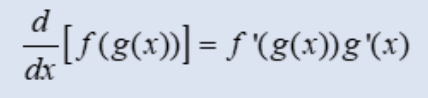
Intermediate Value Theorem (IVT) conditions

guarantees that a point exists in between two numbers on f(x)

1. must be a continuous function

2. must be a number between f(a) and f(b)

Extreme Value Theorem (EVT) conditions

guarantees that f(x) has an absolute minimum or maximum on an interval

1. must be continuous

2. must be on a closed interval [a,b]

Mean Value Theorem (MVT) conditions

guarantees at least one point where Instantaneous RoC is equal to Average RoC

1. must be differentiable (proves continuity)

First Derivative Test

used for finding relative min/max

1. identify critical points

2. sign chart

3. write conclusion

Candidates Test

used for finding absolute min/max

1. identify critical points

2. list critical points and endpoints in a table

3. evaluate f(x) at those values

4. write conclusion

Point of Inflection

when f’’= 0 and changes concavity, and when f’ has extrema and changes signs

1 over 0

undefined

0 over 1

0

Second Derivative Test

if f’(a) = 0 and f’’(a) is negative = relative max, positive = relative min

Optimization

use with words like minimize/maximize

1. write equation for the optimized quantity

2. write equation for the constraining variable

3. rewrite equations in terms of one variable and combine

4. use Candidates Test to find extrema

5. interpret the answer in context

derivative of sin(x)

cos(x)

derivative of cos(x)

-sin(x)

f(x) is concave up

f’(x) is increasing and f’’(x)>0

f(x) is concave down

f’(x) is decreasing and f’’(x)<0

f(x) has a point of inflection

f’(x) has relative extrema and f’’(x) = 0

implicitly derive xy