Ch 2 - Modeling Distributions of Data

percentile definition

the value with p percent of the observations less than or equal to it (“at” not “in)

percentile sentence template

• ___ is at the pth percentile

• p% of data points (units) were less than/greater than or equal to____

(general = less than, specific = greater than)

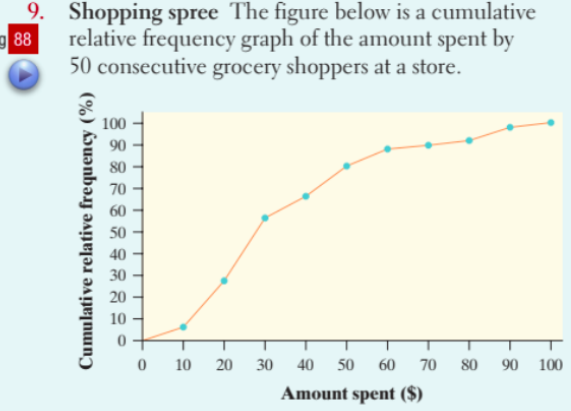
cumulative relative frequency

a graph showing the accumulation of frequencies up to each category in a dataset, allowing comparison of different percentiles.

z score

how many standard deviations from the mean & observation falls & whether it is above (pos.) or below (neg.) the mean

• also known as the standardized score

z score formula

data item - mean / standard deviation

z score sentence template

The “data item” is “absolute value of z-score” standard deviations above/below the mean.

measures of center & location

• mean, median, quartiles

measures of spread

• standard deviation, range, IQR

transforming data with addition or subtraction (of constant a)

• center & location (mean, median, quartiles, max, min) change by a

• spread (standard deviation, range, IQR) and shape stay the same

• Z SCORE DOESNT CHANGE (bc total stand devs)

bc the pts are still the same relative to each other (horizontal/vertical shift)

transforming data w/ a multiplier (of constant b)

• center & location (mean, median, quartiles) shrink/stretch by b

• spread (standard deviation, range, IQR) shrink/stretch by b

• shape does not change

• Z SCORE DOESNT CHANGE (bc total stand devs)

bc this is a stretch/shrink it zooms in/out the graph

μ

mean :)

M

population mean (to do w/ normal curve)

x bar

sample mean

σ

standard deviation :)

a density curve

the smooth curve drawn thru the tops of HISTOGRAM bars (2 characteristics)

• is always on or above the horizontal axis

• has TOTAL area exactly 1 underneath it

(no set of real data can be exactly described by density curve, curve is an approximation)

• does not matter on a continuous x axis if x=# bc if it equals its a vertical line ~ 0 

median of a density curve

equal area point where half the area under the curve lies to the left and half to the right, representing the middle value of the distribution.

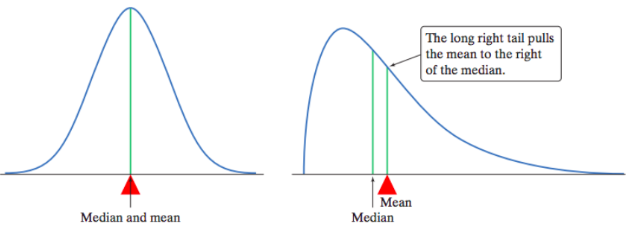
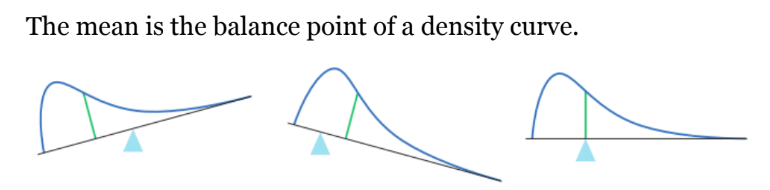
mean of a density curve

balance point of a density curve (the center of gravity of the distribution, not necessarily where the areas are equal.

• Skew pulls the mean toward the longer tail.

proportion probability

4 things

1. [0,1] bc def of density curve

2. P(x>#) = x(height) = .decimal area

3. =%

4. UNITS

P(point = x)

is about 0 bc is a vertical line

Normal Distributions

“special” type of density curve

• notation: Normal

• same overall shape: symmetric, unimodal, and bell-shaped

(not all symmetric curves are normal, ie bimodal)

Describing normal distribution

Must identify 2 things:

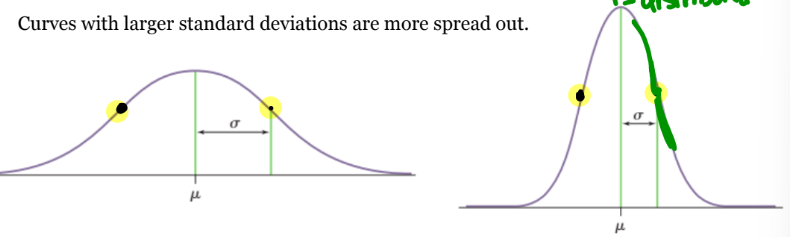
• mean μ→ the center (bc symmetric)

• standard deviation σ → is the dis. from the center to the change-of curvature points on either side (points of inflection)

  • 1 standard dev. above mean, 1 standard dev. below

• larger stand dev = more spread

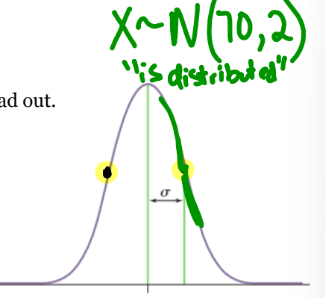
normal distribution notation

uses N(µ, σ), where µ is the mean and σ is the standard deviation

• X ~ N (70,2)

• “x is distributed” on normal curve mean of 70, standard deviation of 2

any Normal curve “standardized” =

N(0,1)

converting this to z score

• mean: 0

• standard deviation: 1

STANDARDIZING DOES NOT CHANGE the overall shape of the distribution.

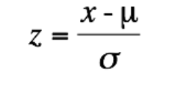
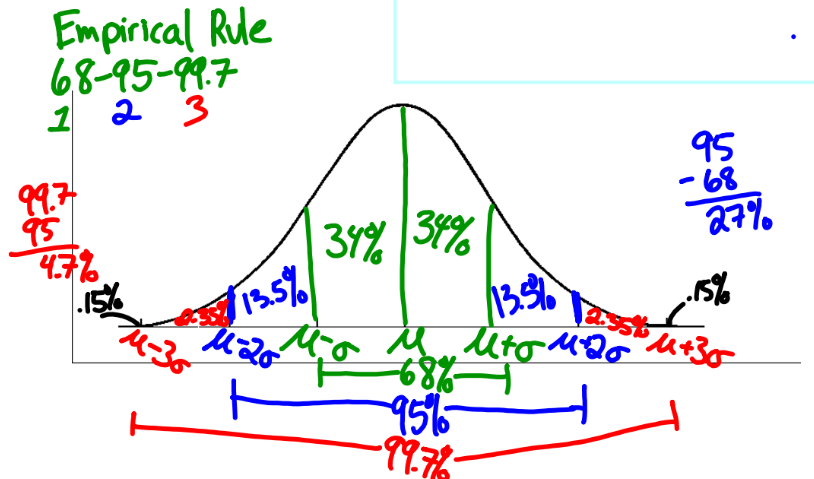
Empirical Rule

68-95-99.7 rule

• appx. 68% of area falls within σ of the mean µ

  • if the curve is symmetric & normal

  • (1 stand below mean - 1 stand dev above mean)

• appx. 95% of area falls within 2σ of the mean µ

  • (2 stand below mean - 2 stand dev above mean)

• appx. 99.7% of the area falls within 3σ of the mean µ

  • (3 stand below mean - 3 stand dev above mean)

.15%, 2.35%, 13.5%, 34%, 34%, 13.5%, 2.35%, .15%

f(μ) of a normal curve

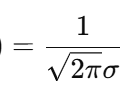
steps to proportion when z score is not integer

1. draw normal curve and shade area of interest

2. use proper notation to write proportion of interest p(z < #) = proportion of area to left of z score

3. (if u use a diff variable u must define it and x~N(115,6) before converting to z score

Is the data normal?

Make a Normal Probability Plot (which assumes data is normal)

• enter data

• → stat plot

• → select graph

• → zoom 9

“The Normal Probability Plot is roughly linear so the data is approximately Normal”

if its asks abt a percentile, proportion or percent its asking for?

area!

if it asks abt a data item, mean, or standard deviation?

find z score! go backwards

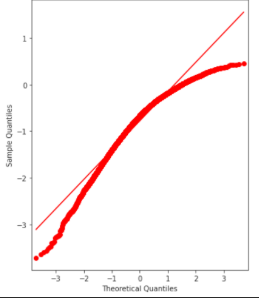
normal probability plot ∩

majority of data points falls on the right side (of the linear line), which indicates a tail on the left, so the data is skewed left

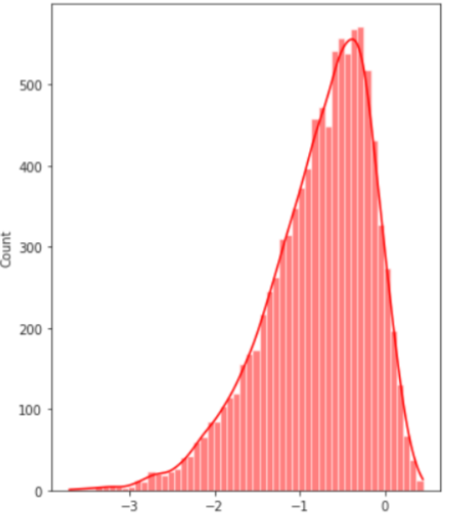
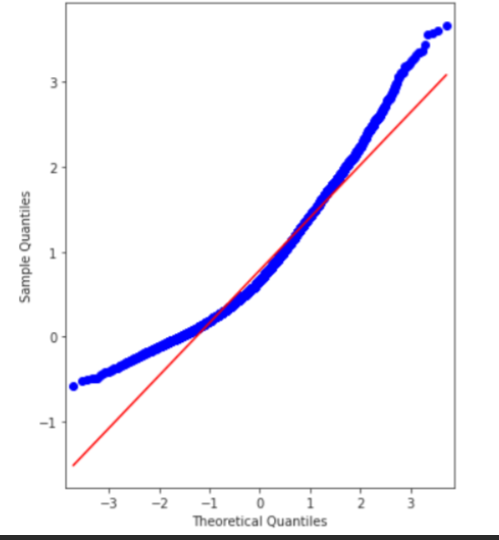
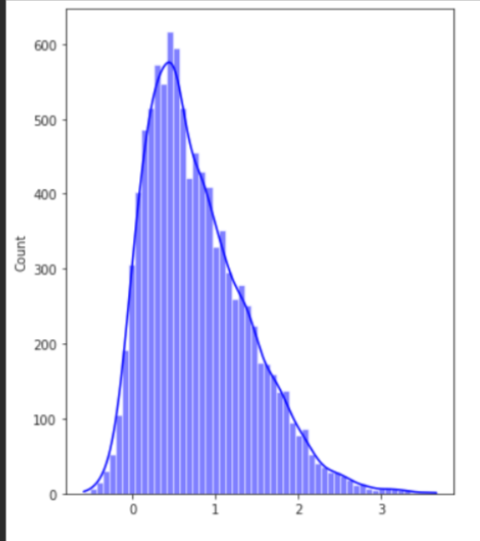
normal probability plot ∪

majority of data points falls on the left side (of the linear line), which indicates a tail on the right, so the data is skewed right

when changing the paramenters of a Normal curve?

restate the distribution