Module 4: Multiple Regression

Main advantage of using multiple regression over correlation

The ability to test the association of multiple predictors and a criterion variable.

What can multiple regressions test?

• Whether the predictors are significantly associated with the criterion as a group

• Whether individual predictors are associated with the criterion when we account for overlap between the predictor variables themselves

  • I.e. Isolating the variables

Bivariate regression analysis

Form of multiple regression where there is a single predictor

Multiple regression assumes your variables are measured on a _________ scale.

continuous

While you can use categorical predictor variables the criterion must be…

continuous

What should you do if you have a categorical variable in a multiple regression?

Code it to make it continuous

Think: Variable is attendance, we are interested in perfect vs non-perfect attendance, therefore we can dummy code it by giving non-perfect a value of 0 and perfect a value of 1.

Formula for multiple regressions

Y’ = b0 + b1X1 + b2X2 + b3X3…

Where each bX is a predictor variable

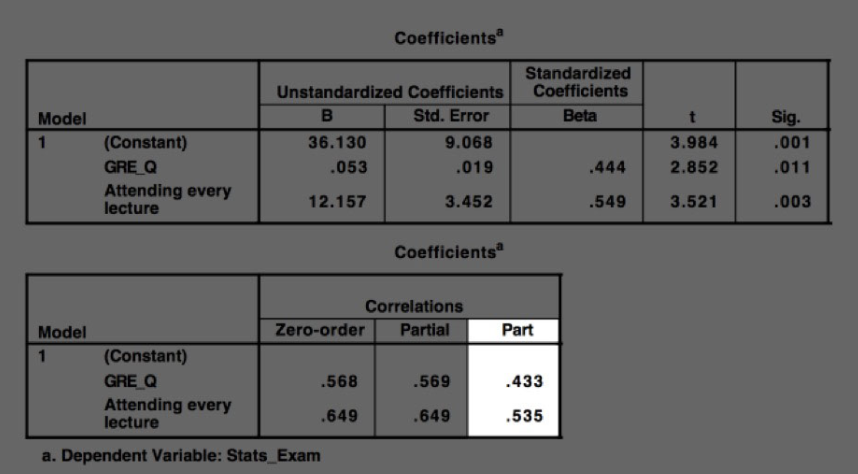
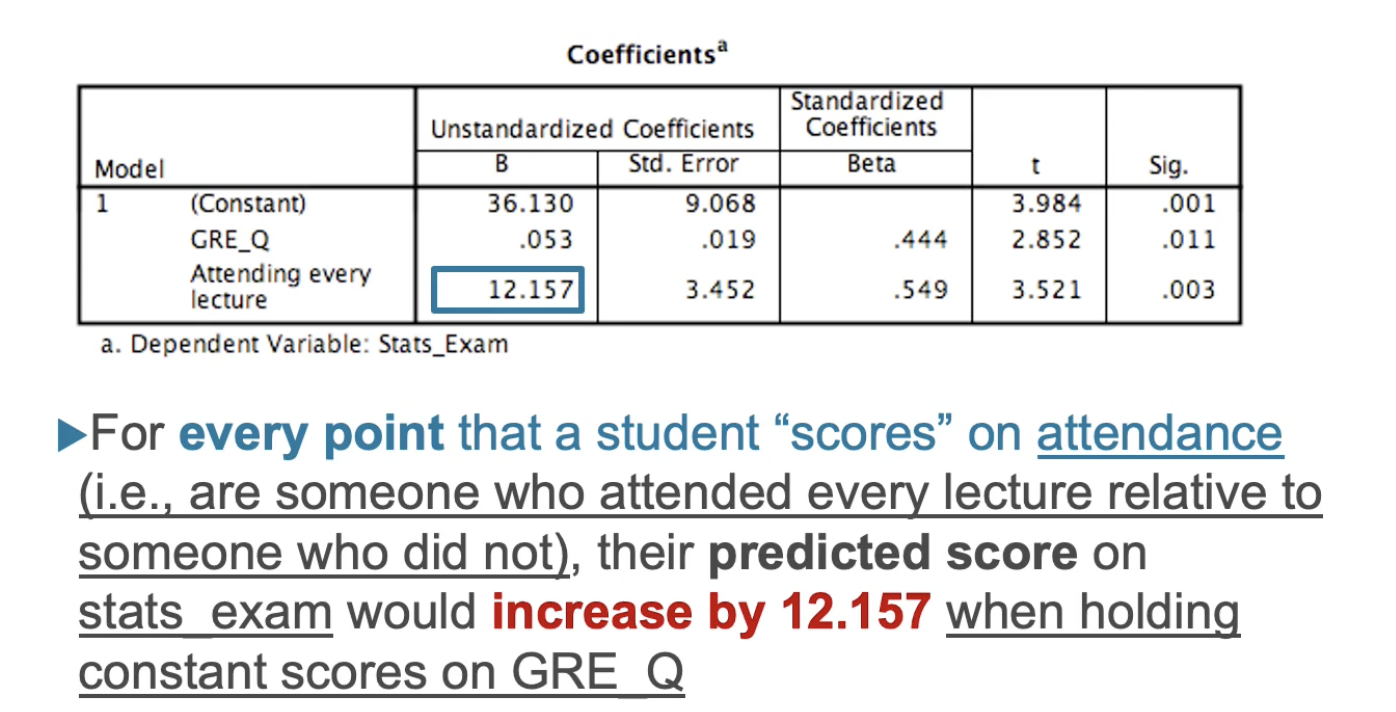
Unstandardised Coefficients for the intercept and slopes are based on…

The metric of the variable

• The relevant unit of measurement for the variable

Think: CM, test score, attitude score, frequency of occurrence, etc

Limitation of using unstandardised coefficients in multiple regressions

You can’t tell which predictor variable is the ‘better’ one with the most predictive value

• It’s like comparing apples and oranges, or a test scored out of 80 vs out of 200.

• Think: If you score 100% on both tests, the score for the out of 80 will always be lower.

Why do we use standardised coefficients in multiple regressions?

It converts measures of all variables to a common unit to make comparisons.

In the case of the multiple regression analysis the test of significance refers to…

The association between each predictor and controlling for the other predictor variables. 

What does the significance value in the ANOVA table tell us?

The significance of the total model

• The significance of the combined effect of all predictors

• Significance of R

What do the significance values in the coefficients table tell us?

The significance of each predictor, controlling for combined effects of other variables (isolating the predictor variable of interest)

• The significance of the bivariate correlation

• The significance of r

Where can the value of R be found and what does it mean?

It is the combined effect of all the predictor variables on the criterion.

• Model summary table

• Interpreted as a correlation

What does R Square in the model summary table tell us?

The amount of variance accounted for by the predictors (combined).

• % variance in response variable (criterion) explained by variables a b and c.

Unique Variance

Variance that is unique to each predictor

• Independent of any other predictor

• Think: Isolating the variable

Explain multiple regressions in the analogy of a group assignment

Criterion: Grade for assignment

Predictor Variables: Effort of Individual Group Members

You would use R, R squared and the significance to see if the group as a whole was predictive of the grade received on the assignment.

You would use r, r squared and the significance to see how much each individual’s effort explained the grade.

Looking at R, you might see that the group effort as a whole explained 90% of the grade (we could say that 10% was explained by the fact that it was a difficult subject)

If you look at r, you might see that one person accounted for 80% of that model and the others slacked off.

Therefore you would interpret this as, the entire model (group) was significantly predictive of the grade, but person A accounted for most of this.

How do you get the unique variance of each predictor variable?

Square the ‘part correlation’ values in the SPSS output.

• Can convert it into a % of variance explained

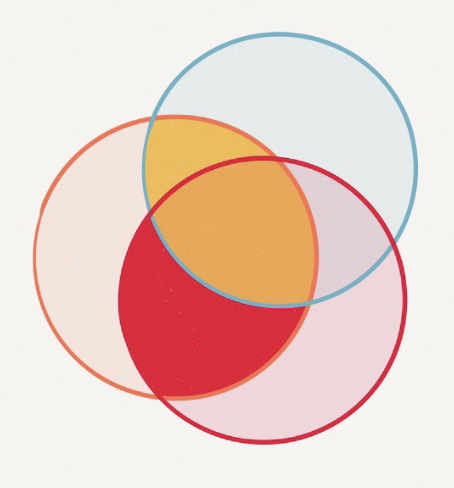
If the criterion is the orange circle, the unique variance of predictor 1 with the criterion is shaded…

Yellow/red

If the criterion is the orange circle, the unique variance of predictor 2 with the criterion is shaded…

Yellow/red

If the criterion is the orange circle, the shared variance of predictors 1 and 2 with the criterion is shaded…

Orange

Multicollinearity

When predictor variables have very high correlations with each other

In a multiple regression, b-weights are referred to as…

Partial slopes

• Each b-weight tells us how much change in Y’ for each unit change in that variable when all other variables are held constant.

Think: In the equation there are multiple slopes (b1’s) because there is one for each predictor variable

Think: In the equation/formula itself, b1X1 forms the slope, and b1 (the b-weight) forms part of the slope

Linear Composite

The regression equation (model)

H₀

The null hypothesis

• There is no linear relationship between X and Y in the population

H₁

Alternative hypothesis

• There is a linear relationship between X and Y in the population

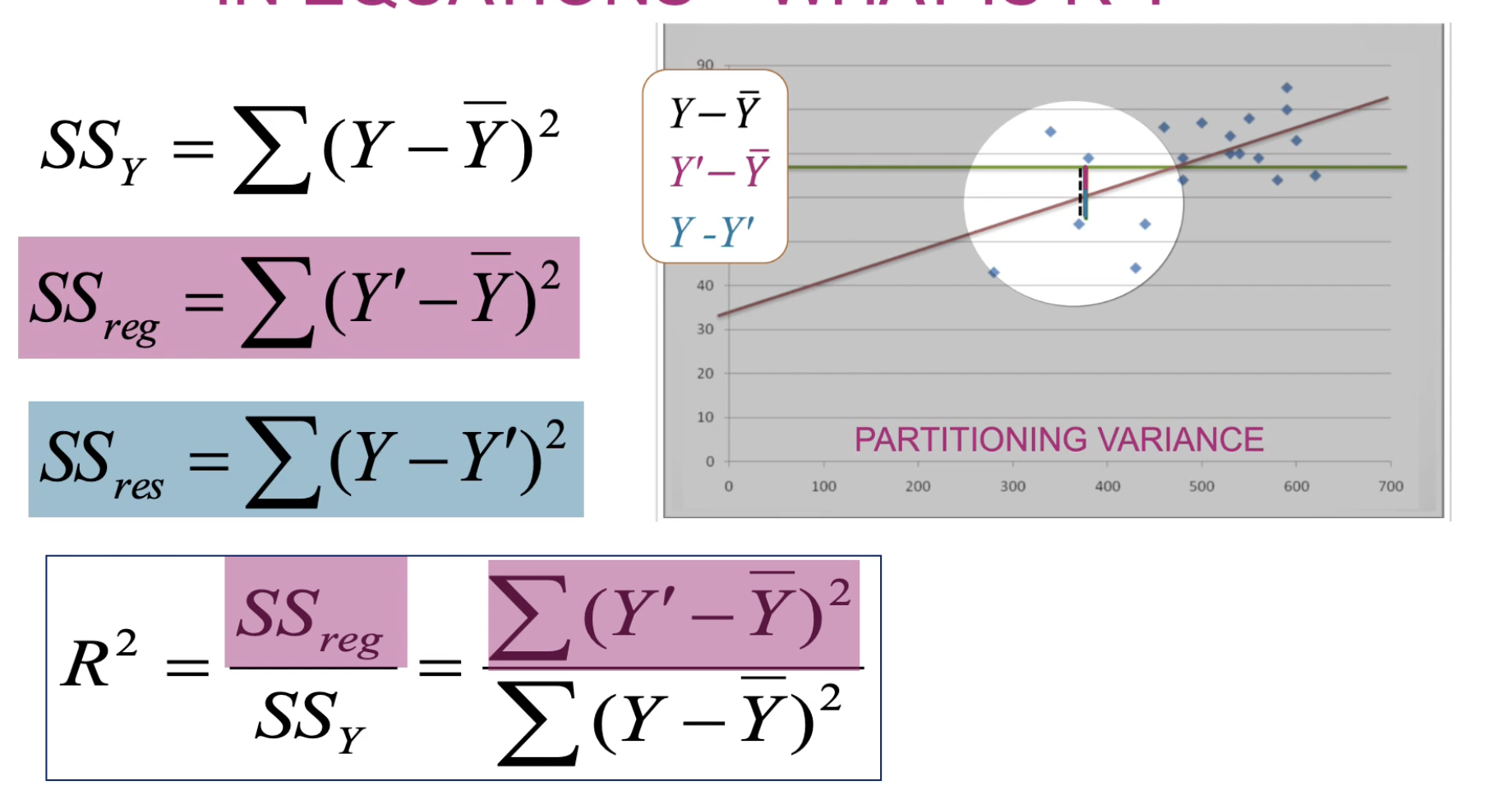
R square formula

Gives variance explained by the model

Semipartial Correlations

Measures the unique relationship between one independent variable and the dependent variable, while controlling for the influence of other independent variables.

• Square to get proportion % of accounted variance by that variable

• Under ‘part’ column in SPSS

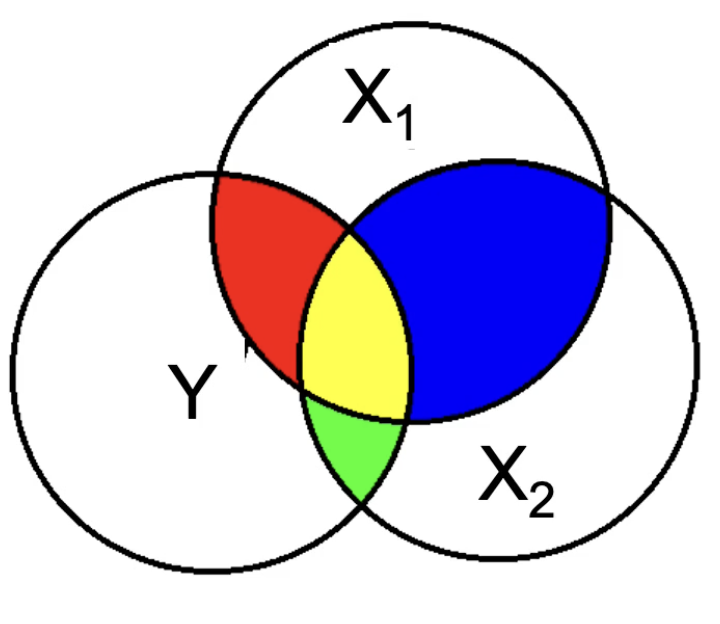
What does the blue represent?

Unique variance that is not accounted for by the model at all.

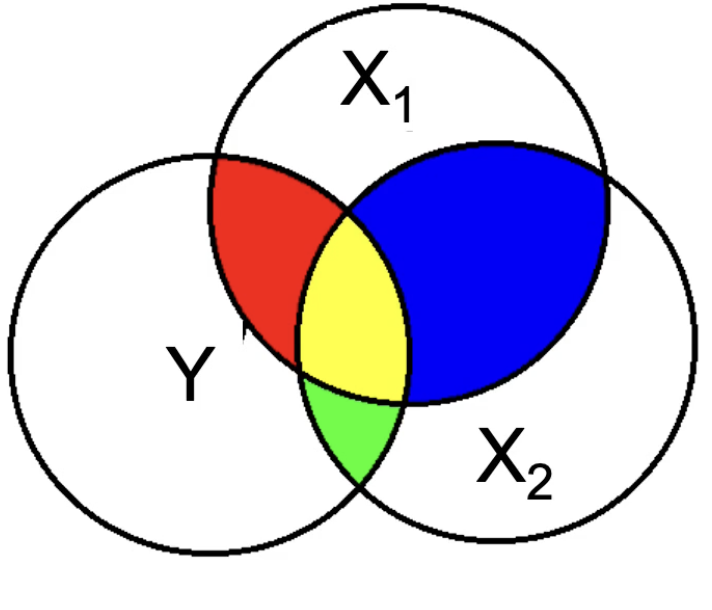
Which colours represent unique variance?

Red and green

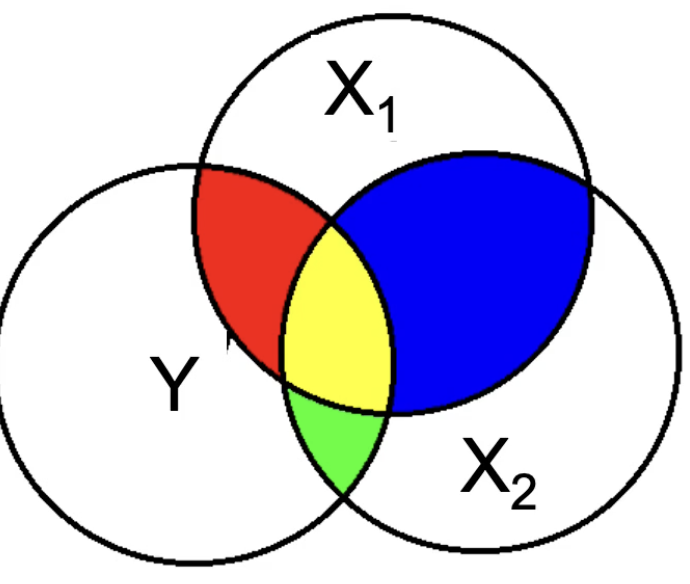
What does yellow represent?

The shared effect

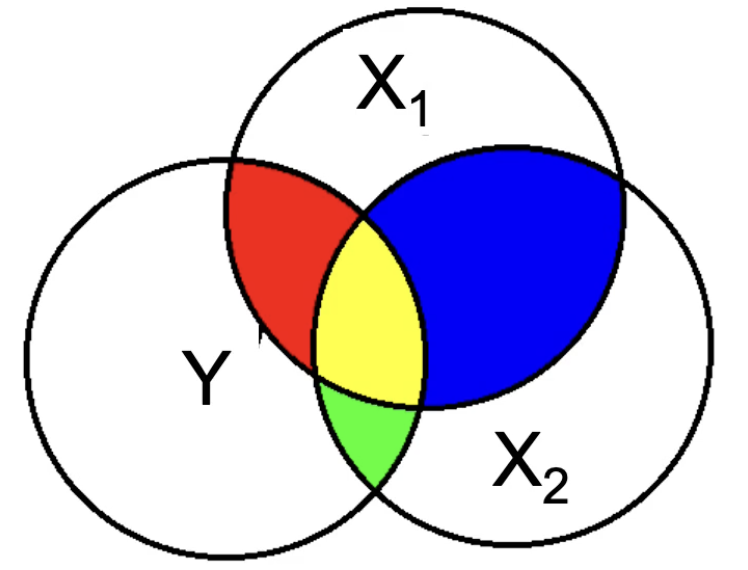
What do the red, green and yellow sections combine represent?

R squared

Any correlation value squared gives you…

Proportion of variance explained

Shared variance refers to

Combined effects of predictor variance on criterion