Stuff to Know Cold for AP Precalculus

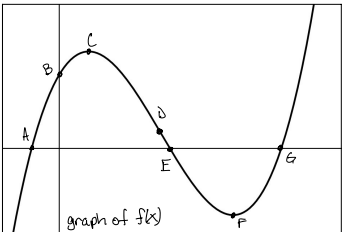
concavity and rate of change from (-∞, D)

concave down, decreasing

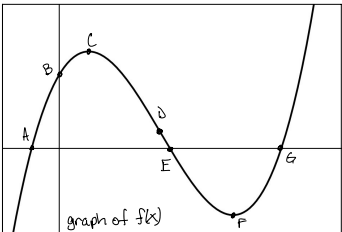
concavity and rate of change from (D, ∞)

concave up, increasing

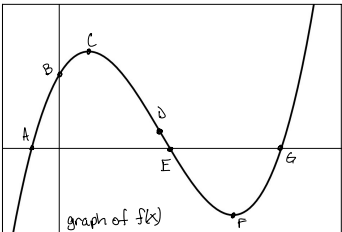
Describe f(x) on the interval (C, F)

function is decreasing and the rate of change is negative

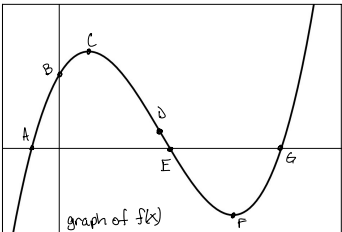
Describe f(x) on the interval (F, ∞)

function is increasing and the rate of change is positive

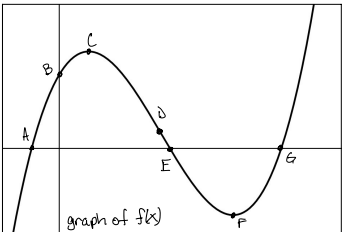
Is the function positive or negative on the interval (A, E)?

positive

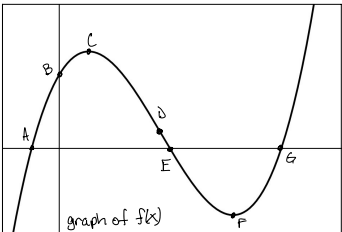
Is the function positive or negative on the interval (E, G)?

negative

Describe change patterns in a linear function.

rate of change is constant on any interval

Describe change patterns in a quadratic function.

the 2nd differences are constant over equal length input intervals

Describe change patterns in a polynomial function with degree n.

nth differences of output values are constant over equal length input intervals

Describe change patterns in an exponential function.

output values are proportional over equal length input intervals

Describe change patterns in a logarithmic function.

proportional input values result in constant change in output values

What is the average rate of change of f(x) over the interval [A, B]?

slope of the line between the points

f(b) - f(a)/b-a

What is rate of change?

refers to slope AT THAT POINT

verbalize this

As the input value increases without bound, the output value approaches 3. (graph has a horizontal asymptote at y = 3)

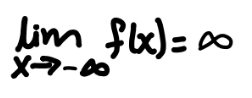
verbalize this

As the input values decrease without bound, the output values increase without bound.

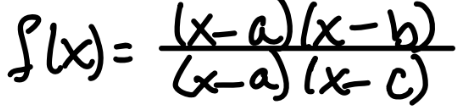
f(a) —>

0/0 (hole)

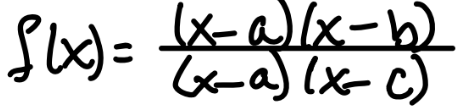
f(b) —>

#/0 (x-intercept)

f(c ) —>

0/# (VERTICAL asymptote)

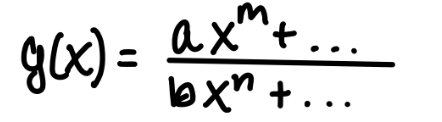
if m < n

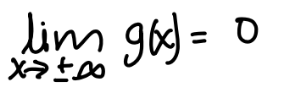
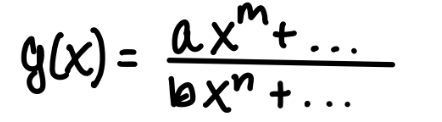
if m = n

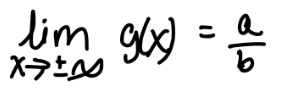
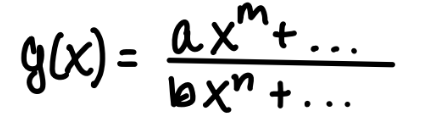
if m > n

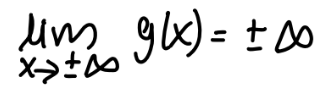
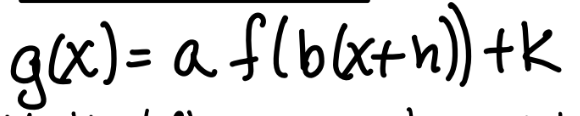
vertical stretch if

|a| > 1

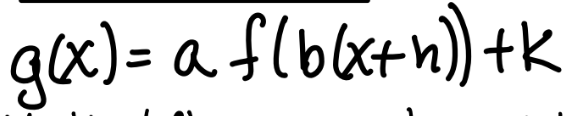
vertical compression if

|a| < 1

reflection over x-axis if

a is negative

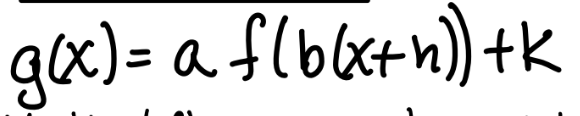
horizontal stretch if

|b| < 1

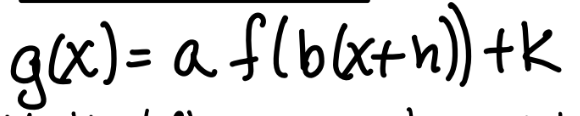
horizontal compression if

|b| > 1

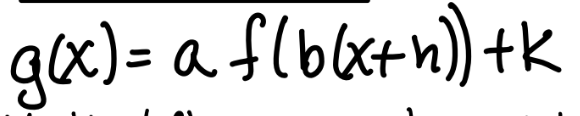
reflection over y-axis if

b is negative

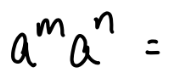
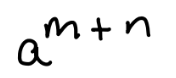
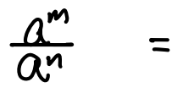
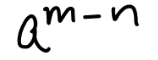
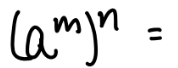
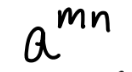
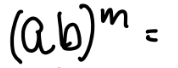
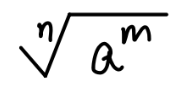
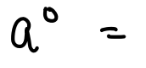
1

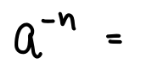
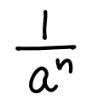
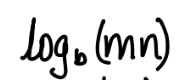
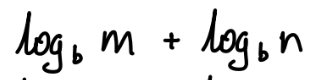
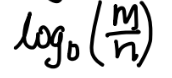
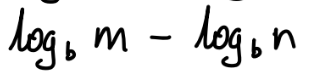
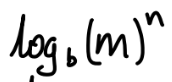
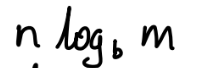
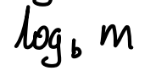
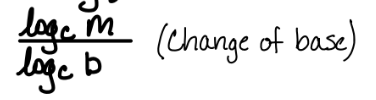
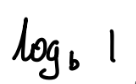
0

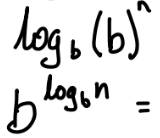
n

arithmetic sequence formula

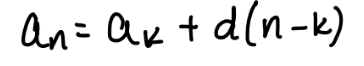
geometric sequence formula

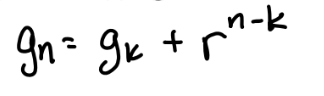
inverse functions numerically

f(a) = b then f^-1(b) = a

inverse functions graphically

inverse of f(x) is f(x) reflected over the line y = x

how to solve for inverse function algebraically

switch y and x and solve

inverse function verbally

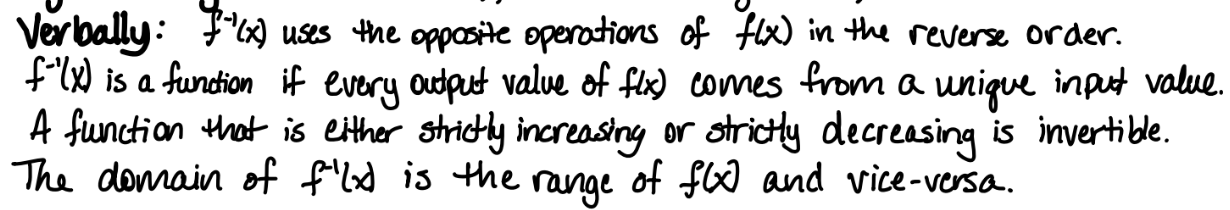
sin(x)

y/r

cos(x)

x/r

tan(x)

y/x

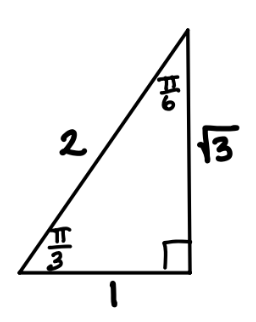
30-60-90 triangle

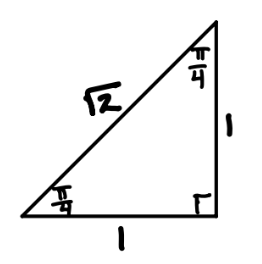
45-45-90 triangle

domain of arcsin

[-1,1]

range of arcsin

[-pi/2, pi/2] quadrants 1 and 4

domain of arccos

[-1,1]

range of arccos

[0, pi] quadrants 2 and 3

domain of arctan

[-∞, ∞]

range of arctan

[-pi/2, pi/2] quadrants 1 and 4

AROC on interval [a, b] with points (a, f(a)) and (b, f(b))

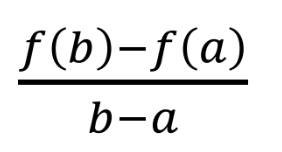
secant line

line formed between points a and b using the AROC formula

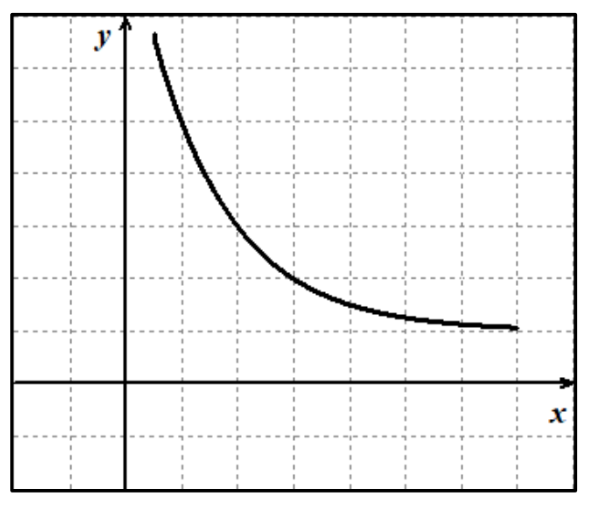
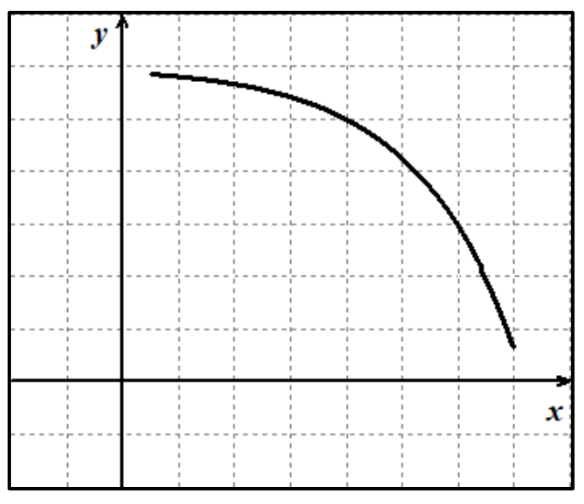
f(x) ___, ROC is ___, curve is ___

decreases, increasing, concave up

f(x) ___, ROC is ___, curve is ___

increases, increasing, concave up

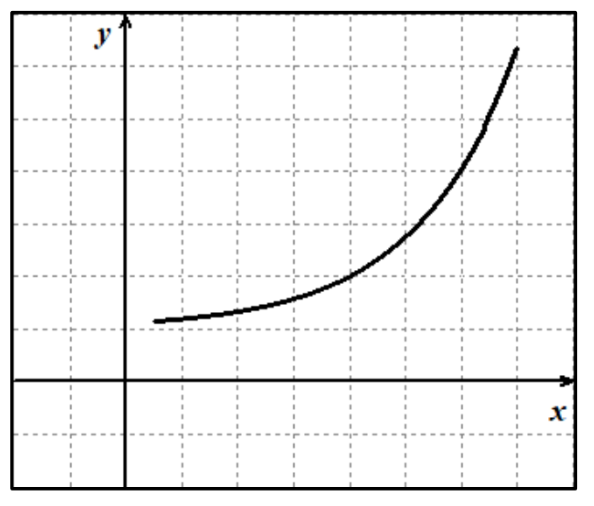
f(x) ___, ROC is ___, curve is ___

decreases, decreasing, concave down

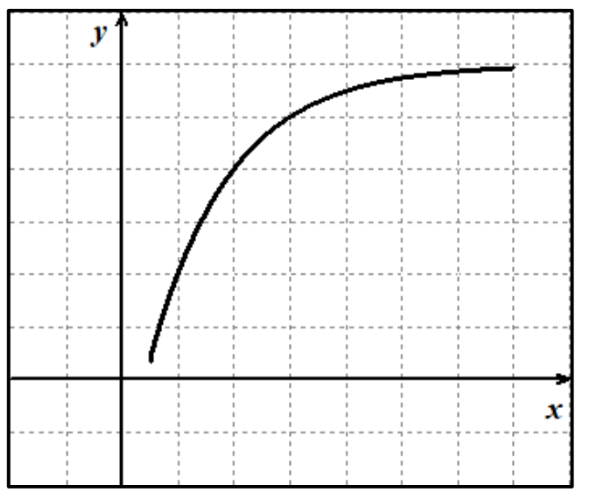
f(x) ___, ROC is ___, curve is ___

increases, idecreasing, concave down

if a polynomial function is increasing…

ROC is positive

if a polynomial function is decreasing…

ROC is negative

if a polynomial function is concave up…

ROC is increasing

if a polynomial function is concave down…

ROC is decreasing

point of inflection

ROC changes from increasing to decreasing or vice versa (CHANGE IN CONCAVITY)

odd function

f(-x) = -f(x) passes through origin

**if you can flip it upside down and it looks the same, it’s likely odd**

even function

f(-x) = f(x)

(x-a)¹

crosses x-axis (linearly)

(x-a)²

bounces (quadratically)

(x-a)³

bends (cubically)

if (a + bi) is a factor…

(a - bi) is a factor

end behavior of odd degree functions

opposites

end behavior of even degree functions

same

positive leading coefficient

up on right

negative leading coefficient

down on right

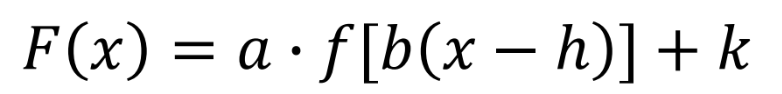
a value

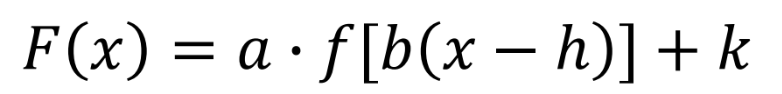
b value

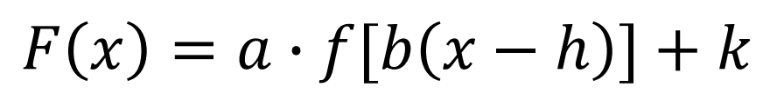
h value

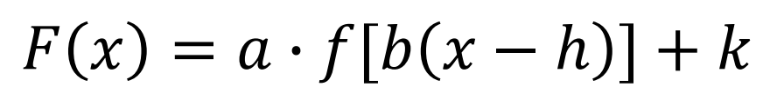
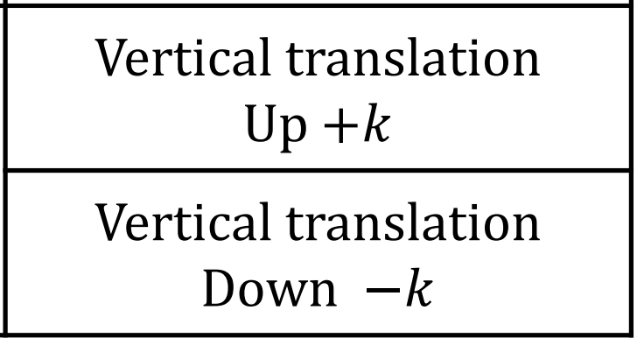
k value

linear function

If both input and output values change consistently

quadratic function

If input changes consistently and the 2nd differences of output values are equal.

cubic function

If input changes consistently and the 3rd differences of output values are equal.

exponential function

If input changes consistently and output values change proportionately

logarithmic function

If input values change proportionately and output values change consistently

is sin(x) odd or even?

odd

is cos(x) odd or even?

even

is tan(x) odd or even?

odd

how to calculate period of function

2∏/b for sin and cos

∏/b for tan

polar to rectangular formulas

x = rcosθ and y = rsinθ

rectangular to polar formulas

x² + y² = r² and tanθ = y/x

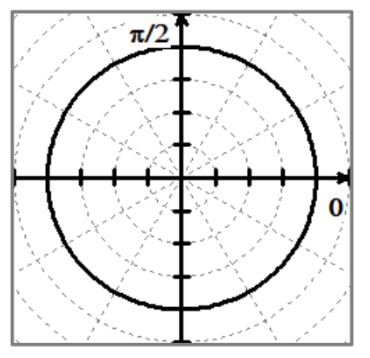
r = acosθ

r = a

r = asinθ

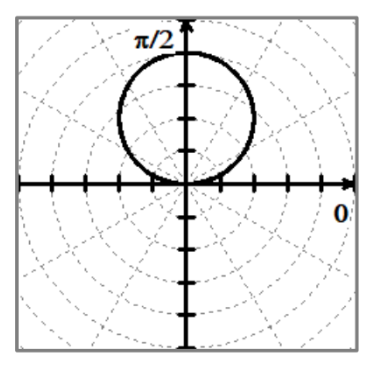
domain of circles

[0, 2∏]

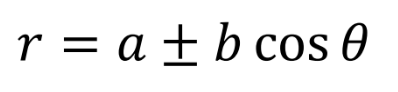
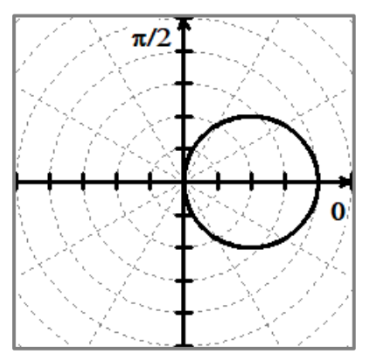
a/b = 1

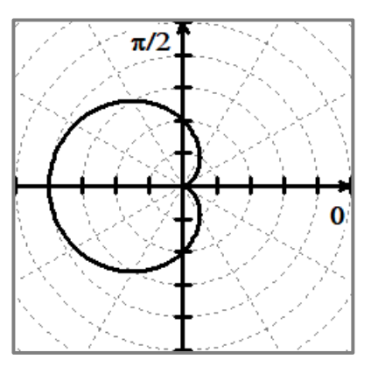
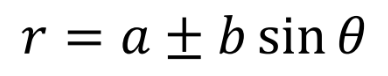
a/b = 1

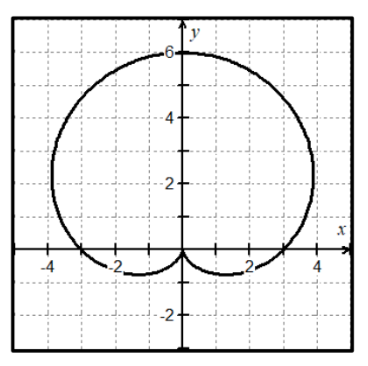
domain of cardioid

[0, 2∏]