STAT 3400 - Regression

Exam 1

RMSE

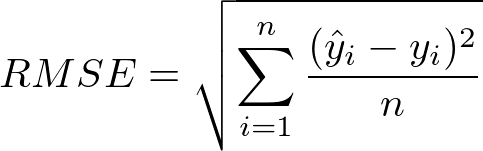
Flexible Model

adapts to changes better, non-parametric, needs more data, variance

Inflexible Model

less adaptable, parametric, needs less data, bias

Bias

error from approximating a real world system with a model, worse in inflexible models

Variance

error from fitting the model using training data that only represents a small subset of the population, too much leads to overfitting, worse in flexible models

CER

(sum of I(yi =/= yi_hat)) / n

RSS

E^T(E) = (y-XB)^T(y-XB), least squares seeks to minimize RSS, total squared error of the training model

Minimized RSS

B_hat = (X^TX)^-1(X^Ty)

RSE

sqrt(RSS/(n-2)), measure of how much the training data differs from the line of best fit

Overfitting

RSE is small but RMSE is bad, model too specific to training data to be useful

Multiple R²

1-RSS/TSS, the proportion of variance explained by the model, single linear regression

Adjusted R²

1-(RSS/TSS)((n-1)/(n-1-p)), the proportion of variance explained by the model, multiple linear regression

TSS

sum of (yi - y_bar)², sum of the squared differences between the training data and the mean (null)

MSE

RSE² = RSS/(n-1-p), estimate of the variance of the model

MSG

(TSS - RSS)/p, compares the performance of the null and fitted models, larger MSG values indicate that the model outperforms the null

F

MSG/MSE, used in ANOVA tests, values near 1 indicate the model does not improve the null, values greater than 1 indicate that it did, if the ratio is big, the model is more accurate, the larger the ratio the more likely one of the predictors is useful.

Explain one of the uses of an unsupervised statistical learning model.

To find the association between predictor variables. For example, cluster analysis groups data into groups to determine association. (add some more stuff for the exam)

Multiple linear regression with 5 predictors, test set of 250 observations. If yi is the actual response for the i-th observation and yi-hat is the predicted response, which equation models RMSE

• sqrt ( sum from 1 to 250 of (yi–yi-hat)^2/250 )

Model to predict fish weight with RMSE of 0.75 lbs. In order to determine benefit we should compare 0.75 lbs to the error obtained from the model that always predicts _____.

• The mean fish weight (null model)

Explain the benefit of using RMSE rather than MAE (mean absolute error)

• Both have the correct units. Squared error penalizes really big errors more than absolute error, and really tries to avoid models with massive errors. RMSE doesn’t have the kink where MAE isn’t differentiable.

Which of the following is NOT a component of testing error? Bias error, variance error, flexibility error, irreducible error.

• Flexibility error (does not exist)

Tow numerical variables and observe a strong, increasing, nonlinear relationship. If we train a simple linear regression model we can expect the ______ component of testing error to be relatively large. Bias or variance.

• Bias

Two variables with a strong, decreasing, linear relationship. Train and test a 5th-order polynomial function and discover we have overfit the data. The ___ error was small but the ____ error was large.

• Training, testing

Explain the bias-variance trade-off inherent in the flexibility of a statistical model.

• Three types of error: bias, variance, and irreducible. If a model is too inflexible there will be more bias. If a model is too flexible there will be more variance. If bias decreases, variance increases. One has to try to balance the two types of error.

Training set of 1000 emails and a testing set of 100. Binary response spam/not spam. 600 labeled as spam in training, 55 labeled as spam in testing. What is the upper bound on the CER against a testing set for any new model to be useful? 40% 45% 55% 60%

• 45% - null model accuracy

After training a multiple logistic model with 6 predictors we want to assess accuracy against a test set of 125 observations. Which is CER

• Sum from 1 to 125 ( I(yi =/= yi-hat) /125 )

After estimating a simple logistic model you obtain a logarithmic function. For a given input the output of the function is ____.

• P(y=1)

Explain how to commit CER of the given dataset

• Decide on a threshold of success/failure, convert probabilities (p-hats) to y-hat values, compare to the true y response, determine what proportion of the time the model is wrong, and take the mean.

A linear regression model is considered simple if it has only one ______.

• Predictor

Suppose yi is the true response and yi-hat is the predicted based on the model B0+ B1xi. Assuming there are n observations, the least squares algorithm seeks to minimize which quantity (what is RSS)?

• Sum from i=1 to n ( (yi - yi-hat)^2 )

Estimate a simple linear regression. Training set with 250 observations and you do least squares method using the matrix notation below. What are the dimensions of B-hat?

• 2 rows by 1 column (B0 and B1 column vector)

Describe the shape, direction, and strength of association between these two variables

• Linear, negative/decreasing, strong/moderate

Fit a linear regression and test the hypothesis H0: B1=0, HA: B1=/=0 based on a significance level of alpha = 0.1, What is the interpretation of alpha?

• We accept a 10% chance of finding an association between the predictor and response when in fact there is none

Inferential analysis of a simple linear regression mode we might constrict the confidence interval below B1 +- z_a/2 * SE_B1. In the formula z_a/2 represents the number of standard errors on the ______ distribution.

• Standard normal

Null distribution with a test statistic inside the 0.05 significance level bounds. What is the appropriate conclusion?

• No evidence to suggest that B1 =/= 0, fails to reject the null distribution, not beyond the rejection threshold

Given a sampling distribution for birth weight (x) and father’s age (y) with a 95% confidence interval

• 95% confident that the true slope parameter is between [] and []. 95% confident that for every one-year increase in a father's age, the baby’s birth rate will increase by between [] and []. Say something about zero being in the interval, possible that there is no relationship.

Summary output with RSS 11.79. What does RSS mean

• On average, the margins of victory in the training data differ from the model by about 11.79 points

The RSS measures error when using the fitted linear regression mode. The TSS measures the error when using the ______.

• Mean response value (the null)

Explain how R^2 is related to the variance in the response variable

• R^2 is the proportion of variance eliminated/explained in the fitted model as compared to the null model

Using 300 observations to train an MLR model to predict penguin body weight using 3 predictors. What are the values of n and p?

• n=300, p=3

What formula would compute RSS? Given RSE is 11.79 and there are 999 observations and 4 predictors

• RSE = sqrt(RSS/n-(1+p)), so RSS = 11.79^2*995

Which of the following is false regarding adjusted (multiple) R^2?

R^2 represents the proportion of variability in the response explained by its relationship with the predictors.

R^2 cannot be less than adjusted R^2.

R^2 will always decrease when we add predictors to the model.

• R^2 will always decrease when we add predictors to the model - always increases

Estimate two different LR models using a training set with 400 observations. First has 3 predictors, second has 14. Given Adjusted R^2 = 1 - (RSS/TSS)((n-1)/(n-1-p))

• TSS and number of observations are the same. p and RSS will be different.

Conduct an ANOVA with 3 predictor variables. One type of variance is MSG, the formula of which is (TSS-RSS)/p. The TSS measures the error in a model that employs ______ predictor variables

• 0 (null model)

Using ANOVA, get the graph. F-statistic for the test statistic is to the left of the F-distribution for the null distribution (threshold). Meaning

• Not rejecting the null, so none of the predictor variables are associated with the response

To explain the margin of victory perform ANOVA. What are the hypotheses associated?

•  H_0: B1=B2=B3=0, H_A: at least one Bj=/=0

Explain the test statistic on the F distribution (F= MSG/MSE)

• MSE is the amount of error in the fitted model (want it to be small). MSG is how much error is in the model relative to the null (want it to be big). If the ratio is big, the model is more accurate. The larger the ratio the more likely one of the predictors is useful.