Rotational dynamics & Newtons 2nd law for rotational motion

centripetal force

• provides the centripetal acceleration

  • Fc = mv² / r 

• makes the object turn

• w/o it the object would move in a straight line (diff between linear and rotational motion) 

Fc = mv² / r

what is the equation for centripetal force (Fc)? 

makes the object turn

what effect does the centripetal force have on an object?

tangential force

• provides a tangential acceleration and an angular acceleration

  • Ft = mαt = mrα 

• makes the object speed up or slow down

• changes how FAST the object turns (so its related to the angular acceleration) 

Ft = mat = mrα

what is the equation for tangential force (Ft)? 

makes the object speed up or slow down

what effect does the tangential force have on an object?

the magnitude of the torque produced by the tangential force

• t = rFt = r(mrα) = mr²α

t = rFt = r(mrα) = mr²α

what is the equation for the magnitude of the torque produced by the tangential force?

I = mr² 

what is the moment of inertia (I) of the particle? 

Newton’s 2nd law applied to rotational dynamics

• T = Iα

• torque = moment of inertia × the angular acceleration

force = torque, mass = moment of inertia, acceleration = angular acceleration

remember: force = torque, mass = moment of inertia, acceleration = angular acceleration

Tnet = Iα

Fnet = ma →?

ω is rotational velocity or how fast something is spinning, if question asks how fast something is moving you need to convert ω→v

remember: ω is rotational velocity or how fast something is spinning, if question asks how fast something is moving you need to convert ω→v

Vf = r(ωf)

what is the equation to convert ω→v (rotational to linear velocity)?

if we model the pulley as being massless, we are basically replacing it with a peg and ignoring it. In this case, the tension in the rope is the same on each side of the pulley

remember: if we model the pulley as being massless, we are basically replacing it with a peg and ignoring it. In this case, the tension in the rope is the same on each side of the pulley

when we dont ignore the mass of the pulley, then the tensions in the strings on either side of it are not equal (otherwise there would be no net torque on the pulley and it would be in equilibrium) (realistic)

remember: when we dont ignore the mass of the pulley, then the tensions in the strings on either side of it are not equal (otherwise there would be no net torque on the pulley and it would be in equilibrium) (realistic)

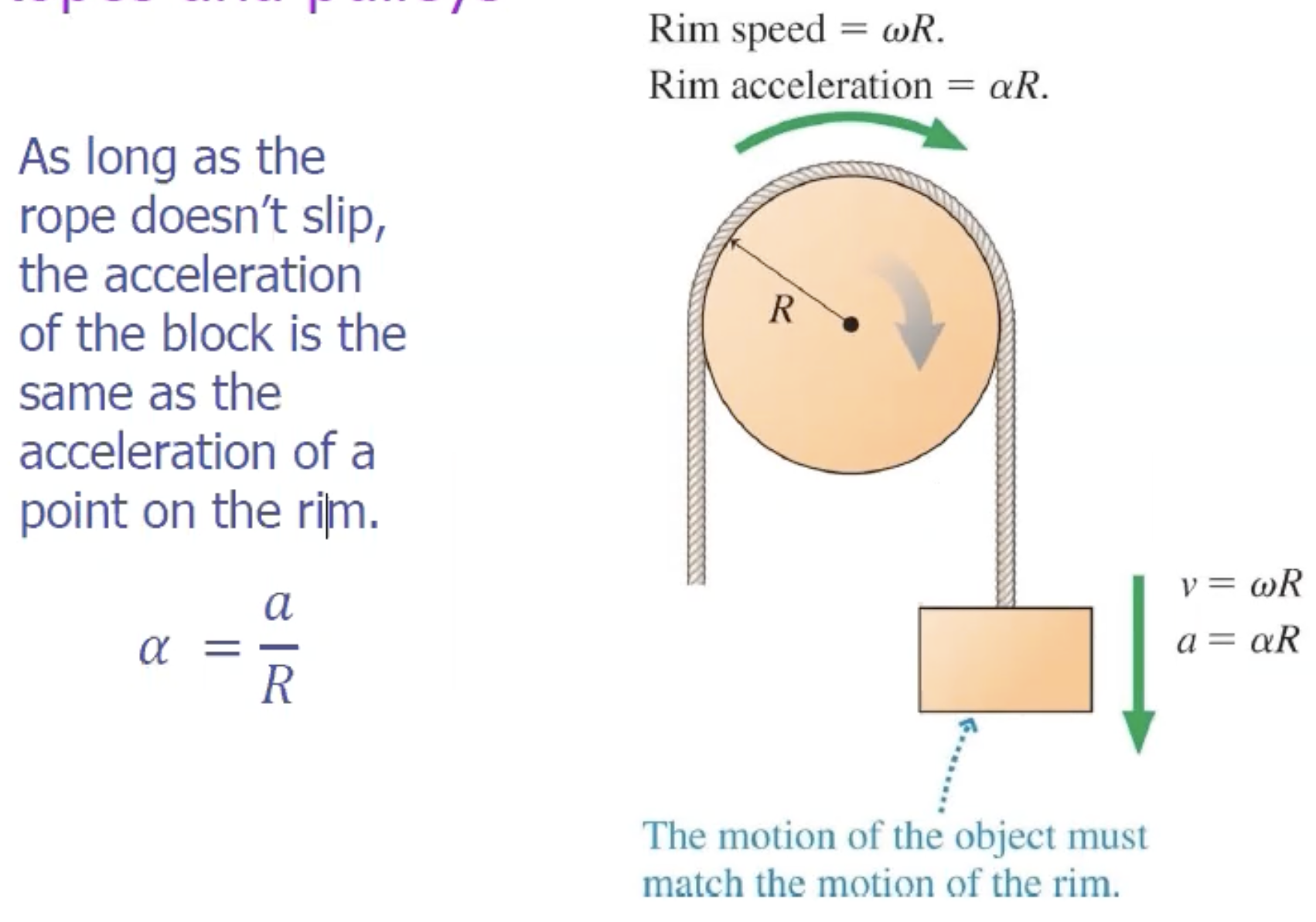
as long as the rope doesnt slip, the acceleration of the block attached to the rope is the same as the acceleration of a point on the rim

remember: as long as the rope doesnt slip, the acceleration of the block attached to the rope is the same as the acceleration of a point on the rim

α = a / R

• rim speed = ωr

• rim accel = αω

• v = ωr 

• a = αω

• α = a / R