econ 373

game theory !

players

who’s involved

strategy

choices available to the players

what they can do

complete set of instructions for playing the game

strategy set

all the options they can choose from

straegy combination

a set of strategies for all players which fully specifies all actions in a game

must include 1 and only 1 strategy for every player

preference ordering

what would they prefer

payoff function

describes the outcome of a game for a player

strategic forms

simultaneous games

features a payoff matrix

extensive form

sequential games
features a game tree

decision node

a player’s choice of movement that they could choose

seen in extensive form games

terminal node

happens at the end of game

says the payoff of that path

kiss

keep it simple stupid

best response

best strategy to each move the opponent makes

non-cooperative games

games in which player choose their strategies independently

unique best response

mutually consistent best response

nash equilibrium

a strategy combination in which everybody is playing their best response

strict nash equilibrium

a strategy combination in which everybody is playing their unique best response

strongly dominant strategy

UBR to all possible SC of all players

weakly dominant strategy

BR to all SC, UBR to at least 1

strong dominant strategy equilibrium

everyone’s strongly dominant strategy matches with the others

weak dominant strategy equilibrium

at least 1 strategy is weakly dominant

rational players

individuals pursue their own self-interest , choose what they most prefer

common knowledge

pareto-optimal

no other feasible or attainable situation such that at least 1 person is better off and no-one is worse off

pareto-dominates

at least 1 person is better off w/ strategy A than w/ B
no-one is worse off with strategy A than with B

pareto-frontier

the set of all pareto-optimal strategy combinations

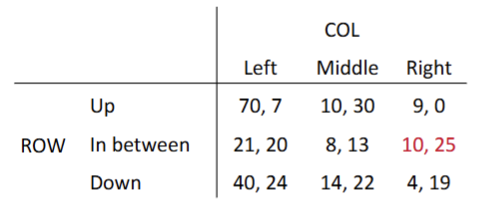
which combinations are in the pareto frontier

{(up, left), (up, middle), (down, left)}

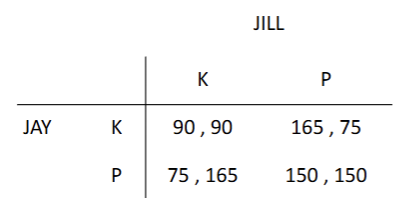
which is the NE? is it dominant? is it strict? is it pareto-optimal? which are the pareto-optimal strategy combinations

(k,k)
strict dominant strategy

not pareto-optimal
everything except the NE is pareto optimal

certainty equivalent (ce)

the price between the riskless prospect and the risky prospect in which your indifferent between

(1: ___)

expected value (ev)

probability weighted average of winnings from the prospect

notation for risky prospects

(p₁, p₂, …. p_n : w₁, w₂, …. , w_n)

risky prospects

price w1 with probability 1 and so on and so forth
probabilities must equal 1

expected value of prospect (1:w_i)

ev((1 : w_i)) = 1 x w_i = w_i

ev((p1, p1,….,pn : w1, w2, …. , wn)) = p1w1 + p2w2 + … + pnwn

bernoulli payoff function

U(w)
U = sqrt(w)
function U(w) is supposed to capture the preferences of the person who is doing the choosing

expected utility (eu)

the probability weighted average of the utility of winnings from the prospect
__((p1,p2, …, pn : w1, w2, …., wn)) = p1U(w1) + p2U(w2) + … + pnU(wn)
(the sum of pnU(wn) added together)

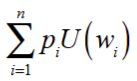
expected utility hypothesis

for every person there exists a payoff function, U(w), such that

• the person prefers prospect A to prospect B if and only if the expected utility of prospect A is larger than the expected utility of prospect B

• the person is indifferent between prospects A and B if and only if the expected utility of prospect A is equal to the expected utility of prospect B

non-satiation assumption

larger prizes are preferred to smaller prizes

risk of a prospect

the volatility or variation in the returns from it

the higher the volatility → the larger the risk

how to measure risk

the variance of the returns offered by the prospect

variance of returns

the sum
__ ((p1, p2, …, pn : w1, w2,…., wn)) = p1 (w1-ev)² + p2(w2 - ev)² + … + pn(wn - ev)²

positive var

any prospect in which all of the probabilities p_i are strictly less than 1

indicative of risk

risk averse

for a risky prospect
ce < ev
concave graph

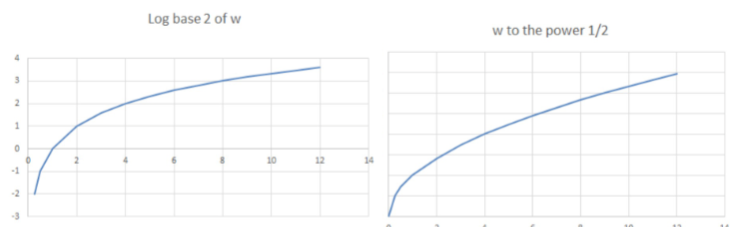
risk inclined

for a risky prospect
ce > ev

convex graph

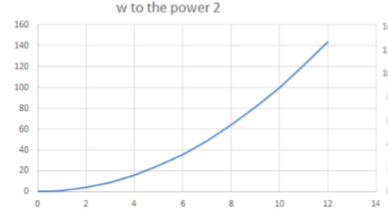
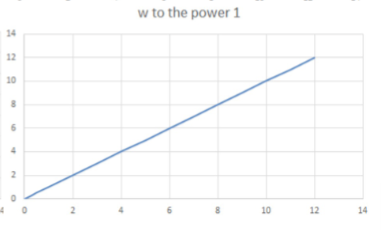
risk neutral

for a risky prospect
ce = ev
linear graph

expected utility theorem

person prefers prospect A to prospect B if and only if the EU of prospect A is larger than than the EU of prospect B

continuity axiom

prospect → w1, wk, wn → 1 < k < n

there exists a probability e_k in the open interval (0, 1) such that the person about whom we are talking is indifferent between (0,1,0 : w1, wk, wn) and (1- e_k, 0, e_k : w1, wk, wn)

decision makers are indifferent between a gamble and a specific probabilistic combination of a more preferred and a less preferred gamble

mixed strategy

a just probability distribution over the player’s pure strategies or actions

mixed strategy set

the set of the probability distributions over the player’s pure strategies or actions

evolutionary game theory

seeks to identify patterns of behaviour in populations that are evolutionary stable

evolutionarily stable strategies

a strategy that, when adopted by most of a population, cannot be invaded or replaced by alternative strategies

monomorphic population

whole population consists of 1 type

fitness

the likelihood of reproductive success in a species

polymorphic population

neither pure phenotype can be an evolutionary stable strategyq

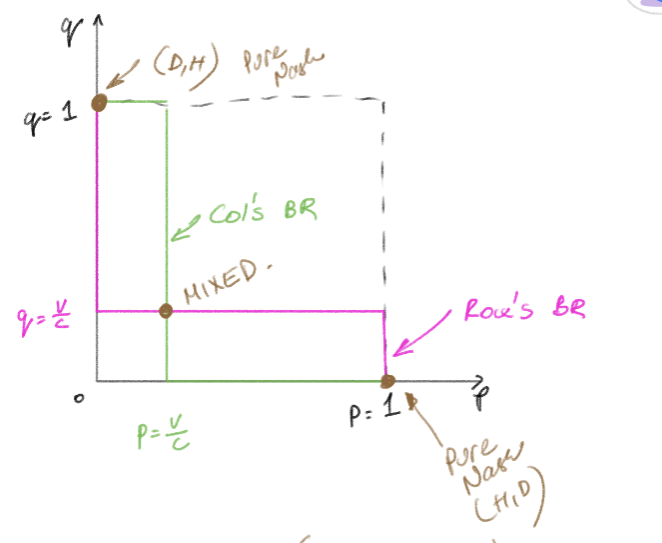
strategy sapce

a graph that shows every possible strategy that can be played along with the chances in which they would be played

length of a subgame

the number of decision nodes along the longest path contained in the subgame

subgame

smaller game within a larger game

path

a sequence of moves and their subsequent outcomes, starting from the initial node and culminating in a terminal node

strategy combinations in extensive forms

composed of a strategy for both players

must specify an action for each decision node (/player)

subgame perfect equilibrium

for every subgame, the strategy combination induced by the SPE strategy combination is a NE strategy combination for that game

kuhn’s algorithm - backward induction

beginning with the subgames (or subgame) of length 1

• find the choices or actions that maximize the payoff of the players who are called upon to make choices at these nodes

prune the game tree by xing out the branches that correspond to actions that are not equilibrium actions in the subgame under consideration

• continue working backwards until you’ve found the equilibrium action (or actions) for the longest subgame (or subgames), you have found the SPE strategies of all players

credible promises

“I (person B) promise that if you (person A) choose w instead of x, I will choose y instead of z”

if action w (having been taken by person A), person B is better off keeping her promise (by taking action y) than she would be if she did not keep it (by taking action z)

credible threats

“if you (person A) chooses x instead of w, I (person B) will choose y instead of z”

if action x (having been taken by person A), person B is better off fulfilling her threat (by taking action y) than she would be if she did not fulfill it (by taking action z)

ordinal payoffs

ranking all the outcomes from best to worst (based on highest number to lowest)