Directional Fields, Euler's Methods, Applications of Diff Eqns

for every differential eqn, there is a

infinite amount of “solns” to the differential eqn

• therefore, there is generally a FAMILY of solns that have a general form

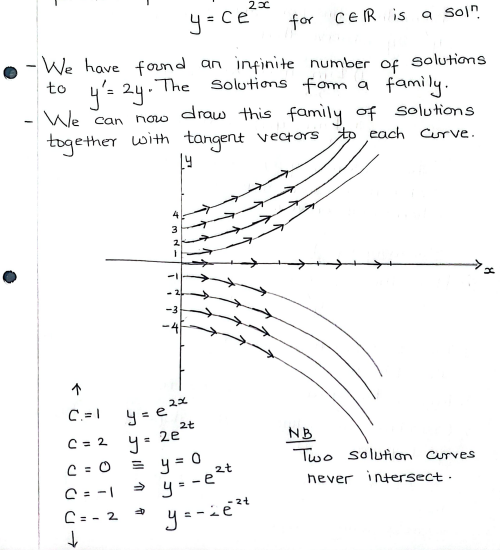
• ex: f’(x) = 2*f(x) or y’ = 2y, the soln can be any soln of the form y = ce^(2x) for every c that’s a real num

directional field for the differential eqn y’ = 2*y (example)

• two solns of a diff eqn NEVER INTERSECT

• observe that the lim of y(x) as x → infy = infy IF y(0) > 0 (all the solns above the x-axis)

• and the lim of y(x) as x → infy = -infy IF y(0) < 0 (all the solns below the x-axis)

• each soln has their own unique initial condition of y(0)

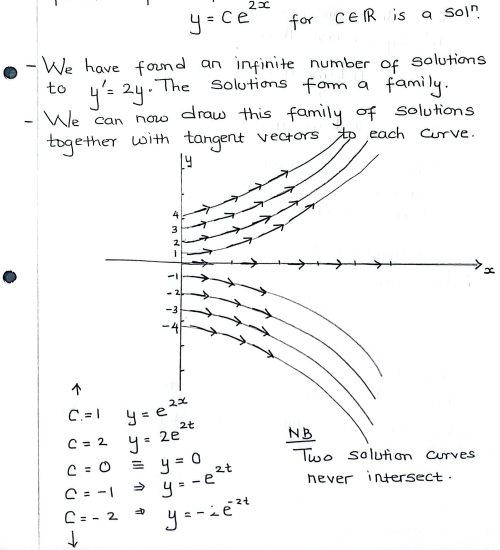
directional field

a graph of some solutions of the given diff eqn

• using arrows, draw the soln curves that start from their own unique initial condition y(0) (x = 0, y(0))

equilibrium soln

in the example in the image (y’ = 2y), the soln y(x) = 0 because the fn is a constant value (yields a horizontal line)

procedure of drawing a directional field

euler’s method concept

• a numerical method for finding explicit/implicit solns that works for almost all diff eqns

• uses the tangent at certain pts and you keep shifting the x-val until you find the estimated path of the soln/you can approximate the output value from the soln fn at some given x-pt

formulas for euler’s method

x0 = “prev” x-val or start x-val

y0 = “prev” y-val or start y-val

x1 = “next/current” x-val

y1 = “next/current” y-val

h = the “small step”, constant val, usually given to you, the amount the x-val is “shifted” each step

f(x0, y0) = the tangent/slope at the “prev” coord (x0, y0)

**f(x,y) = dy/dx

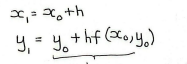
method for euler’s method

• the goal is that when you are given a diff eqn (y’), you must approximate y(x) for some given x pt

exponential growth basics

• a fn that maps out how quantities grow or decay at a rate proportional to their size

• a quantity y that grows/decays at a rate proportional to its size fits w the eqn of the form:

• dy/dx = ky (the RATE = constant * quantity, where quantity abides by its own growth/decay eqn)

exponential growth: dy/dx = ky, if k < 0:

• eqn is called the LAW OF NATURAL DECAY

exponential growth: dy/dx = ky, if k > 0:

• the eqn is called the LAW OF NATURAL GROWTH

exponential growth: dy/dx = ky, general form of the solution:

y = ce^(kx) for some c that’s a real num

exponential growth: population growth eqn model

dP/dt = kP and P(t) = P(0)*e^(kt) where P(0) is some initial population at some initial time

exponential growth: radioactive decay model

m(t) = m(0)*e^(k*t)

• m(t) = mass of the substance at time t

• m(0) = mass at t = 0

• k = rate of decay

half life of a substance

the amount of time required for HALF of the mass of the quantity to decay

newton’s cooling law

rate of cooking of an obj is proportional to the temp diff between the OBJ and its SURROUNDINGS provided the temperature diff isn’t super significant

newton’s cooling law: formulas

dT/dt = k(T - Ts)

dT/dt = ky for y = T - Ts

• T = temp of object

• Ts = temp of surroundings

• t = time

• k = rate of cooling

newton’s cooling law: formulas cont’d

T(t) = temp of the obj after t minutes

y = T - Ts

y(0) = T(0) - Ts (Ts is a constant val)

and y(t) = y(0)*e^(kt) = k(T(0) - Ts)

y(t) = T(t) - Ts

continuously compounded interest: formulas

A = A(0)*(1 + r/n)^(nt)

A(0) = initial amount of money invested

r = interest rate

t = number of years

n = the amount of times the interest rate is compounded per year

continuously compounded interest: formulas 2

A = A(0)*(1 + r/n)^(nt)

r/n = in each compounding period, the rate is r/n

nt = compounding periods in t years

continuously compounded interest: formulas 3 (the most important)

A(t) = A(0)*e^(rt)

therefore, dA/dt = rA(0)e^(rt) = r*A(t) (which is the above line)