IN1150 - Logiske Metoder - Begreper

Begreper for Logiske metoder

Utsagn

Noe som kan være sant eller usant

Atomære

Kan ikke deles mer

Sammensatte utsagn

atomære utsagn satt sammen ved hjelp av bindeord

Utsagnsvariabel

en variabel som representerer en atomær formel

Logiske konnektiver

∧,∨,→,¬

Negasjon

¬ F, “ikke F”

Konjunksjon

F∧G, “F og G”

Disjunksjon

F∨G, “F eller G”

Implikasjon

F → G, “Hvis F, så G”

Hovedkonnektiv

Det ytterste konnektivet, det konnektivet som blir regnet sist i et sammensatt utrykk

Tilstrekkelig

P er tilstrekkelig for Q betyr at hvis P er sant, så må Q være sant. Tilsvarer P → Q. Q trenger ikke være usant når P er isant, men den må være sant når P er sant.

Nødvendig

P er nødvendig for Q betyr at P må være sant for at Q skal være sant. Hvis P er usant er det garantert at Q er usant. Tilsvarer ¬P → ¬Q eller Q→P

A↔B

A hvis og bare hvis B

Presedensen

Hvem binder sterkest, typ regnerekkefølge; nkdi, noen kan det ikke, ¬∧∨→. ∀ og ∃ binder like sterkt som ¬

Valuasjon

Tilordning av sannhetsverdier, skrives med v

Sannhetsverditabell

En tabell som viser sannhetsverdien til en sammensatt utsagnslogisk formel på bakgrunn av hvilke sannhetsverdier som er tilordnet utsagnsvariablene

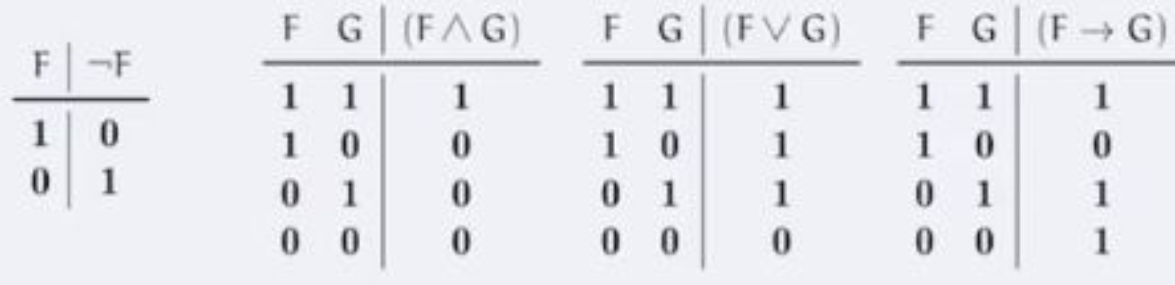
Logisk ekvivalens

To formler F og G er ekvivalente dersom de har samme sannhetsverdi for enhver tilordning av sannhetsverdier. Dvs. at F er alltid sann når G er sant og vice versa. F ⇔ G

Distributive lover

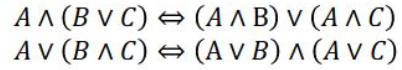
De Morgans lover

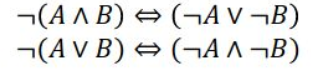
Assosiative lover

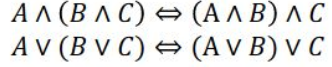
Kommutative lover

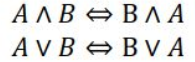
Dobbel negasjon

¬¬A ⇔ A

Implikasjon

A → B ⇔ ¬A ∨ B

Logisk ekvivalens

M er en mengde av utsagnslogiske formler. F er en utsagnslogisk formel. Hvis F er sann for alle valuasjoner som gjør alle formlene i M sanne samtidig, er F en logisk konsekvens av formlene i M, og vi skriver dett som M ⊨ F

Gyldig/holdbart argument

Hvis konklusjonen er en logisk konsekvens av premisser

Oppfyllbarhet

v gjør F sant, i dette tilfelle skriver vi v ⊨ F. Vi sier at F er oppfyllbar dersom det finnes det finnes en valuasjon som oppfyller F

Falsifiserbarhet

v gjør F usant. Vi sier at F er falsifiserbar dersom det finnes en valuasjon som falsifiserer den.

Tautologi/gyldighet

Hvis F er sant for alle valuasjoner, ⊨F

Motsigelse/kontradiksjon

Hvis F er usant for alle valuasjoner

⊤

Utsagnslogiskformel som heter “topp” eller “sann”

⊥

Utsagnslogiskformel som heter “bunn” eller “usann”

Uavhengig formel

En formel F er uavhengig av en mengde formler M hvis hverken F eller ¬F er en logisk konsekvens av M

Uavhengig mengde

En mengde formler er uavhengig hvis enhver formel er uavhengig av mengden av de andre formlene

Bevis

En rekke logiske slutninger som viser hvordan vi kommer fra antakelse til påstanden

For hvert steg må konklusjonen være en logisk konsekvens av antakelsene

Formodning

En påstand som vi tror, eller har god grunn til å tro er sann, men som vi ikke har bevist eller motbevist

Direkte bevis

Vi har en påstand på formen “hvis F, så G”. Et direkte bevis bevis begynner med antakelsen om F er sann og ender med konklusjonen om at G er sann

Eksistansbevis

Vi har en påstand som sier at noe eksisterer. Finn et objekt som gjør påstanden sann. Gi en metode for å finne et slikt objekt.

Bevis ved tilfeller

En bevismetode hvor hvert enkelt tilfelle blir bevist hver for seg

Bevis for universelle påstander

En påstand som sier noe om alle objekter av en bestemt type. For å bevise påstanden, begynn med å velge et vilkårlig objekt fra den gitte mengden og vis at dette objektet har den ønskede egenskapen.

Moteksempler

Den letteste måten å motbevise en unviersell påstand er å komme med et moteksempel

Kontrapositive bevis

Påstanden er “hvis F, så G”, men den er logisk ekvivalent med ¬G → ¬F. Kontrapositiv bevis bruker denne ekvivalensen for å bevise en påstand

Motsigelsesbevis

Begynner med å anta at påstanden er usann og viser hvordan denne antagelsen fører til en motsigelse

Konstruktiv bevis

Viser fram eller gir en metode for å finne et objekt

Ikke-konstruktiv bevis

Viser ikke objektet eller gir en metode

Binære relasjon fra S til T

En delmengde av S X T (kartesisk produkt)

Binære relasjon på mengden S

En delmengde av S X S

n-ær relasjon

En delmengde av A1 x … x An

n-ær relasjon på mengden A

En delmengde av A x … x A

Identitetsrelasjonen

{<x,x>| x ∈ S}

Den tomme relasjonen

Ø

Den unvierselle relasjonen

mengden S x T

Infiksnotasjon

anta at <a,b> ∈ R, da kan vi skrive dette sånn aRb

refleksiv

Relasjonen R er refleksiv dersom det for alle x i S er slik at <x,x> ∈ R

symmetrisk

Relasjonen R er symmetrisk hvis det for alle x, y er slik av hvis <x,y> ∈ R så er <y,x> ∈ R

transitiv

Relasjonen R er transitiv hvis det for alle x, y, z er slik at hvis <x, y> ∈ R og <y, z> ∈ R så er <x, z> ∈ R

Ekvivalensrelasjon

Er en relasjon som er refleksiv, symmetrisk og transitiv

anti-symmetrisk

En relasjon R er anti-symmetrisk hvis det for alle x, y er slik at hvis <x, y> ∈ R og <y, x> ∈ R så er x = y

irrefleksiv

Relasjon R er irrefleksiv hvis det ikke er noen x ∈ S slik at <x, x> ∈ R

Partiell ordning

En relasjon som er refleksiv, transitiv og anti-symmetrisk

Total ordning

En partiell ordning kalles en total ordning hvis det hvis det for alle x og y i S er slik at xRy eller yRx

asymmetrisk

Relasjonen R er asymmetrisk dersom det er slik at hvis xRy så er ikke yRx

f: A → B

f er funksjonen fra A til B. A: definisjonsområdet og B: verdiområdet

Identitetsfunksjonen

idA(x) = x, funksjonen der verdien er lik argumentet

injektiv/en-til-en

Funksjonen f er injektiv/en-til-en dersom det for alle x,y ∈ A slik at x ≠ y så er f(x) ≠ f(y)

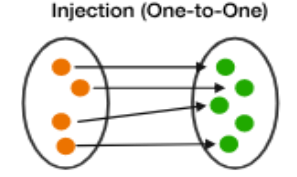
surjektiv/på

Funksjonen f er surjektiv/på dersom det for alle y ∈ B, finnes en x ∈ A slik at f(x) = y

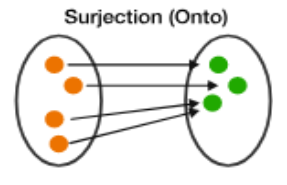
bijektiv/en-til-en korrespondanse

Funksjonen f er bijektiv/en-til-en korrespondanse, dersom den er både inektiv og surjektiv

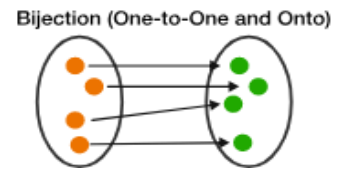
Bildet av

La X være en delmengde av A. Da kalles {f(x)|x∈X} bildet av x under f, og skrives f[X]

Bildemengden

Bildet av hele A under f, altså f[A]

Unær operasjon

En unær operasjon på en mengde A er en funksjon fra A til Å

Binær operasjon

En binær operasjon på en mengde A er en funksjon fra A til A x A

Den universelle mengden

Alle kontekster har en undeliggende mengde som inneholder alle elementer

Komplementet

Komplementet til mengden M er mengden av alle elementer som er i den universelle mengden, men ikke i M. Komplementet til M skrives 𝑀‾.

Potensmengden

Potensmengden til en mengde M er mengden av alle delmengder av M.

Kardinalitet

Kardinalitet betyr intuitivt «størrelse». To mengder har lik kardinalitet hvis det finnes en bijeksjon mellom dem. Mindre kardinalitet betyr at det finnes en bijeksjon mellom en mengde og en delmengde av den andre. Hvis M er endelig, er kardinaliteten til M lik antall elementer i M

Tellbar

En uendelig mengde M er tellbar hvis det er en en-til-en korrespondanse mellom elementene i M og de naturlige tallene. Alle endelige mengder er tellbare.

Overtellbar

Hvis det ikke er en en-til-en korrespondanse mellom elementene i M og de naturlige tallene.

Mengde lukket

At M er lukket under en gitt operasjon på A betyr at når vi utfører denne operasjonen på ett eller flere elementer i M, så er vi garantert å få et element i M.

Tilukningen

Den minste mengden som inneholder M og er lukker under en eller flere operasjoner kalles tilukningen av M.

Tilukningen av R

Den minste mengden som inneholder R og har en gitt egenskap(eks. refleksiv, symmetrisk, transitiv) kalles tilukningen av R

Induktivt definert mengde

En induktiv definert mengde er den minste mengde som inneholder en gitt mengde (basismengde) og som er lukker under gitte operasjoner.

Å definere en mengde induktivt har tre steg:

1. Basissteget: å spesifisere basismengde

2. Induksjonsteget: Å spesifisere operasjonene

3. Tilukningen: å ta den minste mengden som inneholder basis mengde og er lukket under operasjonene

Konkatenering

Operasjonen som består av å slå sammen lister, strenger eller språk: To strenger s og t slås sammen til én, st. To lister, L og M, slås sammen med funksjonen + til L+M, for eksempel (1,2,3)+(4,5,6)=(1,2,3,4,5,6)(1,2,3)+(4,5,6)=(1,2,3,4,5,6). Hvis L og M er språk, er konkateneringen av L og M, språket LM={st∣s∈L og t∈M}.

Rekursivt definerte funksjoner

En rekursivt funksjon f med definisjonsområdet M defineres slik:

1. Basissteget: for hvert element x i basismengden, spesifiserer vi en verdi f(x)

2. Rekursjonssteget: for hvert element x i M som forekommer i induksjonsteget, definerer vi verdien f(x) ved å bruke de tidligere definerte verdiene for f

Matematisk induksjon

Bevismetode for å vise at en påstand er sant for alle natulige tall.

1. Basissteget: Vis at påstanden holder for tallet 0

2. Induksjonssteget: Hvis påstanden holder for et vilkårlig tall n (induksjonshypotesen), så holder den for n + 1

Strukturell induksjon

Bevismetode for å vise at noe er sant for alle elementer i en induktiv definert mengde.

1. Basissteget: Bevis at påstanden holder for alle elementer som kommer i basismengde

2. Induksjonssteget: Hvis mengden er lukker under en operasjon som gjør at x fremkommer fra x1, x2, …, xn og påstanden holder for alle disse (induksjonshypotesen), holder påstanden også for x

Førsteordens logikk

Utvider utsagnslogikk med blant annet kvantorer

Kvantorer

∀, leses som «for alle», ∃, leses som «det finnes»

Førsteordens språk

Består av følgende:

Logiske symboler:

• De logiske konnektivene ∧,∨,→ og ¬

• Kvantorene ∀ og ∃

• En uendelig tellbar mengde av variabler

• Parenteser og kommaer

Ikke-logiske symboler:

• Mengden av konstantssymboler

• Mengde av funksjonssymboler

• Mengde av relasjonssymboler

Aritet

Egenskap ved funksjons- og relasjonssymbol som forteller hvor mange termer som trengs for å lage henholdsvis termer og atomære formler.

Signatur

Angir mengden av konstant-, funksjons- og relasjonssymboler for et førsteordens språk.

⟨konstantsymboler; funksjonssymboler; relasjonssymboler⟩

Mengden av førsteordens termer

Basismengden består av alle konstant og variabel symbolene.

Induksjonssteget er hvis t1, …, tn er termer og f er en funksjon med aritet n, så er f(t1, …, tn) en term

Mengden av førsteordens formler

Basismengde består av alle atomære formler

Hvis F og G er formler, så er ¬𝐹, 𝐹 ∧ 𝐺 , (𝐹 ∨ 𝐺) og (𝐹 → 𝐺) formler

Hvis F er en formel og x er en variabel, så er r ∀𝑥𝐹 og ∃𝑥F en formel

Bundet

I formlene ∀𝑥F og ∃𝑥F er alle forekomster av x i F bundet og innenfor skopet til kvantoren. En variabel er fri hvis den ikke er bundet. En formel er lukket hvis den ikke inneholder noen frie variabler.

Predikat

Et uttrykk som inneholder en eller flere plassholdere og blir til sant/usant når vi erstatter plassholdere med verdier

Modell

En modell består av en ikke-tom mengde kalt domenet |M| og en funksjon som tolker ikke-logiske symbolene

Lukket term

En term er lukket hvis den ikke inneholder noen variabler

Oppfyllbar lukket formel

Hvis det finnes en modell som gjør den sant

Kontradiktorisk lukket formel

Hvis det ikke finnes en modell som gjør den sant

Gyldig lukket formel

Dersom alle modeller gjør den sann

Falsifiserbar lukket formel

Dersom ikke alle modeller gjør den sann

Teori

En mengde med formler