Week 8 Data Analysis: Confidence Interval Estimation Techniques

Confidence Interval

Range estimating population parameter's value. Range estimating true population parameter. Range estimating population parameters value with known sample. Range estimating a population parameter with certainty.

Population Mean (μ)

Average of all values in a population. Average value of a population's data points.

Population Proportion (π)

Ratio of a specific characteristic in a population.

Sample Statistic

Value calculated from sample data.

Upper Confidence Limit

Highest value in a confidence interval. Maximum value of the confidence interval.

Lower Confidence Limit

Lowest value in a confidence interval. Minimum value of the confidence interval.

Width of Confidence Interval

Difference between upper and lower limits.

Sample Size (n)

Number of observations in a sample.

Standard Deviation (σ)

Measure of data variability in a population.

95% Confidence Interval

Interval where 95% of estimates fall and 95% of samples contain true parameter.

Interval Estimate

Range providing more information than point estimate. Range of values for estimating a population parameter.

Variability

Extent to which data points differ.

Extrapolation

Inferring population characteristics from sample data.

Statistical Confidence

Degree of certainty in statistical estimates.

Sample Mean (X)

Average value calculated from sample data.

Interval Estimate Example

Illustrates confidence interval based on sample data.

Cereal Box Example

Application of confidence interval in real-world scenario.

Confidence Interval Calculation

Formula: X ± Z * (σ/√n).

Correct Statement about μ

Interval accurately reflects population mean based on sample.

Point Estimate

Sample statistic estimating population parameter. Single value estimate of a population parameter.

Standard Error

Standard deviation of the point estimate.

Zα/2

Critical value for normal distribution at α/2.

Level of Significance (α)

Probability of rejecting true null hypothesis.

Common Confidence Levels

Typical levels include 90%, 95%, and 99%.

Z-value for 95%

Zα/2 equals 1.96 for 95% confidence.

Population Standard Deviation (σ)

Measure of population data spread, can be known.

Confidence Coefficient

Probability that the confidence interval contains μ.

Sampling Distribution of the Mean

Distribution of sample means from repeated samples.

Confidence Interval Formula

Point Estimate ± (Critical Value)(Standard Error).

Example Calculation

Determine interval using sample mean and standard deviation.

Population Standard Deviation

Measure of variability in a population, σ.

95% Confidence Level

Probability that interval contains true mean.

Degrees of Freedom (df)

n - 1; number of free observations.

Sample Standard Deviation (S)

Estimate of population standard deviation from sample.

Normal Distribution

Symmetrical distribution where mean equals median. Probability distribution symmetric about the mean.

Critical Value (tα/2)

t value for specified confidence level and df.

Large Sample Size

n > 30; allows normal approximation.

William Gosset

Developed t distribution under pen name 'Student'.

Fat Tails

t distributions have heavier tails than normal.

Confidence Interval for μ (σ Unknown)

Uses t distribution when σ is not known.

t Table

Reference for critical t values based on df.

Standard Normal Distribution

Normal distribution with mean 0 and sd 1.

Random Sample

Subset of population selected without bias.

α Level

Significance level; probability of error.

t (df = ∞)

Standard normal distribution as sample size increases.

Sample Mean (X̄)

Average of values in a sample. Average value from a sample.

Confidence Interval Estimate Formula

X̄ ± tα/2 * (S/√n).

Degrees of Freedom (d.f.)

Calculated as sample size minus one (n - 1).

t Distribution

Used for estimating population parameters with small samples. Used when population standard deviation is unknown.

Normal Distribution Assumption

Population must be approximately normal for valid intervals.

Normal Probability Plot

Graphical tool to assess normality of data distribution.

Boxplot

Visual representation of data distribution and outliers.

Sample Proportion (p)

Proportion calculated from sample data.

Standard Normal Value (Zα/2)

Critical value for desired confidence level.

Confidence Interval Endpoints

Upper and lower limits of the confidence interval.

Sampling Error

Imprecision in estimating population parameters.

Margin of Error (e)

Amount added/subtracted to point estimate for interval.

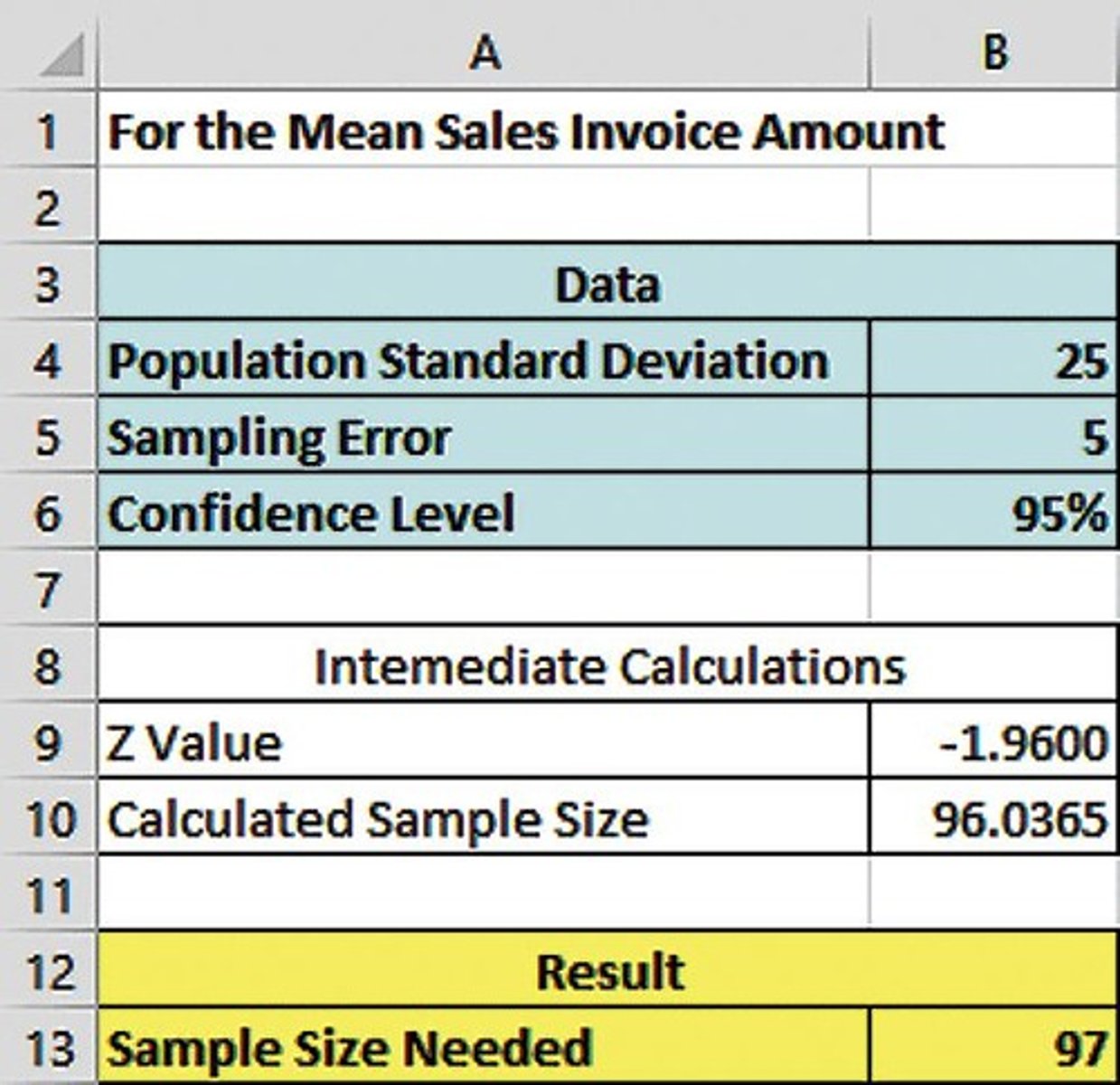
Required Sample Size (n)

Number of observations needed for desired accuracy.

Critical Value

Value used to determine confidence interval width. Table value based on desired confidence level.

Sample Size Formula for Mean

n = (Zα/2 * σ / e)².

Sample Size Formula for Proportion

n = (Zα/2² * p(1-p) / e²).

Pilot Sample

Initial sample used to estimate population parameters.

Confidence Level

Probability that the interval contains the true parameter. Percentage indicating interval reliability for parameter.

Left-Handed Proportion Example

Interval for left-handed individuals based on sample data.

Ethical Reporting

Include confidence intervals and sample sizes in reports.