Binomial Theorem

binomial coefficient

→ derived from r-combination

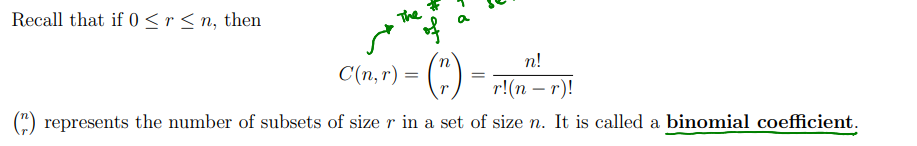
combinatorial proof + the two techniques

proof of the equality of two expressions

a combinatorial proof uses one of the two techniques:

• proof by double counting → counting the elements of a set in two diff ways

• proof by bijection → find a bijective function b/w two sets, thus showing the sets have the same CARDINALITY (same num of distinct elements)

pascal’s identity

• used to help build pascal’s triangle

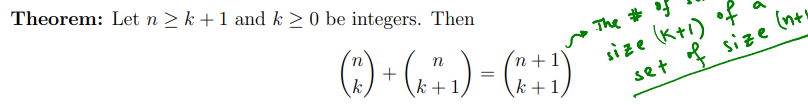
pascal’s triangle

• perfectly symmetrical

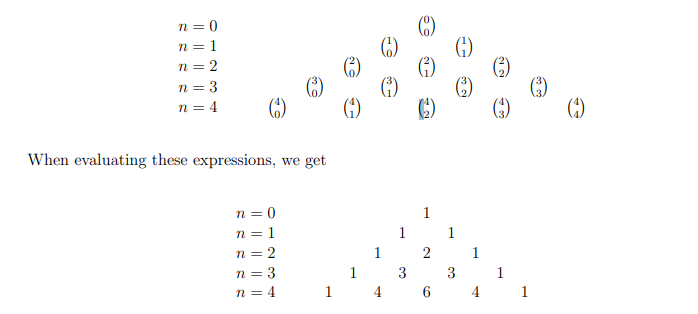
sum of the n’th row of the pascal’s triangle =

2^n

which is the same as the cardinality of the power set P(A) of a set A that contains n elements

binomial theorem formula

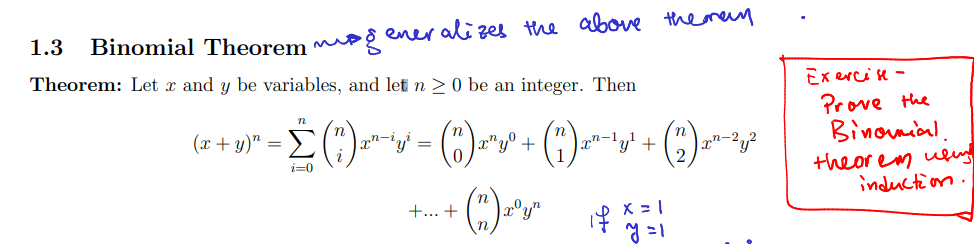
pigeonhole principle

if k + 1 objs or more are stored into k boxes, then at least ONE box contains two or more objs

generalized pigeonhole principle

if N objs are stored into k boxes, then at least one box contains at least N/k objs (bc N objs are unevenly or evenly divided into k groups)