Stats Unit 6 Probability

Confidence Interval Testing (p̂)

1. State the parameter of interest and the confidence level

2. Calculate Conditions

3. Find Z* for confidence

4. p̂+z*+standard deviation

Interpret Confidence Interval

We are % confident that the true (parameter) is between (bound) and (bound)

Interpret Confidence Level

If we were to repeat this process many times, about % of the confidence intervals we create would contain the true [parameter]

Hypothesis Testing (H₀ & Hₐ) (α,)

1. State (H₀ & Hₐ)

2. Check Conditions

3. Determine the Test Statistic

4. Find the P-Value so If p-value < α, reject H₀

5. Conclude

One-Proportion Z-Test H₀ & Hₐ)

1. Hypotheses H₀ & Hₐ)

2. Test Statistic (z-score)

Type I Error(α)

Rejecting H₀ when it’s true

Probability = α

Type II Error

Saying H₀ is true, when it’s false

Probability = β

Power of a Test

The probability of correctly rejecting H₀ when H₀ is false

Power = 1 - β.

Increased by larger sample size, higher α, and stronger effect size

Finding Sample Size

n=z² * p * (1-p)/E²

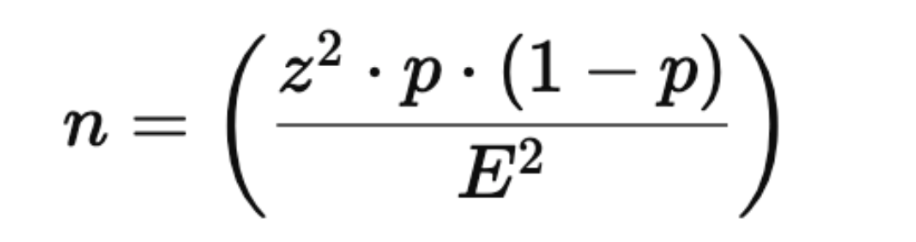
The point estimate

Midpoint of the confidence interval, calculated as (upper bound + lower bound) / 2

The margin of error

Distance between the point estimate and either the upper or lower limit of the confidence interval (upper boundary - point estimate)

How margin of error can be changed

Increase sample size → Decreases ME

• Square Root (original/change)

Increase confidence level → Increases ME

Increase variability → Increases ME