Herhalen - Alles - 24/06

Bespreek “Occam's scheermes” ivm modelselectie.

=> Ook bekend als het principe van spaarzaamheid

Occam's scheermes is een principe dat stelt dat, gegeven meerdere verklaringen voor een fenomeen, de eenvoudigste (met de minste aannames of parameters) de voorkeur verdient. In het kader van modelselectie betekent dit dat we eenvoud verkiezen, zolang het model nog goed past bij de data.

Motivatie:

• Esthetiek: eenvoudige theorieën/modellen zijn gemakkelijker uit te leggen en te begrijpen.

• Empirisch: werkt in de praktijk (evolutietheorie, Newtoniaanse mechanica, relativiteit, kwantumfysica).

• Statistisch: minder parameters, dus gemakkelijker te schatten!

Komt op natuurlijke wijze voort uit een Bayesiaans standpunt.

• Modellen met veel parameters krijgen een lagere marginal likelihood, tenzij de extra complexiteit significant bijdraagt aan de verklaring van de data.

Wat betekent het als je model “overfit” op je data en wanneer komt het voor?

Overfitting:

• Het model is te complex en leert niet alleen de echte patronen, maar ook ruis en toevallige details.

• Wanneer komt het voor?

  • Als het model te complex is (bv. veel parameters t.o.v. het aantal observaties).

  • Als er te weinig trainingsdata is.

  • Als er geen goede regularisatie wordt toegepast.

  • Als het model te lang getraind wordt zonder evaluatie op een validatieset.

• Vermijden door:

  • Cross-validatie, regularisatie (zoals L1/L2), en het kiezen van een model met gepaste complexiteit.

Underfitting:

Het model is te simpel en mist belangrijke patronen in de data

Geef 1 voordeel en 2 nadelen van een model complexer te maken

Voordelen:

• Realistischer zijn en specifiekere voorspellingen doen

• Meer gedetailleerde informatie over het systeem weergeven

Nadelen, vergeleken met eenvoudige modellen:

• Vereisen ze meer gegevens om te kalibreren en valideren

• Zijn ze moeilijker te begrijpen

• Zijn ze computationeel kostbaarder

Geef de formule voor de Bayes factor voor modelselectie. Hoe interpreteer je de waarde hiervan?

De Bayes factor wordt gebruikt om twee modellen M1​ en M2​ te vergelijken op basis van hoe goed ze de data verklaren.

Vergelijken van 2 modellen (M₂ vs. M₁) kan gedaan worden via de Bayes factor:

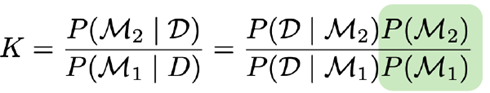
→ De gearceerde term kan geschrapt worden als er geen voorkeur is.

Interpretatie:

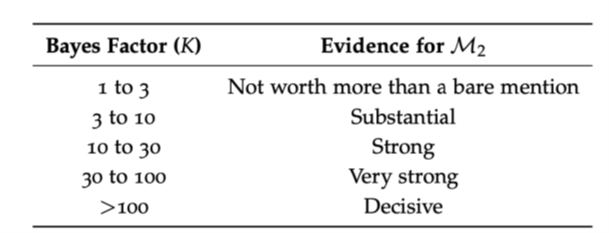
• Als K₂₁  > 1 , dan ondersteunt de data model M2​ meer dan model M1.

• Hoe groter K₂₁​, hoe sterker het bewijs voor M2

• Omgekeerd: K₁₂  = 1/K₂₁ ​, dus een klein getal (< 1) wijst in het voordeel van M1.

Jeffreys' schaal (vuistregel voor interpretatie):

Bespreek hoe de model evidence (P(D|M)) gebruikt kan worden voor Bayesiaanse modelselectie. Waarom is dit moeilijk te schatten?

De model evidence P(D∣M), ook wel marginale likelihood genoemd, is de kans op de data onder een bepaald model M. In Bayesiaanse modelselectie wordt het gebruikt om modellen te vergelijken.

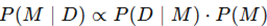
Wanneer we modellen een gelijke prior P(M) geven, bepaalt P(D∣M) direct welke modellen beter worden ondersteund door de data.

• We merken op dat P(D|M), het modelbewijs, de sleutel is voor modelselectie (gemakkelijk om te zetten in P(M|D) met behulp van de regel van Bayes).

• Tot nu toe hebben we er veel moeite voor gedaan om dit niet te berekenen (sampling, MAP…).

  • MAP/MLE geeft alleen de beste waarde van de distributie, niet de spread!

Idee: gebruik samples van een voorwaardelijke keten, samples van P(θ|D,M) en bereken

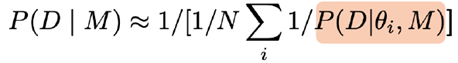
De gearceerde term is de likelihood

Dit wordt de ‘slechtste Monte Carlo-schatter ter wereld’ genoemd

Het berekenen van het modelbewijs kan worden gedaan door de posterior te benaderen, bijvoorbeeld met behulp van de methode van Laplace. We zullen informatiecriteria gebruiken als alternatief.

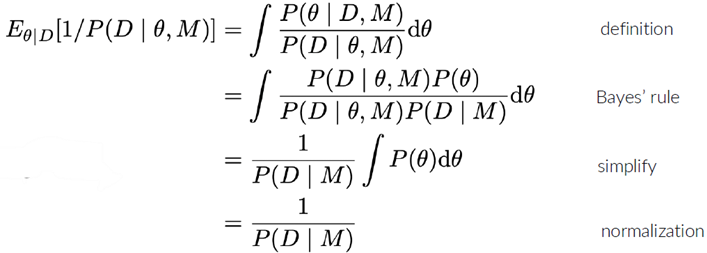
Geef en verklaar de formule voor AIC/BIC en hoe je die kan gebruiken voor modelselectie.

Zowel het Akaike-informatiecriterium (AIC) als het Bayesiaans informatiecriterium (BIC) zijn methodes om modellen te vergelijken op basis van hun fit aan de data én hun complexiteit.

Ze zijn gebaseerd op een benadering van het Bayesiaans modelbewijs en dienen als praktische alternatieven voor volledige Bayesiaanse integratie.

Akaike-informatiecriterium (AIC):

• Formule:

  

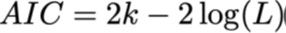
  • L = likelihood van het model gegeven de data

  • k = aantal vrijheidsgraden (parameters, incl. ruis)

  • n = aantal data-observaties

• Verklaring:

  • −2⋅logL meet hoe goed het model de data verklaart (lagere waarde = betere fit).

  • 2k bestraft complexiteit: meer parameters = straf.

• AIC is een praktische metriek voor modelselectie.

• Het brengt fit (waarschijnlijkheid L) en het aantal parameters k (inclusief die voor de ruisverdeling!) in evenwicht.

• Afleiding op basis van de Laplace-benadering.

• Geldig als:

1. Priors vlak/gedomineerd door waarschijnlijkheid zijn

2. Posterieur ongeveer normaal is

3. Steekproefomvang groot is: n >> k

• We kunnen zien dat de AIC gebruikt kan worden voor het berekenen van posterieure modelwaarschijnlijkheid:

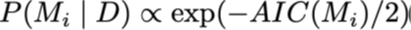
Bayesiaans informatiecriterium (BIC):

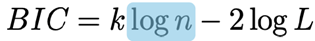
• Is vergelijkbaar, maar verkregen door een andere afleiding en aannames

• Hoe groter je dataset, hoe belangrijker het is om modelcomplexiteit te beperken om overfitting te voorkomen.

• Hier: k*log(n)  bestraft complexiteit: meer parameters = straf.

Reflecties op de informatiecriteria:

• Zowel AIC als BIC zijn niet erg betrouwbaar, maar ze zijn gemakkelijk te berekenen…

• Beter: gebruik het Watanabe-Akaike-informatiecriterium (WAIC)

  • Gebruikt de volledige posterieure keten van parametermonsters

  • Genereert een out-of-sample voorspellende nauwkeurigheid voor elk punt

Gebruik voor modelselectie:

• Vergelijk de AIC- of BIC-waarden van verschillende modellen.

• Lager = beter.

• AIC kiest vaak complexere modellen dan BIC.

• AIC is meer voorspellingsgericht, BIC is meer waarschijnlijkheidsgericht.

Geef de drie bronnen van onzekerheid in een wiskundig model.

• Input en parameter onzekerheid

• Structurele onzekerheid

• Numerieke onzekerheid

Leg het verschil uit tussen aleatorische en epistemische onzekerheid. Geef een voorbeeld. Hoe kan je die reduceren? Hoe modelleren we die?

Aleatorische onzekerheid = ruis.
Inherente willekeurigheid als gevolg van natuurlijke variaties, ruis en stochasticiteit. (Gaat over experimenten die je kan herhalen en er zullen bepaalde dingen veranderen.)

Kan je enkel reduceren door het systeem te verbeteren, NIET door meer data of beter modellen.

Wordt gemodelleerd via SDE’s, SSA’s, measuremnet noise, …

Epistemische onzekerheid  = kennis
Onzekerheid door het gebrek aan kennis of informatie. (gaat over dingen die je niet weet)

Kan gereduceerd worden door experimenten te doen of literatuur te bekijken (meer kennis op doen)

Wordt gemodelleerd via een Bayesiaans model

Wat zijn de stappen van een onzekerheidsanalyse? Leg elke stap kort uit.

1) Onzekerheid kwantificatie: identificeer alle bronnen van onzekerheid en kwantificeer ze door                                        gebruik te maken van distributies, betrouwbaarheidsintervallen, …

2) Onzekerheid propagatie: analyse van hoe de onzekerheden in de input van het model effect hebben op de onzekerheid van de output van het model.

3) Onzekerheid toeschrijven: individuele contributies van onzekerheid linken aan de verschillende bronnen

Geef en bespreek de twee manieren die we gezien hebben om onzekerheidspropagatie te doen. 

1) Lineaire error propagatie:
Stochastische variabele X wordt weergegeven door enkel zijn gemiddelde en standaard fout µ_x+/-. Het is minder computationeel intensief dan Monte Carlo.
Stel dat X en Y onafhankelijk zijn, dan:

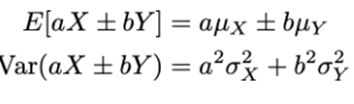
Als ze gecorreleerd zijn:

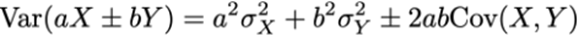
2) Niet lineaire error propagatie
voor niet lineaire functies kunnen we een Taylor benadering gebruiken

Voor variantie:

 

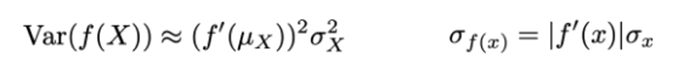
Reken met een getal met meetfout: som/verschil van twee fouten en eenvoudige niet-linaire transformatie. 

Leidt de benaderde waarde voor de gemiddelde en standardafwijking van een functie-evaluatie f(X) van een stochastische variabele aan de hand van een eerste-orde Taylor

→ Dit maar dan op eerste orde benadering toegepast

Wat is het verschil tussen lokale en globale sensitiviteitsanalyse? 

• Lokale sensitiviteit = hoe groot is de impact van een verandering in input/parameter op de output (hoeveel verandert je output als je de input verandert)

• Globale sensitiviteit = globaal begrip van hoe verschillende regio’s van de input/parameter ruimte de output van het model beïnvloeden (connectie tussen verschillende parameters)

Gegeven een onderzoeksvraag en modelbeschrijving, geef drie  voorbeelden van waarvoor een sensitiviteitsanalyse nuttig kan zijn. 

Redenen voor een sensitiviteit analyse:

• Belangrijke inputs t.o.v de output identificeren

  • Data collectie

  • Onzekerheid kwantificatie

• Simplificatie van het model (inputs wegdoen die geen effect hebben op de output)

• Robuustheid testen (hoe verandert de output als de input verandert)

• Keuze ondersteuning en communicatie

• Experimenteel design

Geef de formule voor de (niet-)genormaliseerde lokale sensitiviteitsindex

Lokale sensitiviteit index:  

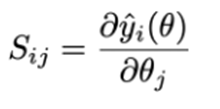
Relatieve lokale sensitiviteit index (genormaliseerd):

 

 

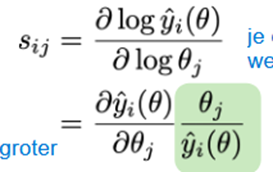
Bereken de (genormaliseerde) sensitiviteitsindex van een functie (bv. michaelis menten)

Wanneer zou je de absolute error als loss functie gebruiken i.p.v. de kwadratische fout (squared error)?

Bij optimalisatie proberen we om een model te verkrijgen dat goed aansluit bij de gekregen data, het doel is om de fout tussen deze voorspelde waarden ^yi en de werkelijke waarden yi te minimaliseren:

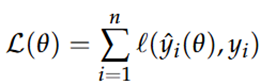
We hebben verschillende opties voor de loss functie:

De kwadratische fout (squared loss) is de populairste:

= het kwadraat van het verschil tussen de voorspelde & werkelijke waarde

• square problems (kleinste kwadraten problemen) zijn streng op grote modelafwijkingen, maar mild voor kleine

• telt outliers mee → outliers geven aanleiding tot grote foutwaardes

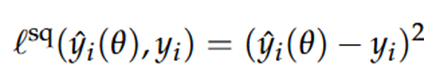
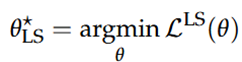
Absolute error

• telt geen outliers mee

• Bij deze methodes worden grote fouten enkel bestraft naar hun werkelijke grote (en dus niet gekwadrateerd)

• Bij deze methode tellen milde fouten meer mee dan bij least-squared

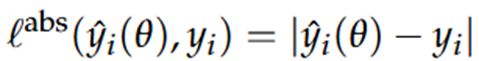
Hoe kan je een loss functie aanpassen zodat deze kan omgaan met heteroskedasticiteit?

Dan maken we gebruik van weighted loss:

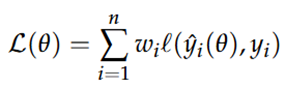
• Hierbij wordt de variantie van de fouten (residuen meegewogen), heteroskedasticiteit betekent namelijk dat de variantie van de fouten niet constant is (sommige waarnemingen hebben meer ‘ruis’ dan anderen)

• We voegen een gewicht toe → dit is de inverse van de variantie van de fout van een observatie

Gevolgen van deze weighted loss:

• Observaties met hoge variantie (veel ruis) krijgen een lager gewicht → de metingen met veel ruis krijgen een minder grote invloed

• Observaties met lage variantie (weinig ruis) krijgen een hoger gewicht

Geef een reden om wegingsfactoren in je loss functie in te bouwen. Hoe kies je de gewichten?

Redenen:

• Je kan dit doen als je verschillende variabelen meet (pH, temperatuur, OD) met elk hun eigen ruis en variabiliteit,

• of als er regio’s in tijd en ruimte zijn met hogere ruis

• of als sommige variabelen meer belangrijk zijn om juist te fitten dan andere

Hoe gewichten kiezen? Als de errors normaal verdeeld zijn met variërende varianties dan:

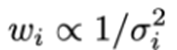
Wat houdt “regularisatie” in bij parameterkalibratie? Hoe wordt dit gedaan in het Bayesiaanse geval?

Regularisatie = techniek om te voorkomen dat een model overfit (te sterk gaat passen op ruis of toevalligheden in de data). Bij parameterkalibratie zorgt regularisatie ervoor dat de parameters:

• Niet te extreem worden

• Een voorkeur hebben voor eenvoud of bepaalde waarden (zoals nul of een vooraf bekende waarde)

→ via toevoeging strafterm: Loss = fouten + lambda*regularisatieterm

Bayesiaanse geval

→ via toevoegen van een prior (geeft aan wat we verwachten van parameters)

• Zowel een likelihood als een prior distribution P(θ) wordt gebruikt om de parameters in te schatten

• De posterior distributie wordt dan proportioneel aan de prior & de likelihood:

  

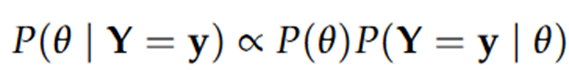
• Dit is slechts proportioneel omdat we normaal nog moeten delen door P(Y = y) (de kans op de data over alle mogelijke parametercombinaties), maar dit wordt vaak weggelaten omdat dit erg moeilijk te berekenen is & toch enkel zorgt voor een herschaling

Geef wiskundig en intuïtief wat de Fisher informatie zegt over een loss functie (eventueel met een schets). Waarvoor wordt dit gebruikt bij parameterkalibratie?

Een MLE schatting ligt altijd in een minimum (punt met de hoogste likelihood). In een MIN is de 1e afgeleide gelijk aan nul. Nu willen we weten of het kiezen voor een parameterinschatting θ^* in plaats van de geoptimaliseerde θ een groot effect heeft op onze negative log-likelihood. Dit hangt af van de helling van het minimum waar θ^* in ligt.

→ Steile helling → verandering van θ heeft een groot effect

Omdat de 1e afgeleide geen informatie oplevert, moeten we kijken naar de 2e afgeleide. De helling van de log-likelihood noemt men de Fisher information:

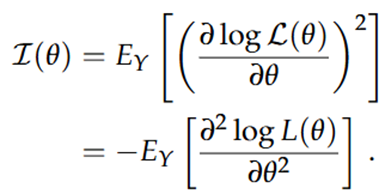
Deze waarde is echter vaak moeilijk te berekenen, waardoor we gebruik maken van geobserveerde informatie:

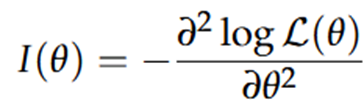
Grote hellingen van de log-likelihood functie betekenen een meer precisie inschatting van θ. Wanneer we veel data hebben is de kromming vaak groter (het maximum is beter gekarakteriseerd & de parameter kan beter geschat worden).

• Log-likelihood is scherp rond het MAX → kleine verandering in θ zorgt voor een grote verandering in de likelihood → veel informatie → hoge Fisher-informatie

Volgende schets kan gemaakt worden (p165):

In parameterkalibratie wordt dit gebruikt voor:

• Onzekerheidsschatting → meer informatie leidt tot minder onzekerheid

• We meten de data op een manier die de Fisher-informatie maximaliseert (om dus de meest informatieve data te verzamelen)

• Kan ook gebruikt worden om informatieve priors te bouwen

Waarvoor gebruik je een Laplace benadering bij parameterkalibratie? Leg uit hoe het werkt.

Een tweede manier om de 2e afgeleide aan de log-likelihood (of log-posterior voor MAP) te linken is door de Laplace benadering. Hierbij proberen we om een posteriorverdeling van parameters te benaderen met een normale verdeling. De voordelen hiervan zijn: (1) de exacte posterior heeft vaak geen mooie vorm, terwijl een normale verdeling dit wel heeft. (2) Een normale verdeling is rekenkundig eenvoudiger & (3) je krijgt direct schattingen van onzekerheid van de parameters.

De werking:

1. Stel we hebben een posteriorverdeling van parameter θ met de MAP (maximum a posteriori punt) θ^* (punt waar de posterior het grootst is)

2. We kunnen de log-posterior benaderen met een 2e orde Taylor reeks rond θ^*

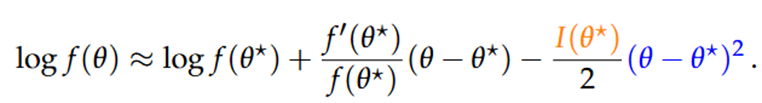
a. De tweede term valt weg want de eerste afgeleide is gelijk aan nul

b. Bij de derde term gebruiken we meteen de Fisher informatie ipv de tweede afgeleide

3. Als we dit vergelijken met de PDF van een normale verdeling, zijn de eerste termen constant (kunnen gezien worden als genormaliseerde constanten). We kunnen dus de kwadratische uitdrukking voor de posterior uitdrukken als een normale distributie:

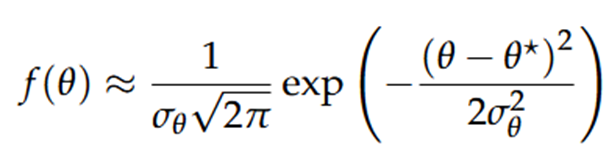
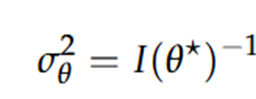
→ De Laplace-benadering een multivariate normale verdeling met de gemiddelde vector θ^* en, als covariantiematrix, de inverse Hessiaan van de log-PDF.

Gegeven een ongenormaliseerde posterior distributie, geef de lokale normale benadering a.d.h.v. de Laplace benadering.

• Eerste stap: vinden van het MAP punt (dit is het maximum van de ongenormaliseerde posterior distributie)

• Tweede stap: neem een 2e orde Taylor-reeks van de log-posterior rond θ^* (zie stap 2 van de werking voor de formule)

  • Hiermee benaderen we de log-posterior lokaal als een parabool

• Derde stap: logaritme omzetten naar de posterior zelf, door de exponent van beide kanten te nemen

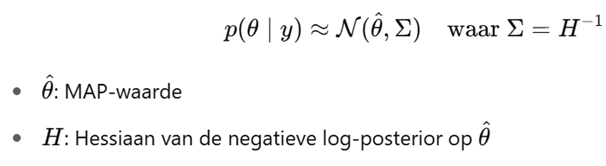
→ Dan verkrijgen we de vorm van een multivariate normale verdeling

Hoe maak je van een maximalisatie probleem een minimalisatie probleem?

in plaats van een functie g(*) te maximaliseren, kunnen we ook de doelfunctie -g(*) minimaliseren.

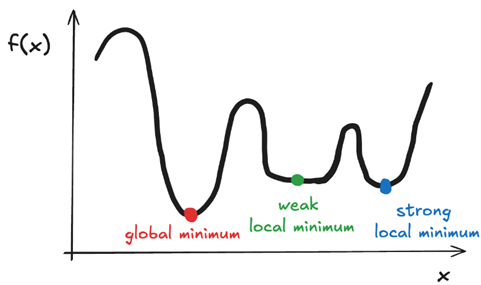
Gegeven een grafiek van een loss functie, duid de verschillende soorten minima
aan en leg uit waarom dit een probleem kan vormen bij optimalisatie.

Bij een optimalisatieprobleem zoeken we naar het globaal minimum van een lossfunctie, omdat dit het punt is waar de loss (of fout) het kleinst is over het hele domein van de functie. Echter, veel functies, vooral in machine learning en niet-lineaire optimalisatie, zijn niet-convex, wat betekent dat ze meerdere minima (en maxima) kunnen hebben. Daardoor kunnen we ook terechtkomen in:

• Globaal maximum

• Lokaal maximum

• Globaal minimum

• Lokaal minimum.

Verder wordt er nog een onderscheid gemaakt tussen:

• Sterk lokaal minimum → minimaliseert de functie in de omgeving

• Zwak lokaal minimum → meerdere punten in de omgeving met dezelfde minimale waarde (bv. een vlakke lijn of plateau als minimum)

Optimalisatie-algoritmen zoals gradient descent kunnen vastlopen in een lokaal minimum als het startpunt slecht gekozen is. Ze ‘zien’ alleen de lokale structuur van de functie en kunnen daardoor het globale minimum missen. Dit is vooral problematisch bij complexe functies met veel plooien, zoals in deep learning.

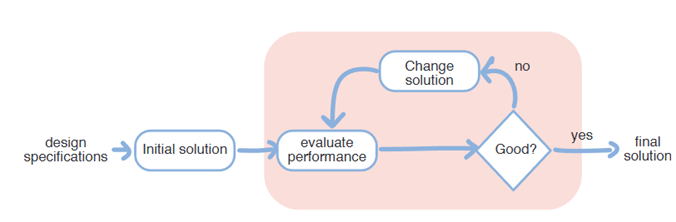
Teken de algemene optimalisatie cyclus uit.

Bespreek het verschil tussen grid search en random search / Monte Carlo optimalisatie. Wat zijn hun respectievelijke voor-en nadelen?

Eerste optie: grid search

Principe: het interval van een parameter wordt opgedeeld in gelijke segmenten. In elk segment wordt één of meerdere punten geëvalueerd, en men kiest het segment waarin de waarde van de doelfunctie het laagst is.

• Voor optimalisatie over een interval [a, b] verdeelt grid search het interval over (equidistante) punten, die allemaal worden geëvalueerd. We behouden degene met de laagste objectieve waarde

  • Goed bij klein interval [a,b]

  • Logaritmische segmenten bij groot interval

• over meerdere parameters is mogelijk → grid search over vlak (x-as = segmenten 1e parameter, y-as = segmenten 2e parameter)

  • curse of dimentionality Hoe meer parameters → hoe sneller het aantal te evalueren combinaties toeneemt

• Eenvoudig te implementeren!

• Omdat slechts een beperkt aantal punten per parameter wordt geëvalueerd, bestaat de kans dat de globale minimizer niet geëvalueerd wordt. Hierdoor is de methode biased en mogelijk suboptimaal

Tweede optie: random search / Monte Carlo optimalisatie

Principe: we genereren willekeurige waarden uit een kansverdeling over het parameterinterval. Deze punten worden vervolgens geëvalueerd om het minimum te vinden.

• Sample kandidaatwaarden uit het interval [a, b] volgens een bepaalde verdeling, bv. uniform

• Eenvoudig te implementeren en triviaal te paralleliseren

• Deze methode heeft geen bias aangezien elke waarde mogelijk is, maar het kan regio's missen door toeval (hoge variantie!)

• Gebruik een andere sampling-distributie als er voorkennis van de minimizer beschikbaar is

  • Hierbij kunnen we voorkennis over het minimum verwerken in de distributie: indien vermoed wordt dat het minimum zich rond een bepaalde waarde bevindt, kan gekozen worden voor een normale verdeling gecentreerd rond dat punt.

• Voor hogere dimensie optimalisatie-problemen maken we gebruik van meerdere distributies, dit kan op twee manieren:

  • Distributies samenbrengen via de product distributie (zie vraag 60)

  • Turing model opstellen in julia

→ Random search is vaak efficiënter in hoge dimensies, omdat het geen volledig rooster moet doorlopen, maar toch representatief kan bemonsteren

Aspect	Grid Search	Random Search/ Monte Carlo
Systematiek	Gestructureerd, deterministisch	Willekeurig, probabilistisch
Efficiëntie in lage dimensies	Goed	Goed
Efficiëntie in hoge dimensies	slecht (curse of dimensionality)	Beter (sneller representatief)
Bias	Ja, vaste punten kunnen global optimum missen	Nee, elk punt heeft gelijke kans
Voorkennis integreren	Moeilijk	Mogelijk via aangepaste distributies
Aspect	Grid Search	Random Search/ Monte Carlo
Herhaalbaarheid	Hoog (zelfde rooster → zelfde resultaten)	Lager (tenzij random seed wordt gefixeerd)

Extra: stratified sampling → hierbij worden de twee methoden samengenomen: initieel wordt het interval opgedeeld in segmenten (of een vlak) & in deze segmenten worden random waarden gesampled om te evalueren.

Geef de algemene update regel voor gradiënt-gebaseerde optimalisatie methoden en bespreek de delen.

Gradiënt-gebaseerde optimalisatie is een iteratief proces waarbij een functie f(x) wordt geminimaliseerd door bij een beginpunt x⁰ telkens in de richting van de steilste daling te bewegen.

 

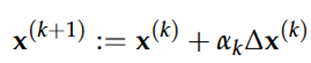
• x^(k) = huidige oplossing bij stap k van de optimalisatierun

• ∆x^(k) = de zoekrichting: vector die wijst in de richting waarin we zullen stappen

• α_k = de stapgrootte (= learning rate): een scalair die bepaalt hoe ver we in de zoekrichting gaan

•      => Dit is een iteratief proces waarbij we bij x⁰ beginnen, om dan via een reeks optimalisatiestappen uit te komen bij een waarde waarvoor geldt:

 

\left|\nabla f\left(x\right)\right| < epsilon

 

• Dit is het stopcriterium

• Hierbij is ε een vooraf bepaalde tolerantie die bepaalt wanneer we voldoende dicht bij een lokaal (of globaal) minimum zijn

• Het bepalen van de zoekrichting & de stapgrootte geeft aanleiding tot verschillende optimalisatiemethoden

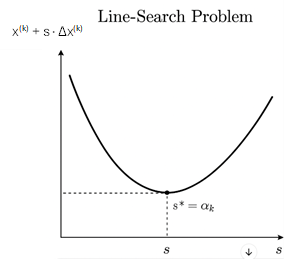
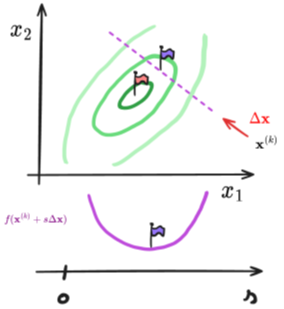
Wat is een "line-search" probleem bij optimalisatie? Schets een grafiek van het probleem

Wanneer de zoekrichting gegeven is, kunnen we de optimale stapgrootte vinden door volgend line search probleem:  

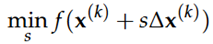
• Bij elke stap moet men een 1D-lijnzoekprobleem oplossen om de optimale stapgrootte α te vinden (via formule hierboven)

• Hierbij is s een scalair die de stapgrootte voorstelt.

• De optimale oplossing s* komt overeen met de ideale stapgrootte α_k.

Verschillende strategieën voor het kiezen van de zoekrichting en stapgrootte leiden tot verschillende optimalisatiemethoden.

De verschillende oplossingsmethoden:

• Exacte oplossing van s* bepalen

• Benaderende oplossing → line-search algoritmes zoeken een benadering voor s*

  • Hoe accurater, hoe meer het kost & hoe langer het duurt

• Gebruik makend van een vervalreeks, zoals α_k = 1/(c+k)

• Gebruik makend van een constante stapgrootte α_k

Geef de Newton stap, bespreek de convergentie. Wat is het (computationeel) nadeel van deze methode?

De Newton stap (afleiding p142) geeft de richting & grootte van de optimale stap, gebaseerd op de 2^e orde Taylor benadering van f(x). Dit leidt tot kwadratische convergentie dicht bij het optimum (op voorwaarde dat de Hessiaan positief-definiet is).

 

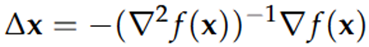
·        ∇f(x) → de gradiëntvector (eerste afgeleiden)

·        ∇²f(x) → de Hessiaan (matrix van tweede afgeleiden)

·        (∇²f(x))^-1 → de inverse van de Hessiaan, deze bepaalt hoe we de gradiënt heroriënteren

·        Het minteken duidt aan dat we bewegen in de richting van de daling

Karakteristieken:

·        Efficiënt voor hogere dimensieproblemen

·        Redelijk ongevoelig voor imperfecte stapgroottes (de richting is belangrijker dan de grootte)

·        ‘affine invariant’ → rotatie of translatie van het coördinatenstelsel beïnvloedt het gedrag van het algoritme niet

De convergentie gebeurt vaak in twee fasen:

• Damped Newton phase

  • Komt voor als α_k < 1

  • De convergentie is lineair: log(f(x^(k) – f(x*)) daalt met een constant tempo per iteratiestap

• Pure Newton phase

  • Als x^(k) dichtbij het minimum x* komt, wordt α_k = 1

  • De 2^e orde Taylor term benadert f(x) goed, we een kwadratische convergentie kennen.

  • Het aantal correcte cijfers in het antwoord verdubbelt bij elke iteratie.

Nadeel: bij elke iteratie moet een nieuwe (n x n) matrix worden berekend, opgeslagen & geïnverteerd. Voor grote problemen (bv n > 100) wordt dit computationeel zwaar (en soms onhaalbaar).

• Voor elke stap moeten we:

  • De Hessiaan berekenen en opslaan (n² elementen)

  • Die Hessiaan inverteren/systeem oplossen (O(n³))

 Dit probleem proberen we te omzeilen bij het gebruik van quasi-Newton methodes, waar de hessiaan benaderd wordt.

Leg in één zin uit welk probleem quasi-Newton algoritmes oplossen tegenover de originele Newton methode. Wat zijn direct-search/nulde-orde optimalisatiemethoden? Besprek bondig hoe de Nelder-Mead methode werkt en wanneer je het wel of niet zou gebruiken.

a) Leg in één zin uit welk probleem quasi-Newton algoritmes oplossen tegenover de originele Newton methode.

Quasi-Newton algoritmes vermijden de dure berekening en inversie van de Hessiaanmatrix door deze iteratief te benaderen, wat ze veel efficiënter maakt voor grote problemen.

b) Wat zijn direct-search / nulde-orde optimalisatiemethoden?

Dit zijn optimalisatiemethoden die geen afgeleiden gebruiken, maar enkel waarden van de objectieffunctie f(x).

·        Vertrouw uitsluitend op functie-evaluaties (f(x)), niet op afgeleiden.

·        Iteratief verbeteren van oplossingen zonder gradiëntinformatie → gepast voor problemen waar de gradiënt niet gekend is, of moeilijk te berekenen is

·        Stopcriterium: wanneer er geen verdere verbetering wordt waargenomen (we gebruiken dus geen gradiënt als stopcriterium)

c) Bespreek bondig hoe de Nelder-Mead methode werkt en wanneer je het wel of niet zou gebruiken.

Gedeeld document:

Nelder-Mead (NM) is een direct search methode die werkt met een simplex — een geometrisch figuur met n+1 hoekpunten in n dimensies. In elke iteratie worden de functiewaarden geëvalueerd in elk hoekpunt, waarna de slechtste wordt vervangen via één van vier mogelijke acties:

·        Reflecteren: spiegeling over het zwaartepunt → het punt met de hoogste waarde wordt gereflecteerd over het zwaartepunt waardoor het slechtste punt wordt weggewerkt

·        Expanderen: uitbreiding richting het beste punt → het beste punt wordt verder weggebracht zodat de simplex expandeert

·        Contracteren: samentrekking richting betere punten → de simplex krimpt doordat het weg-beweegt van het slechtste punt

·        Krimpen: alle punten worden dichter bij het beste punt gebracht

Het algoritme stopt wanneer de variatie (standaardafwijking) tussen functiewaarden onder een drempel ε zakt.

NM is simpel om te implementeren, robuust & computationeel efficiënt voor lage dimensieproblemen. Bij hogere dimensieproblemen of functies met een lokaal minima kan het vastlopen.

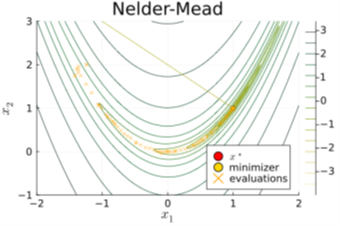
Uit samenvatting:

·        Populaire directe (nulde-orde) optimalisatiemethode

·        Werkt zonder gradiëntinformatie, ideaal voor complexe/onbekende functies

·        Werkt op een "simplex": een geometrische vorm met n+1 hoekpunten in n dimensies

·        Initiële simplex wordt gevormd, functiewaarden worden bij elk hoekpunt geëvalueerd

Bewerkingen en iteratie:

Vier hoofdbewerkingen op de simplex:

·        Reflectie: Reflecteer het slechtste punt over het zwaartepunt

·        Uitbreiding: Breid de reflectie uit om verder te verkennen

·        Contractie: Krimp de simplex richting het zwaartepunt

·        Krimp: Krimp de hele simplex richting het beste punt

De hoekpunten worden gesorteerd van de laagste (beste) tot hoogste (slechtste) objectieve waarden. Het slechtste punt wordt altijd vervangen door een potentieel beter punt, dat de simplex dichter naar het minimum zou kunnen verplaatsen. De grootte en vorm van de simplex passen zich aan de vorm van de functie aan die wordt geminimaliseerd.

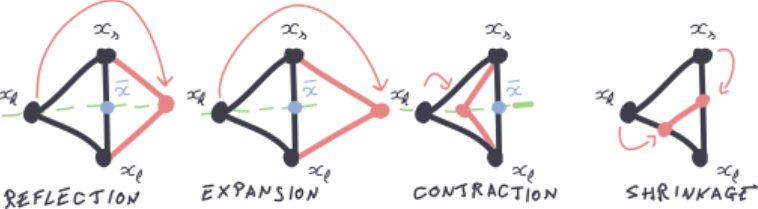
Deze methode is makkelijk te implementeren, is efficiënt voor laag-dimensionele problemen en is relatief robuust. Voor hoog-dimensionele problemen kan het minder efficiënt zijn.

Hoe verschillen populatie-gebaseerde optimalisatiemethoden van andere methoden die hun oplossing iteratief verbeteren?

Populatie-gebaseerde optimalisatiemethoden werken met een verzameling (populatie) van potentiële oplossingen, in plaats van één enkele oplossing die iteratief wordt aangepast.

·        In elke iteratie wordt de hele populatie geëvalueerd, en worden nieuwe oplossingen gegenereerd

·        Ze maken gebruik van de collectieve intelligentie van de populatie om de zoekruimte te verkennen

·        Ze hebben de mogelijkheid om complexe interacties binnen hoog-dimensionele datasets op te merken

·        Verminderen het risico om vast te lopen in lokale optima

·        Gebruik een aspect van willekeur om de zoekruimte te verkennen

·        Deze methoden zijn doorgaans minder vatbaar voor lokale minima, omdat meerdere oplossingen tegelijk worden verkend. (staat niet in samenvatting)

Voorbeelden (vaak biogeïnspireerd):

·        Genetische algoritmen (GA)

·        Optimisatie van deeltjeszwerm (PSO)

·        Optimalisatie van mierenkolonie (ACO)

Verschil met andere methoden:

·        Klassieke methoden (zoals gradient descent, Newton, quasi-Newton, Nelder-Mead) verbeteren één enkele oplossing iteratief.

·        Populatie-methoden gebruiken collectieve informatie van meerdere kandidaten, wat exploratie (brede verkenning) bevordert in plaats van louter exploitatie (lokale verbetering).

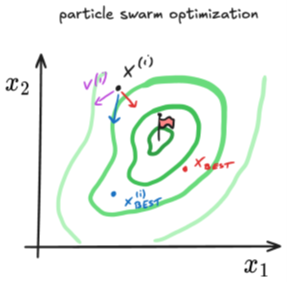
Geef het idee achter particle-swarm optimization (PSO). Geef de drie termen die de beweging van een individu beïnvloeden.

Hierbij beweegt een groep van communicerende partikels doorheen de zoekruimte. De posities van de partikels worden gezien als potentiële oplossingen & hun beweging wordt beïnvloed door (1) hun persoonlijk beste positie & (2) de beste positie van de groep.
Elke partikel i heeft een positie x⁽ⁱ⁾ en een snelheid v⁽ⁱ⁾, die worden geüpdatet door:

 

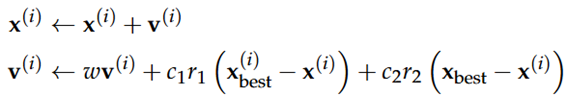
• x_best = de groep zijn beste positie en  = de partikel zijn beste positie

• w, c₁ en c₂ zijn parameters die de snelheid beïnvloeden, gewichten die zorgen voor een bais op de zoektocht

• r₁ en r₂ zijn twee random variabelen uit de uniforme distributie: Uniform(0,1)

De snelheid wordt beïnvloed door drie termen:

• 1^e term → momentum update, omdat w  [0,1] bewegen de partikels in dezelfde richting

  • Dit zorgt ervoor dat een deel van de voorgaande snelheid wordt bijgehouden & dit stimuleert exploratie

• 2^e term → aantrekking tot  

  • Aantrekking tot persoonlijk beste positie van deeltje

• 3^e term → aantrekking tot x_best

  • Trekt deeltjes toe naar globale beste positie

=> Balans tussen persoonlijke en globale informatie zorgt ervoor dat de zwerm kan convergeren naar optimale oplossingen.

PSO werkt goed in continue, gladde zoekruimtes met weinig ruis en maakt geen gebruik van afgeleiden (0^e orde).

Leg de Bayesiaanse denkwijze uit om een parameter te schatten. Wat zijn de vier distributies die hier een rol in spelen? Beschrijf ze elk aan de hand van een voorbeeld.

De Bayesiaanse denkwijze is een manier om informatie (zoals metingen of observaties) te combineren met bestaande kennis of overtuigingen (voorkennis) om een betere inschatting te maken van een onbekende parameter. In tegenstelling tot klassieke statistiek, die parameters als vaste maar onbekende waarden beschouwt, ziet de Bayesiaanse statistiek parameters als willekeurige variabelen waarover we onzekerheid hebben, en die we beschrijven met kansverdelingen.

Formule van Bayes:

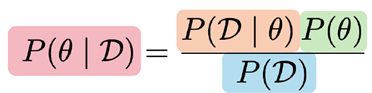
• P(D|theta) s de ‘likelihood’ verdeling: het geeft de kans van de data, gegeven de parameters

  • Dit is de kans op de geobserveerde data gegeven een specifieke waarde van de parameter. De likelihood komt uit je meetmodel of experiment.

  • Voorbeeld: Je meet de lengte van 10 mannen en krijgt een gemiddelde van 178 cm. Je model gaat ervan uit dat lengtes normaal verdeeld zijn met bekende standaarddeviatie. De kans op deze gegevens, gegeven een bepaald gemiddelde, is je likelihood.

• P(theta) is de prior, die onze overtuigingen en kennis over de parameters vertegenwoordigt voordat we de data waarnemen

  • Dit is je initiële overtuiging over de parameter voordat je gegevens hebt gezien.

  • Voorbeeld: Stel je wil de gemiddelde lengte van volwassen mannen in België schatten. Je weet van eerdere studies dat dit ongeveer 180 cm is, met enige variabiliteit. Je kiest dan bijvoorbeeld een normale priorverdeling met een gemiddelde van 180 cm en een standaarddeviatie van 10 cm

• P(D) is het modelbewijs, dat weergeeft hoe waarschijnlijk het is dat dit model of deze simulator deze data kan genereren over alle mogelijke waarden van de parameters

• P(theta|D) is de posteriorverdeling, die onze overtuigingen over de waarden van de parameters vertegenwoordigt, gegeven dat we data hebben waargenomen.

  • Dit is je bijgewerkte overtuiging over de parameter nadat je de gegevens hebt gezien.

  • Voorbeeld: Na het verwerken van je metingen (via Bayes’ regel), stel je vast dat de gemiddelde lengte waarschijnlijk iets lager is dan je aanvankelijke schatting. De posteriorverdeling is bijvoorbeeld normaal met gemiddelde 178,5 cm en een kleinere standaarddeviatie dan de prior (want je hebt nu extra informatie).

In woorden:
posterior = likelihood*prior/evidence

Leg het verschil uit tussen MLE en MAP.

Het verschil tussen MLE (Maximum Likelihood Estimation) en MAP (Maximum A Posteriori) ligt vooral in het gebruik van voorkennis (de prior)

MLE:

• MLE zoekt de waarde van de parameter θ die de waarschijnlijkheid van de waargenomen data maximaal maakt.

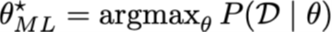
• Gebruik:

  • Alleen de likelihood wordt gebruikt — er wordt geen gebruik gemaakt van voorkennis of prior.

• Voorbeeld:

  • Stel je observeert 8 kop en 2 munt in 10 worpen van een munt.
    MLE zegt: wat is de kans θ(voor kop) die deze data het meest waarschijnlijk maakt? Antwoord: 8/10=0.8

MAP:

• MAP zoekt de waarde van θ die het meest waarschijnlijk is gegeven de data én je voorkennis

• Gebruik:

  • Zowel de likelihood als de prior worden meegenomen.

• Voorbeeld:

  • Je denkt vooraf dat de munt eerlijk is: P(θ) heeft een piek bij 0.5 (bijv. een Beta(5,5)-prior)

  • De MAP-schatting combineert de data met deze prior en komt misschien uit op θ^MAP=0.75, dus iets minder extreem dan MLE omdat je voorkennis tegenwicht biedt.

Samenvattend:

Kenmerk	MLE	MAP
Houdt rekening met prior?	Nee	Ja
Gebruikt	Alleen de data (likelihood)	Data én voorkennis (prior)
Doel	Waarschijnlijkste verklaring voor de data	Waarschijnlijkste waarde gegeven data én voorkennis
Kan gevoeliger zijn voor kleine datavolumes?	Ja	Nee (MAP is vaak stabieler met weinig data)

Wat is een prior distributie? Geef een voorbeeld.

= een kansverdeling die je gebruikt om je voorkennis of overtuiging over een parameter uit te drukken voordat je data observeert.

• In de Bayesiaanse statistiek = startpunt: wat denk je over de mogelijke waarden van de parameter, nog vóór je metingen of observaties hebt gedaan.

Voorbeeld:

Stel je wilt weten hoeveel mensen in een stad besmet zijn

• Hebt nog geen lokale data maar weet uit eerdere studies dat in vergelijkbare steden ongeveer 5% besmet is

• Dan kan je modelleren met een prior

Leg het verschil uit tussen een informatieve, zwak informatie en niet- informatieve/diffuse prior.

Er zijn drie categorieën, gebaseerd op hoeveel informatie ze bevatten:

• Informatief: sterke voorkennis, mogelijke bias (voor de posterior naar bepaalde waarden)

• Zwak informatief: erkent voorkennis, minder bias

• Diffuus/niet-informatief: minimale voorkennis, datagedreven

Gegeven een simpel voorbeeld van prior en likelihood (waarschijnlijkheid), bereken de posterior.

Bespreek voor een gegeven probleem of een Bayesiaanse aanpak aangewezen is of niet.

Vooral nuttig als er:

·        Weinig data beschikbaar is

·        Hebt voorkennis of expert-opinie

·        Wil een volledig beeld van onzekerheid

·        Wil modelupdating doen bij nieuwe data

In Bayesiaanse statistiek werken we vaak met ongenormalizeerde distributies. Waarom? Wat is de interpretatie van de normalizatieconstante?

Als je 1 variabele wilt conditioneren krijg je een ongenormaliseerde PDF van de conditionele distributie. In plaats van de normalisatieconstante (moeilijk te berekenen) te berekenen, zoeken we naar manieren om steekproeven uit deze verdeling te nemen en deze steekproeven te gebruiken om meer over de posterior te leren.
De normalisatieconstante Z is
 
met (x) de ongenormaliseerde  PDF. De normalisatie constante is een schaalfactor.

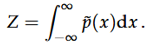
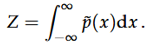
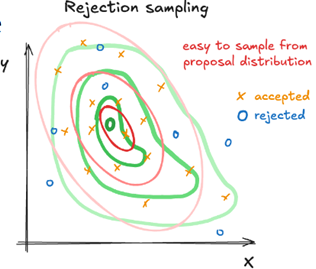
Leg uit hoe rejection sampling werkt aan de hand van een schets. Waarom schaalt dit niet naar hoog-dimensionele problemen?

Methode:

Grafiek: trek rechte lijn q(x) boven p(x) en accepteer punten onder p(x)

=> Hoe hoger in dimensies je gaat hoe meer steekproeven er niet geaccepteerd zullen worden, en hoe moeilijk het wordt.
De kans dat een steekproef geaccepteerd wordt = Z/M. Dit betekent dat we gemiddeld M/Z pogingen nodig hebben tot een steekproef aanvaard wordt.

Hoogdimensionaal probleem:

• lage acceptatiegraad door

  • slechte match tussen q(x) en p(x)

  • constante M is te hoog ingesteld

• Oplossing

  • gebruik adaptieve rejection sampling: update q(x) tijdens het samplen

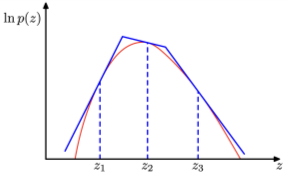
Voorbeeld: stuksgewijs q(x) lineair maken en telkens updaten om beter te matchen met de doeldistributie

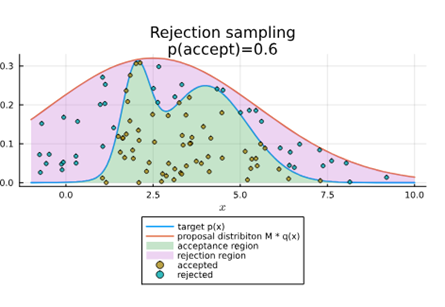
Teken een voorbeeldgrafiek van rejection sampling. Leid af hoe je van de acceptance probability gaat naar de acceptence rate. Leg de link met de oppervlaktes op je figuur.

Leg uit: de mixing time van een Markov chain.

Mixing time = de tijd die nodig is om de evenwicht stationaire distributie te bereiken.

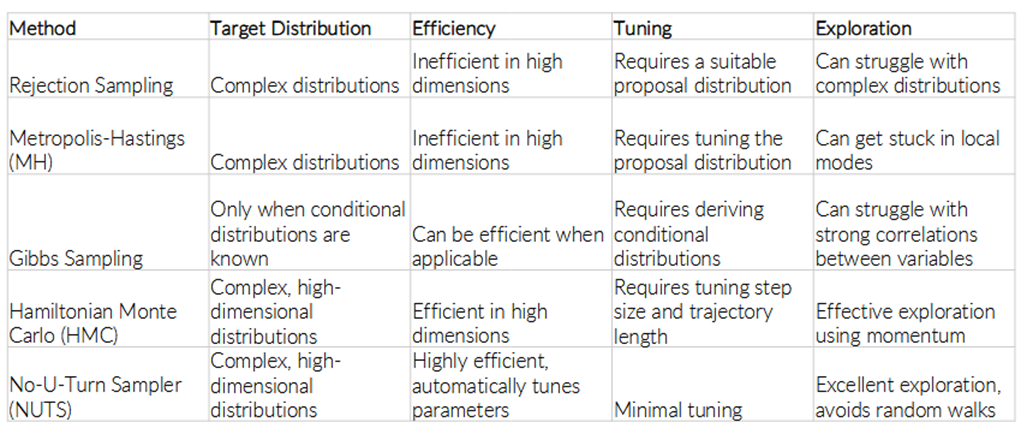
Wat zijn pseudosamples? Hoe bekom je die en wat is het verschil met gewone samples van een distributie?

Pseudosamples zijn kunstmatig gegenereerde data die niet echt gemeten zijn maar die je stimuleert uit een kansverdeling of model, samples van een keten (zijn afhankelijk)

Verschil met gewone samples

• Gewone samples zijn waarden uit de werkelijkheid

• Pseudo zijn gesimuleerde waarden uit een model

Hoe bekom je deze

• Gebruikt een random number generator een gespecifieerde verdeling

• Genereert getallen die lijken op de data

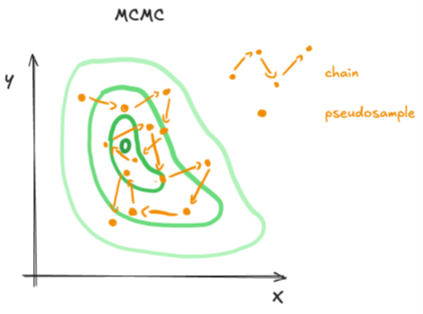
Leg in je eigen woorden het principe van Metropolis-Hastings sampling uit. Welk deel moet je zelf kiezen/ontwerpen voor je probleem?

Het Metropolis-Hastings-algoritme (MH)

• = ~= rejection sampling

• genereert pad waar elke nieuwe kandidaatsteekproef gebaseerd is om eerder geaccepteerde steekproef is vergelijkbaar met rejection samplin

Gebruiken weer een voorstelverdeling waaruit makkelijk kan bemonsterd worden

• Deze steekproeven kunnen weer geaccepteerd of afgewezen worden op basis van informatie uit de doelverdeling

• Is zo opgebouwd dat op lange termijn de waarschijnlijkheid om zich in een bepaald gebied te bevinden overeenkomt met de doeldichtheid of massafunctie

Procedure:

• Genereer een nieuwe kandidaatsample x* gebaseerd op de vorige sample x_t:

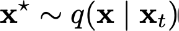
• Accepteer deze nieuwe sample met een kans:

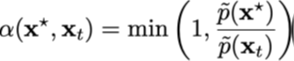
We hebben de neiging om de kandidaatsample te accepteren als deze naar regio's met een hogere dichtheid gaat

• Wanneer de acceptatiedistributie niet symmetrisch is, is de acceptatieprobabiliteit iets complexer

• Wanneer de sample geaccepteerd wordt stellen we dat  z(t+1) = z*. Anders wordt de sample verworpen en stellen we dat  z(t+1) = z(t)

Een enkele lange keten kan effectief zijn, aangezien er een bepaalde tijd nodig is voor de keten de doeldistributie volgt. Meerdere korte ketens zijn echter onafhankelijk en kunnen verschillende regio’s in de distributie verkennen.

Gegeven een grafiek van een distributie, leg uit waarom Metropolis-Hastings sampling al dan niet goed zal werken.

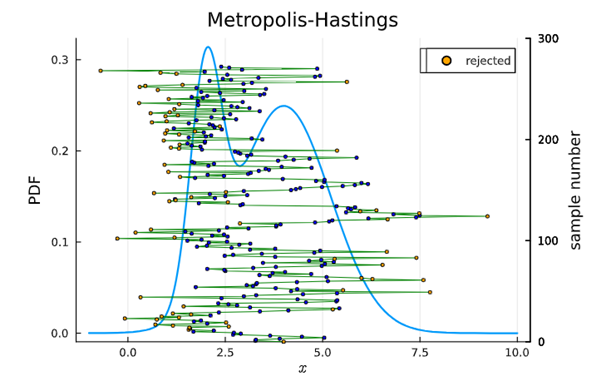
Werkt vooral goed als de verdeling smooth en unimodaal is

In dit geval

• Heeft minstens 2 duidelijke pieken: moeilijk met overspringen van ene piek naar de andere

• Lange tijd in 1 modus: keten blijft lang hangen rond de eerste piek en heeft moeite om naar de 2^e te gaan

• Veel voorstellen worden geweigerd -> inefficiënt samplen

 

Waarom werkt het?

De MH werkt omdat het een continu Markov-proces is, met transitiefunctie T(x(t+1),x(t)) , dat convergeert naar een stationaire distributie:

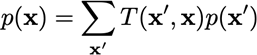
Onze acceptatieprobabiliteit zorgt voor een gedetailleerd evenwicht:

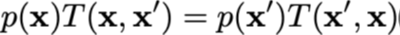
Als we kiezen dat T(x, x’) symmetrisch is, kunnen we de acceptatieprobabiliteit verkrijgen door een transitieprobabiliteit te kiezen:

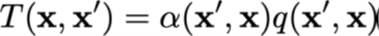
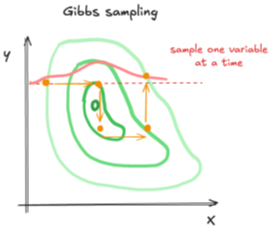
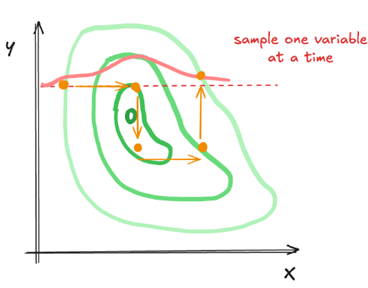
Leg in je eigen woorden Gibbs sampling uit.

Gibbs sampling is een speciaal geval van het MH algoritme, maar waarbij men 1 variabele per keer samplet, en de rest van de variabelen vast houdt.

Slimme manier om te samplen uit een complexe multidimensionele verdeling door steeds een variabele tegelijk te updaten terwijl je de rest vastzet

Wat is er bijzonder aan Hamiltonian Monte Carlo? Hoe verschilt de kwaliteit van de pseudosamples tegenover simpelere MCMC samplers? Wat zijn de nadelen?

Hamiltoniaans Monte Carlo is een type van MCMC die Hamiltoniaanse dynamieken gebruikt om efficiënte toestandstransities voor te stellen, wat toelaat de voorsteldistributie effectiever te verkennen dan traditionele random-walk-gebaseerde methoden.

Zetten de steekproefprobleem omzetten in een dynamisch systeem met behulp van ideeën uit de natuurkunde

Bij de vorige MCMC methoden kunnen we slechts relatief kleine stappen nemen. Ze zijn ook ‘blind’ → ze gebruiken weinig info over de distributie.

·        HMC gebruikt fysica om slim door de parameter-ruimte te bewegen, in plaats van te wandelen als een dronken man (zoals gewone MCMC dat doet).

Verschil

• Lange trajecten via fysische simulatie

• Heeft een bepaalde richting

• Acceptatie is groot

• Betere dekking van de ruimte

• Rekenkost is hoog per stap

Nadelen

• Moet gradiënten kunnen berekenen van de log posterior

• Elke stap vereist meerdere evaluaties

• Hyperparameters moeten goed gekozen worden, moeten geoptimaliseerd worden opdat HMC goed zou werken

  • Hiervoor gebruiken we NUTS(), hierdoor geen nood meer

  • HMC is computationeel duurder (meerdere integratiestappen per sample) dan de vorige methoden, maar een enkele stap kan veel verder reizen in de toestandsruimte

Bespreek de verschillen tussen twee gegeven MCMC sampling algoritmes.

Rejection sampling is geen MCMC

Gegeven visualisaties van de paden van verschillende sampling algoritmes, geef voor elk welk algoritme het heeft gegenereerd en leg kort uit hoe je dit kon herkennen.

1)

2)

3)

4)

5)

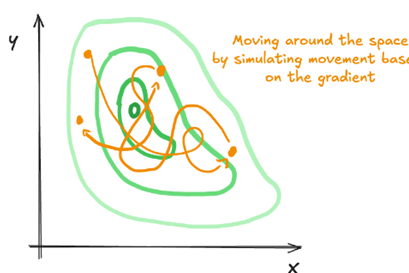
1) Rejection sampling: te herkennen doordat waarden niet geaccepteerd worden

2) Markov Chain Monte Carlo: Te herkennen door pseudosamples

3) Metropolis-Hastings: te herkennen dat voorstel distributie gecentreerd is rond vorige variabele

4) Gibbs sampling: te herkennen aan dat er maan 1 variabele per keer wordt gesampled

5) Hamiltonian Monte Carlo: Te herkennen aan elke stap is vrij ver van de andere → samples zijn van hoge kwaliteit

Wat is de "effective sample size" bij MCMC? Waarom is dit lager dan de lengte van je keten (aantal genomen samples)?

effective sample size

= aantal effectief onafhankelijke samples

= gecorrigeerd voor autocorrelatie

lengte van de keten bevat samples die dicht liggen en niet volledig onafhankelijk zijn

• Dit kan verschillen tussen de bulk (piek, mediaan, gemiddelde, …) en de staarten

Herken/beschrijf wanneer je MCMC zich goed gedraagt gegeven een diagnostische plot.

MCMC gedraagt zich goed wanneer de diagnotische plot eruit ziet als een harige rups.

Diagnostische plots:

·        We hebben fluctuaties rond een gemiddelde

·        We willen geen trends

Wat is een mogelijke oorzaak van een zich slecht-gedragende keten in MCMC? Hoe kan je dit oplossen?

Wanneer de keten niet convergeert: ligt het probleem vaak bij het model

Wanneer een model de data goed beschrijft, is er ideaal gezien één enkele piek die overeen komt met de optimale parameterconfiguraties

Je kunt de keten verbeteren door (zwak) informatieve priors te gebruiken

Geef het principe van de Monte Carlo methode. Leg uit hoe je Monte Carlo kan gebruiken om numerieke problemen op te lossen (integraal uitrekenen, probabiliteiten schatten). Bespreek voor en nadelen tov andere (deterministische) numerieke methodes.

De Monte Carlo-methode (= sampling methodes) verwijst naar een verzameling technieken waarbij willekeurige steekproeven worden gebruikt om complexe wiskundige of statistische problemen op te lossen. Deze methode wordt vaak toegepast wanneer een probleem analytisch moeilijk of onmogelijk op te lossen is (bv een hoge orde integraal).  

De algemene stappen van de Monte Carlo methode: 

• Willekeurig samplen van een parameterwaarde θ ~ P(θ)

• Uitvoeren van een simulatie gebruik makend van het model

  • Bv door een waarde van X te genereren volgens de verdeling P(X | θ). 

  • Stap 1 en 2 vele malen herhalen om een statistisch representatieve steekproef te bekomen

  • Hoe groter het aantal simulaties, hoe nauwkeuriger de resultaten

• Alle simulaties combineren voor statistische analyse

  • Om een schatting te maken via een statistische analyse

  • (bv je wil de grootheid gemiddelde schatten) 

Voorbeelden van toepassingen: 

• Numerieke integratie: In plaats van een ingewikkelde integraal exact uit te rekenen, simuleer je veel punten en bereken je hoeveel punten binnen het oppervlak liggen om een zicht te krijgen op de oppervlakte onder de functie. 

• Kansschattingen: Bijvoorbeeld: wat is de kans dat een systeem faalt binnen 10 jaar? Je simuleert duizenden scenario’s en telt hoe vaak het systeem binnen die tijd faalt. 

Voordelen: 

• Eenvoudig te implementeren 

• Breed toepasbaar: werkt ook voor zeer complexe of niet-lineaire modellen, en voor problemen in hoge dimensies. 

• Paralleliseerbaar: simulaties kunnen onafhankelijk van elkaar worden uitgevoerd, wat computationele efficiëntie oplevert bij gebruik van meerdere processors of computers. 

Nadelen: 

• Traag convergerend: om een goede schatting te maken, zijn vaak veel simulaties nodig.  

• Geen exacte oplossing: de uitkomst is altijd een benadering, met een zekere graad van onzekerheid. 

Deterministische methoden zijn vaak efficiënter: voor sommige goed-gedefinieerde problemen (zoals eenvoudige integralen) bieden klassieke methodes zoals de trapeziumregel of Simpsonregel snellere en nauwkeurigere resultaten.

De vergelijking voor de verwachtingswaarde van de functie van een toevalsveranderlijke is gekend als de Wet van de Onbewuste Statisticus. Geef deze en leg de link uit met MC.

E\left\lbrack g\left(x\right)\right\rbrack=\int_{-inf}^{+inf}g\left(x\right)f_{X}\left(x\right)dx

• Wet van de Onbewuste Statisticus  = verwachtingswaarde van een functie vd toevalsvariabele

• Als g(x) eenvoudig is zoals het oppervlak berekenen van een distributie van stralen X, kunnen we gebruik maken van een deterministische methode voor het berekenen van E[g(x)] (voorbeeld 24 p85).

• Maar als g(x) een moeilijke functie wordt (bv discontinu, niet-lineair of afhankelijk van een simulatiemodel) moeten we beroep doen op de MC methode:

1. Trek een groot aantal willekeurige steekproeven x₁, x₂, x₃, …, x_N uit de verdeling f_X(x)

2. Evalueer de functie g(x) op elk van deze steekproeven.

3. Bereken het steekproefgemiddelde als een benadering van de verwachtingswaarde:

E\left\lbrack g\left(x\right)\right\rbrack=\frac{1}{N}\cdot\sum_{i=1}^{N}g\left(x_{i}\right)

Gegeven een sample van X, leg uit hoe je P(A), E[X] en E[X|A] schat, waar A een event is.

P(A) → de kans dat gebeurtenis A zich voordoet

• Dit kan je berekenen door te berekenen voor hoeveel steekproevenwaarden A correct is & te delen door het totaal aantal steekproefwaarden

• (bv als A de gebeurtenis is ‘ X > 5 ‘, dan tel je hoeveel waarden groter zijn dan 5 en deel je dat door N)

E[X] → steekproefgemiddelde

E\left\lbrack X\right\rbrack=\frac{1}{N}\cdot\sum_{i=1}^{N}X_{i}

E[X | A] → steekproefgemiddelde conditioneel op A

• Dit is het gemiddelde van de waarden van X waarvoor A waar is (bv als A ‘ X > 5 ‘, dan neem je alleen die waarden waarvoor X > 5 en bereken je hun gemiddelde)

Wat is een “seed” in de context van random number generation? Waarom zou je die gebruiken/vastzetten?

In de context van random number generation wordt een "seed" gebruikt als startwaarde voor een algoritme dat willekeurige (pseudo-willekeurige) getallen genereert. Dit zijn pseudo-random getallen

·        Pseudo-willekeurige getallen zien eruit als willekeurig, maar eigenlijk zijn ze deterministisch berekend via een algoritme.

o   Ze kunnen echter perfect voorspeld worden als de startwaarde en het algoritme gekend zijn

o   De seed wordt in het begin gedefinieerd, zodat het resultaat exact gereproduceerd kan worden

·        Dus als je dezelfde seed gebruikt, krijg je altijd exact dezelfde reeks "willekeurige" getallen.

·        (Computers zijn deterministisch en kunnen geen echte ‘randomness’ genereren)

 

Waarom maken we gebruik van een seed?

·        Reproduceerbaarheid: in simulaties of statistische analyses is het belangrijk dat anderen (of jijzelf later) dezelfde resultaten kunnen bekomen. Een seed zorgt ervoor dat telkens dezelfde uitkomsten worden gegenereerd.

·        Testen en debugging: bij het ontwikkelen van code of modellen is het handig dat dezelfde pseudo-willekeurige invoer telkens opnieuw gebruikt wordt. Zo kan je foutopsporing doen zonder dat de resultaten elke keer anders zijn.

·        Vergelijkbaarheid: als je bijvoorbeeld twee modellen met elkaar vergelijkt, wil je dat ze dezelfde input krijgen om een eerlijke vergelijking te maken. Door dezelfde seed te gebruiken, werk je met identieke random data.

Wat zijn pseudorandom nummers? Welk algoritme wordt vaak gebruikt om deze te genereren?

Pseudorandom getallen zijn getallen die er willekeurig uitzien, maar eigenlijk het resultaat zijn van een algoritme. De getallen hebben geen statistisch herkenbare patronen, maar kunnen voorspeld worden als het algoritme & de startwaarde (seed) gekend zijn.

Eén van de meest gebruikte algoritmes is de Mersenne Twister. Dit algoritme genereert een getal sequentie gebaseerd op de Mersenne priemgetallen (≈ priemgetallen die kunnen herschreven worden als 2ⁿ – 1).

Hoe genereer je een observatie van X wanneer je de distributie f_X(x) kent en je random nummers in [0, 1] kan genereren?

Voor simpele distributies f_X(x) kunnen we gebruik maken van inverse transform sampling

·        Hierbij gebruikt men de inverse van de CDF F_X om het random getal U (uit het interval [0,1]) om te zetten naar F_X^-1(U)

o   We berekenen dus: X = F_X^-1(U)

·        Dit werkt omdat:

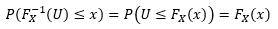
o   Dit toont aan dat de getransformeerde waarde X de juiste verdeling volgt

Er bestaan ook alternatieve methoden, bijvoorbeeld het Box-Muller transform voor wanneer f_X(x) de normale distributie is (en je wil een observatie uit een standaardnormale verdeling genereren)

·        Dit algoritme genereert twee standaard verdeelde waarden via twee random getallen U₁ en U₂ via:

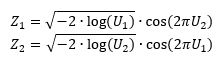
·        Achterliggend principe: de twee random getallen worden omgezet naar polaire coördinaten & vervolgens zetten we ze terug om naar het cartesische coördinatenstelsel. Deze laatste transformatie is zo gekozen dat de resulterende Z₁ en Z₂​ de verdeling van onafhankelijke standaardnormale variabelen benaderen.

 

Merk op dat de random getallen U₁ (en U₂) de pseudorandom getallen zijn die we bij vorige vraag hebben behandeld

Wat zijn quasi-random getallen? Waarvoor gebruik je ze? Welke eigenschappen hebben ze? Wat is een methode om ze te genereren?

Quasi-random getallen (= low-discrepancy sequences) zijn deterministische (≈ voorspelbare) getallenreeksen die speciaal ontworpen zijn om een ruimte zo gelijkmatig mogelijk te vullen.

·        Ze zijn deterministisch, maar hebben een lage discrepantie (= de maximale afwijking tussen het werkelijke aantal punten in een gebied en het verwachte aantal (voor een uniforme verdeling) is klein)

·        Niet bruikbaar als echte random getallen omdat ze te weinig toeval vertonen

·        Voor bepaalde toepassingen zijn pseudo-random getallen te random

→ gebruiken voor numerieke integratie, optimalisatie of voor MC simulaties waarbij uniformiteit belangrijk is.

Generatie gebeurt door de Sobol methode. (produceert zeer uniforme punten)

Vergelijking van de Mersenne Twister pseudorandom number generat  or & de Sobol methode:

→ wanneer je ze genereert in een [0,1] x [0,1] eenheidsoppervlak vullen quasi-random getallen de ruimte homogener dan pseudorandom getallen (minimalisatie van cluster/’groepjes’ vorming).

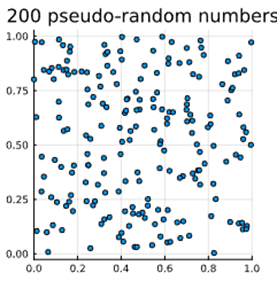
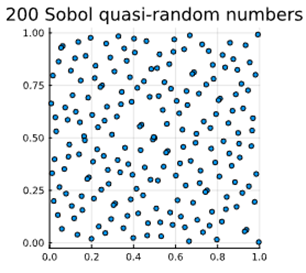
Wat zijn "true random numbers"? Waarom zou je die gebruiken? Hoe bekom je die? Wat is hun nadeel? Gebruik je die in huis, tuin en keukensimulaties?

True random numbers (echte willekeurige getallen) zijn getallen die voortkomen uit werkelijk onvoorspelbare, natuurlijke processen. Ze bevatten geen enkel algoritmisch patroon en zijn dus niet reproduceerbaar.

Deze kunnen alleen gegenereerd worden door een werkelijk stochastisch proces (bv iemand die een dobbelsteen gooit) of door een hardware random number generator. Dit soort generators zet bv elektrische ruis of kwantumfluctuaties om naar random getallen. Ze zijn dus erg duur om te genereren, waardoor ze ook niet heel toegankelijk zijn.

True random numbers zijn nodig in situaties waar volledige onvoorspelbaarheid cruciaal is, zoals: cryptografie (sleutels moeten volledig onvoorspelbaar zijn), online kansspelen / loterijen, casino software & experimentele fysica.

De nadelen zijn:

·        Ze zijn duur

·        Het duurt langer om ze te genereren dan pseudorandom numbers

·        Ze zijn niet altijd beschikbaar

·        Ze zijn niet reproduceerbaar

Bespreek de convergentie van het gemiddelde ifv. de steekproefgrootte en de implicatie voor Monte Carlo.

De variantie van het steekproefgemiddelde is:

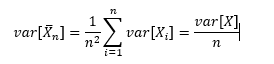
·        Hierbij zien we dat, voor eindige varianties, de variantie van het gemiddelde  omgekeerd evenredig is met de samplegrootte n.

·        Dit betekent dus ook dat de standaarddeviatie van het gemiddelde omgekeerd evenredig is met  sqrt(n) (herinner dat var = σ²):

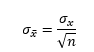
·        Dit betekent dat om de standaardfout 10x kleiner te maken, we de samplegrootte moeten vergroten met een factor 100.

De centrale limietstelling stelt dat, voor voldoende grote n, het steekproefgemiddelde ​  benaderend normaal verdeeld is, ongeacht de verdeling van de onderliggende data (zolang die eindige variantie heeft)

·        In praktijk wordt vaak aangenomen dat vanaf n ≈ 30 de normale benadering bruikbaar is

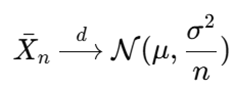
Monte Carlo methodes maken gebruik van steekproefgemiddelden om grootheden zoals integralen of verwachtingswaarden te benaderen. De bovenstaande eigenschappen hebben dus enkele belangrijke implicaties:

·        We kunnen de nauwkeurigheid vergroten, door meer samples toe te voegen

·        Door de CLT kunnen we foutmarges en betrouwbaarheidsintervallen inschatten

·      Trage convergentie: omdat de fout slechts daalt met 1/​, moet men exponentieel meer samples nemen voor lineaire winst in precisie

·        Deterministische methodes (zoals Gaussiaanse quadratuurregels) zijn vaak veel efficiënter bij lage dimensies of als de integrant voldoende glad is.

In onzekere of imperfecte modellen is extreme precisie vaak niet nodig; MC met beperkte samplegrootte geeft al een goed idee van de vorm en locatie van de uitkomstverdeling.

Bereken (ongeveer) het aantal observaties dat nodig is om een bepaalde precisie te bekomen met MC methode (gegeven de spreiding of initiële schatting).

De standaardfout van het gemiddelde is:

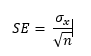
We willen nu dat SE < ε, met ε bepaalde door de gevraagde precisie. We krijgen:

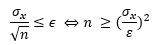
→ Als je weet dat σ_x = 2 en ε = 0.01, kan je berekenen dat je minstens 400 observaties nodig hebt

Bernouilli

= gebruikt in situaties waar twee uitkomsten mogelijk zijn

• Bv om de uitkomst van een muntstuk opgooien in te schatten (P(kop) = P(munt) = 0.5)

Binomiaal

= het aantal successen p in n aantal onafhankelijke pogingen simuleren

• Bv om het aantal keer munt in te schatten bij het 10x opgooien van een muntstuk

Geometrisch

= het aantal pogingen nodig tot een eerste succespoging

• Bv gebruikt om het aantal pogingen dat je nodig hebt om 6 te gooien met een dobbelsteen

Poisson

= tellen van het aantal gebeurtenissen in een tijds- of ruimte-interval, met een bekend gemiddeld aantal (λ) en onafhankelijke gebeurtenissen.

• Bv de hoeveelheid mensen die op een uur binnenkomen in een winkel

• Dit is een benadering van de binomiale distributie voor grote n & lage p → λ = n.p

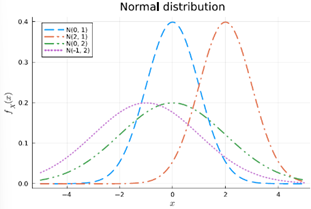
Normale verdeling

= continue variabele met natuurlijke variatie rond een gemiddelde (symmetrisch)

• Bv gebruikt voor de lichaamslengte van mensen

• Hierbij komen extreem grote mensen niet vaak voor

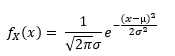
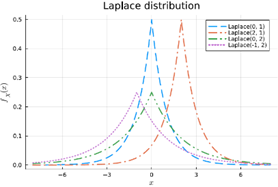
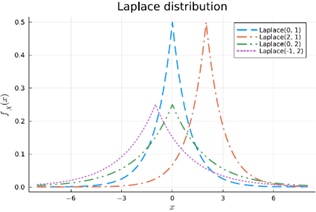
Laplace

= de normale distributie met dikkere staarten waardoor extremere events (grote mensen) vaker voorkomen

• Bv gebruikt voor financiële returns

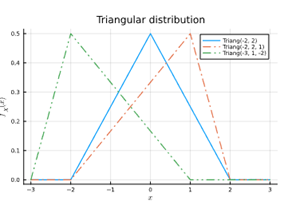
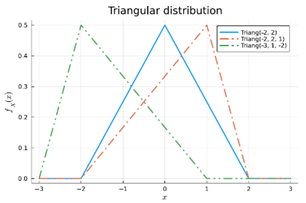
Triangulair

= gebruikt voor events met een duidelijke onder- en bovengrens & met een meest waarschijnlijke waarde (de top v/d driehoek)

• Bv bij projectmanagementschattingen ("optimistisch" als bovengrens, "realistisch" als top & "pessimistisch" als ondergrens)

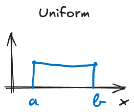
Uniform

= alle waarden in het interval [a,b] hebben dezelfde kans op voorkomen

• Bv de ogen van een dobbelsteen

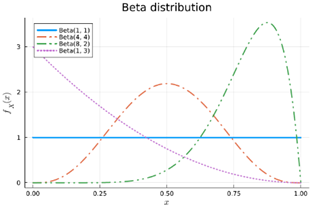
Beta

= verdeling over een succeskans van een Bernoulli, waarbij we kennis hebben over de voorbije α successen en β gemiste kansen

• Beta(4,2) → je hebt 6 keer geprobeerd & was 4 keer succesvol, drukt je geloof uit over de ware kans op succes (bv hoe goed je denkt dat je basketballen in de ring kan gooien)

• Hoe groter α & β, hoe meer zekerheid over de kans op succes

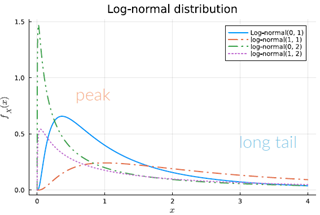
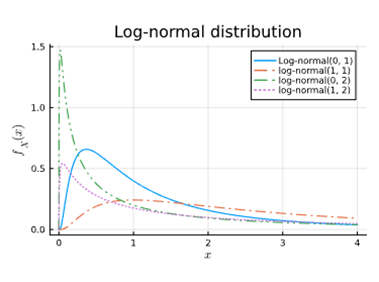
Log-normaal verdeling

= gebruikt voor een positieve variabele wiens logaritme normaal verdeeld is

• Bv gebruikt voor de grootte van stofdeeltjes te modelleren

• Veelgebruikt om biologische processen, zoals groeisnelheid, te modelleren

Exponentieel

= gebruikt om de tijd tussen twee gebeurtenissen te modelleren, met E[X] = 1/λ & λ de rate parameter

• Bv gebruikt om de tijd tussen twee celdelingen te modelleren

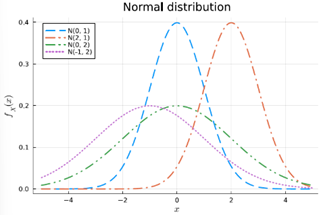
Bespreek de gelijkenissen en verschillen tussen de normale verdeling, de triangulaire distributie en de Laplace verdeling.

Gelijkenissen:

·        Symmetrisch rond een centrumwaarde

·        Eén piek (unimodaal)

·        Gebruikt voor schatting van continue variabelen

·        Gebruikt in simulaties

Aspect	Normale verdeling	Triangulaire verdeling	Laplace verdeling
Vorm	Klokvormig, glad (gausscurve)	Rechte lijnen – driehoek	Scherpere piek, dikkere staarten
Staarten	Dunne staarten – extreme waarden zeldzaam	Beperkte ondersteuning – geen extreme waarden buiten [a,b]	Dikke staarten – extreme waarden komen vaker voor
Gebruikelijke parameters	μ (gemiddelde), σ (standaardafwijking)	min, max, mode (top)	μ (locatie), b (schaal)
Realiteitsniveau	Gebaseerd op centrale limietstelling, zeer realistisch	Geschatte verdeling bij weinig data	Gebruikt als alternatief voor normaal bij outliers/extremen
Toepassing	Lichaamslengtes, IQ, fouten bij metingen	Projectplanning, eenvoudige expertinschattingen	Financiële returns, foutmodellen bij shocks

Geef drie distributies om een prior distributie op een kans (een getal tussen 0 en 1) te plakken.

Beta-distributie

• De meest gebruikte prior voor een kans

• Voorbeelden:

  • Beta(1,1) = uniforme prior (je weet niets)

  • Beta(4,2) = je verwacht eerder hoge kans op succes (vb. 4 successen, 2 failures in het verleden)

 Uniforme verdeling op [0,1]

• Eenvoudigste prior → stelt dat elke waarde tussen 0 en 1 even waarschijnlijk is. Geeft hierdoor ook wel gewicht aan onrealistische kansen (bv 0 of 1)

• Komt overeen met Beta(1,1).

 Triangulaire verdeling

• Gebruikt als je een ruwe schatting hebt van de meest waarschijnlijke kans, met bekende onder- en bovengrens.

• Voorbeeld: je denkt dat kans ≈ 0.7, maar kan liggen tussen 0.5 en 0.9 → gebruik triangulair(0.5, 0.7, 0.9).

Geef een distributie voor positieve reële getallen met een lange staart. Geef een voorbeeld van iets dat je kan voorstellen met deze distributie.

De log-normale distributie, deze kan gebruikt worden om de groeisnelheid van ontkiemende planten te modelleren.

Geef twee methoden om twee probabiliteitsdistributies te combineren in één complexere, gezamelijke (joint) PDF. Bespreek het verschil tussen de twee.

Eerste methode: het samenbrengen van onafhankelijke variabelen

·        De PDF wordt gevormd uit het product van de individuele variabelen:

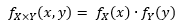
·        In Julia doen we dit via de Distributions library, met het command: product_distribution([dist1, dist2])

Tweede methode: Compounding probability distributions

·        De parameters van één distributie worden gezien als random variabelen & gemodelleerd via een andere distributie

·        In wiskundige notatie wordt dit:

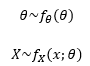
·        Dan wordt de gezamenlijke PDF:

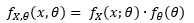
·        Deze methode wordt veel gebruikt in Bayesiaanse statistiek, omdat je onzekerheid over parameters kunt modelleren, en zo flexibelere modellen maakt.

·        In Julia wordt dit bijvoorbeeld:

 

De verschillen tussen de methodes:

Aspect	Onafhankelijke variabelen combineren	Compounding
Afhankelijkheid	Variabelen zijn onafhankelijk	Variabelen zijn afhankelijk via gedeelde parameters
Structuur	Simpel product van verdelingen	Hiërarchisch model, parameters zijn zelf random
Toepassing	Multivariate simulatie, vectoren van variabelen	Bayesiaanse inferentie, modelleren van onzekerheid

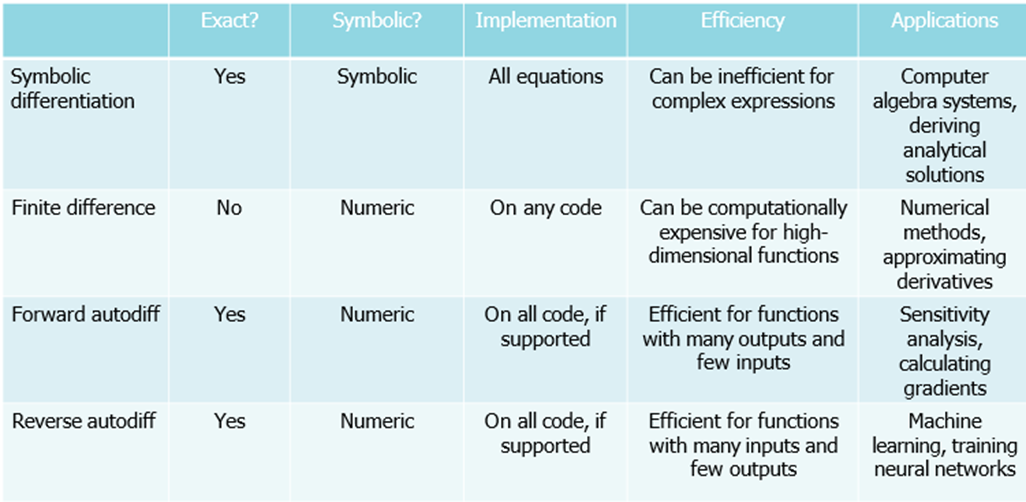
Leg de verschillende manieren uit hoe je afgeleiden met de computer kan bepalen, met hun voor- en nadelen.

Symbolische differentiatie met behulp van computeralgebrasystemen (zoals bv. Wolfram Alpha)

·        Symbolische differentiatie is een techniek die in de wiskunde en computeralgebra wordt gebruikt om de afgeleide van een functie symbolisch in plaats van numeriek te vinden.

·        Voordelen:

o   Geeft exacte afgeleiden, dit geeft direct inzicht in het gedrag van een systeem

o   Vaak is er zelfs een analytische oplossing

·        Nadelen:

o   Kan niet goed werken met bepaalde programmeerconcepten (for-loops, min/max…)

o   Resultaat is mogelijk niet numeriek stabiel

o   uitdrukking kan erg groot worden (“expression swell”): elke keer dat je afleidt krijg je een langere uitdrukking

Numerieke methoden: ipv. de limiet te nemen, neem je een klein stapje. Dit geeft een goede benadering

·        Eindige-differentiebenaderingen van de afgeleide of gradiënt zijn gebaseerd op directe functie-evaluaties. Ze benaderen de limietdefinitie van een afgeleide met eindige h:

    

o   We laten h niet naar nul gaan, maar naar een heel klein getal; dit is een goede benadering.

·        Fout op basis van de Taylor-reeks:
                  

·        Voordelen:

o   Vereist enkel dat we de functie kunnen evalueren op bepaalde punten, en werkt dus ook voor functies waarvan we geen formule hebben, zoals simulatiemodellen of experimentele meetdata

o   Dus het is eenvoudig te implementeren

o   Kan worden toegepast op black box!

o   Werkt voor elk type functie en code!

·        Nadelen:

o   Nauwkeurigheid kan laag zijn, inherent foutgevoelig

§  De nauwkeurigheid hangt af van de stapgrootte h:

·        Als h te groot is, missen we detail

·        Als h te klein wordt ontstaan er afrondingsfouten door het aftrekken van bijna-gelijke getallen

·        => Subtractieve annulatie en het leidt tot grote numerieke fouten

o   Vaak slechts eerste-orde nauwkeurig, tenzij je de centrale methode gebruikt, die tweede-orde nauwkeurig is. De fout in de voorwaartse methode is 0(h), terwijl de fout bij centrale benadering O(h²) is

o   Numeriek instabiel voor sommige functies

o   Alleen afleiding voor één invoer per keer, n-dim invoer = n evaluaties

Automatische differentiatie: door de computationele grafiek te manipuleren, je verandert je code zodanig dat die de afgeleide/gradiënt geeft

·        Automatische differentiatie (autodiff) is een set numerieke methoden die exacte afgeleiden of gradiënten geven door de computationele grafiek te manipuleren. Dit combineert het beste van de symbolische en numerieke differentiatie

·        Een computationele grafiek is een gerichte acyclische grafiek (geen lussen) die computercode weergeeft.

o   AD gebruikt de structuur van het computerprogramma

zelf om tijdens de uitvoering automatisch de kettingregel

toe te passen

o   Voorbeeld voor xy + 3:

·        Twee soorten:

o   Voorwaartse differentiatie (voor één-op-één of één-op-veel functies)

§  Vooral efficiënt als je weinig invoervariabelen hebt en meerdere uitgangen

o   Omgekeerde differentiatie (voor veel-op-één functies)

§  Ideaal als je veel inputs hebt en maar één output

·        Voordeel:

o   Je moet geen expliciete afgeleide op schrijven: je kunt gewoon je bestaande code gebruiken, en de afgeleide wordt automatisch en accuraat berekend, zelfs bij ingewikkelde functies met lussen, vertakkingen of het oplossen van differentiaalvergelijkingen

o   Exact, efficiënt en flexibel: combineert het beste van symbolische en numerieke differentiatie

o   Het berekenen van de afgeleide/gradiënt heeft dezelfde tijdscomplexiteit als een enkele functie-evaluatie!

o   Black box: geen formule voor de afgeleide

·        Nadeel

o   Je moet toegang hebben tot de broncode van de functie

o   Je moet vertrouwd zijn met de juiste tools. 

=> Samenvattend

·        Symbolische differentiatie ideaal is voor kleine, eenvoudige analytische functies

·        Numerieke differentiatie is eenvoudig en toepasbaar op simulaties maar minder accuraat

·        Automatische differentiatie combineert het beste van beide werelden, mits de juiste programmeeromgeving gebruikt wordt

De keuze van methode hangt dus sterk af van het soort functie, de beschikbaarheid van code, en de gewenste nauwkeurigheid. 

Gegeven de formule voor voorwaarde, centrale, achterwaarde, complexe stap, etc. numerieke differentie methode, leid de fout af a.d.h.v. een Taylor benadering.

De voorwaartse differentie is gebaseerd op twee functiewaarden:

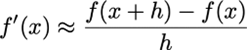
·        Foutenanalyse (via Taylor):

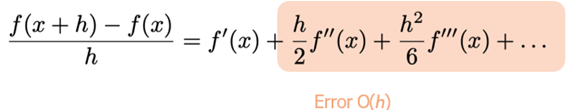
·        We verwerpen de 2^e en hogere-orde termen van de Taylorreeks. Als h klein is zal de eerste Taylor-term domineren, de andere zullen verwaarloosbaar zijn.

o   In Julia: dfs(f, x; h=1e-10) = (f(x+h)-f(x))/h

De centrale differentie is ook gebaseerd op twee functiewaarden:

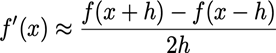
·        Foutenanalyse (via Taylor):

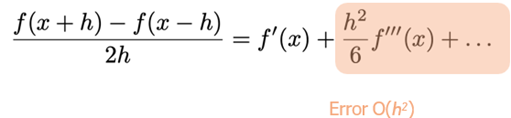
·        De tweede orde afgeleide valt weg, wat betekent dat de fout proportioneel is met het kwadraat van h → de fout is dan kleiner

o   In Julia: dcd(f, x; h=1e-10) = (f(x+h)-f(x-h))/2h

De complexe stapmethode is gebaseerd op de evaluatie van één enkele complexe functie:

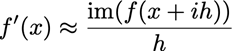
·        Foutenanalyse (via Taylor):

·        De oneven termen zijn reëel en de even termen zijn imaginair. Het imaginaire deel is een goede benadering van de afgeleide.

o   In Julia: dcs(f, x; h=1e-10) = imag(f(x+im*h))/h

Hoe kleiner de stapgrootte, hoe kleiner de hogere-orde termen van de Taylorreeks worden. Wanneer de termen te klein worden, hebben we numerieke problemen. Dit komt omdat reële getallen opgeslagen worden met slechts een eindige precisie.

Bij eindige differentiemethoden worden deze twee regels overschreden.

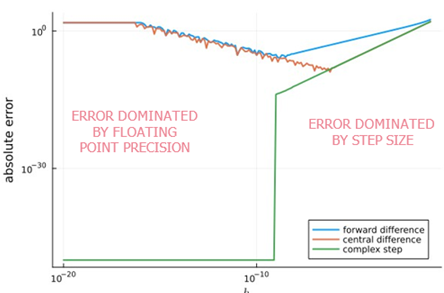
·        De misleidend goede nauwkeurigheid van de complexe stapmethode voor minuscule stapgroottes is te danken aan de eindige precisie floating point-getallen voor de functie-evaluatie zelf

·        Vanaf een bepaald punt stijgt de fout weer, omdat de fout kleiner wordt dan dat je accuraat kan voorstellen met floating points; je kan maar tot ongeveer 10^-8 gaan

Geef het numerieke probleem dat aan numeriek afleiden gebonden is en de twee belangrijke oorzaken (zondes) daarvan.

Numeriek differentiëren is een techniek waarbij de afgeleide van een functie f(x) benaderd wordt aan de hand van functiewaarden.

De eenvoudigste methode hiervoor is de voorwaartse verschilformule:

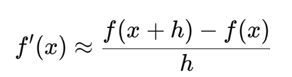
In theorie zou deze benadering nauwkeuriger worden naarmate de stapgrootte h kleiner wordt, omdat hogere-orde termen uit de Taylor-reeks dan verwaarloosbaar zijn. In de praktijk blijkt echter dat te kleine waarden van h tot numerieke problemen leiden, vooral op computers die gebruikmaken van eindige precisie (floating point getallen).

Het centrale numerieke probleem bij numeriek afleiden is dat het verschil f(x+h)−f(x) vaak heel klein is, en dat bij het uitvoeren van deze berekening precisie verloren gaat. Dit noemt men verlies van significantie. Het resultaat is dat de berekende afgeleide onnauwkeurig of zelfs volledig fout kan zijn.

Deze onnauwkeurigheid wordt grotendeels veroorzaakt door twee fundamentele fouten in numerieke analyse, ook wel de “twee zondes” genoemd:

1. Optellen van een klein getal bij een groot getal
   Wanneer een zeer klein getal wordt opgeteld bij een veel groter getal, gaat het kleinste getal verloren in de representatie. Zo zal bijvoorbeeld:

in een floating point systeem, omdat het verschil niet binnen de significante cijfers past. In het geval van numerieke afgeleiden kan dit leiden tot het compleet negeren van relevante informatie.

2. Aftrekken van bijna gelijke getallen
   Dit is het meest problematisch bij afgeleiden. Wanneer f(x+h) en f(x) bijna gelijk zijn (zoals bij een kleine h), levert hun verschil een getal op dat erg gevoelig is aan afrondingsfouten. Dit staat bekend als cancellation error, waarbij belangrijke significante cijfers verdwijnen. Daardoor kan het resultaat ernstig verstoord zijn of zelfs nul lijken, terwijl dat in werkelijkheid niet zo is.

Deze twee zondes zorgen ervoor dat numerieke afgeleiden onstabiel kunnen zijn en sterk afhankelijk zijn van de keuze van h. Een te grote stap leidt tot een grove benadering, terwijl een te kleine stap leidt tot numerieke onnauwkeurigheid.

Om dit probleem te vermijden, bestaan er betere methoden zoals:

·        Centrale verschillen, die een hogere nauwkeurigheid geven (foutorde O(h2)O(h^2) in plaats van O(h)O(h)).

·        Complexe stap methode, die gebruik maakt van een imaginaire stap ih in plaats van een reële, en zo geen subtractie vereist. Dit maakt de methode extreem nauwkeurig.

·        Automatische differentiatie, waarbij de afgeleide intern via de kettingregel op de code zelf wordt toegepast. Dit is snel, nauwkeurig en robuust, en vermijdt afrondingsproblemen.

Leg kort het verschil tussen voorwaards en achterwaards automatisch afleiden uit en wanneer je de ene of de andere zou gebruiken.

Voorwaartse differentiatie berekent de afgeleide van de input naar de output (cfr. kettingregel!)

·        We variëren slechts 1 parameter per keer; als de functie meerdere inputs heeft, moeten we voorwaartse accumulatie toepassen voor elke input

·        Vooral nuttig wanneer we meer outputs dan inputs hebben

·        We volgen dezelfde reeks bewerkingen als de oorspronkelijke code

·        Voorwaartse differentiatie kan worden geïmplementeerd met behulp van nilpotente getallen:

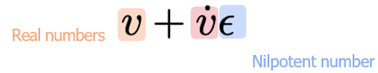
Dit is een ‘dual number’

De berekening is vergelijkbaar met complexe getallen:

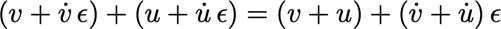
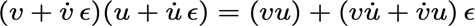
Functies evalueren via een Taylorreeks:

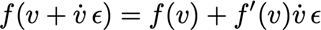
Dit is exact gelijk (dus niet slechts een benadering)

 

o   In Julia gebruiken we ForwardDiff: bv. ForwardDiff.derivative, ForwardDiff.gradient en ForwardDiff.hessian

Omgekeerde differentiatie berekent de afgeleide van de output naar de input (cfr. omgekeerde kettingregel!)

·        Eerst wordt de afgeleide van de output ten opzichte van zichzelf op 1 gezet

·        Vervolgens worden de afgeleiden van eerdere berekeningen stap voor stap teruggevoerd met behulp van de kettingregel. Dit proces gaat door totdat alle inputvariabelen hun afgeleide hebben

·        Resultaat: wijziging van de output t.o.v. alle inputgegevens wordt in één keer berekend!

·        Het is vooral efficiënt wanneer er één output is en veel inputs

·        In Julia gebruiken we Zygote

Wanneer welke?

·        Voorwaartse differentiatie: wanneer we meer outputs dan inputs hebben

·        Omgekeerde differentiatie: wanneer er één output is en veel inputs

 

Wat zijn stijve (stiff) differentiaalvergelijkingen? Wanneer zou je die tegenkomen? Wat is het probleem? Hoe ga je hier mee om?

= als de dynamiek van de oplossing op ten minste twee zeer verschillende tijdschalen reageert. (Sommige processen veranderen heel snel, terwijl andere veel trager verlopen.)

Voorbeeld:

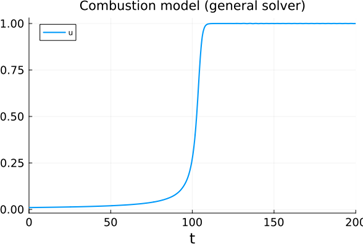
• We beschouwen een simpel verbrandingsmodel:

  • Een klein vuurballetje groeit proportioneel met zijn oppervlak en het gebruikt zuurstof proportioneel met zijn volume

• De evolutie van de straal u(t) kan beschreven worden met volgende DV:

u’ = u² – u³

• Als je geen solver gebruikt die dient voor stijve differentiaalvergelijkingen, krijg je een oscillatie op de oplossing: als je dicht bij 1 zit zullen de twee elkaar net wel of net niet opheffen

Waar komt dit voor?

• Biochemie: snelle reacties gecombineerd met tragere processen (bijv. enzymactiviteit vs. celgroei)

• Ecologie: snelle interacties (bv. predatie) naast trage groei

• Chemie: radicale reacties of reacties met zeer grote of kleine snelheidsconstanten

• Fysica: warmteoverdracht met grote temperatuursverschillen

Wat is het probleem?

Expliete methodes zoals Euler of Runge-Kutta zijn numeriek instabiel voor stijve systemen — ze vereisen extreem kleine tijdstappen om betrouwbaar te blijven. Dit maakt ze traag of zelfs onbruikbaar.

Bijv. als één component binnen milliseconden verandert en een andere over uren, dan moet je met expliete methodes die hele uren ook in milliseconden simuleren...

Hoe los je dit op?

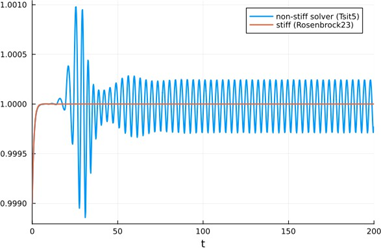
Gebruik een impliciete methode die wél stabiel is bij grotere stapgroottes:

• Rosenbrock-methodes: zoals Rosenbrock23() in Julia

• BDF-methodes (Backward Differentiation Formula): goed voor stijve problemen met gladde oplossingen

• Stiff ODE solvers in Julia, Matlab, Python etc.

Wat is het verschil tussen een expliete en impliciete numerieke methode om DVGn op te lossen? Herken of een methode expliciet/impliciet is.

Expliciete methoden berekenen y(t_n+1) direct uit y(t_n)

·        Voorbeeld: Forward Euler y(t_n+1) = y_n + ∆t f(t_n, y_n)

·        Makkelijk te implementeren, maar niet stabiel!

Impliciete methoden: volgende stap is afhankelijk van de huidige en toekomstige stap

·        Voorbeeld: Backward Euler y(t_n+1) = y_n + ∆t f(t_n+1, y_n+1)

·        Vereiste numerieke methoden (bijv. Newton-Raphson) voor elke stap, veel complexer en veeleisender

·        Impliciete methoden zijn veel stabieler en kunnen (beter) omgaan met stijve vergelijkingen

Wat is het verschil tussen "continuous" en "discrete callbacks"? Geef een mogelijke toepassing van elk.

Uit samenvatting:

·        Bij bepaalde reële systemen zal plotseling een parameter of variabele veranderen op een tijdstip of voorwaarde

·        Kan worden geïmplementeerd in het model, maar er wordt beter mee omgegaan door de solver om voldoende evaluaties rond de verandering te garanderen

o   We implementeren dit als callbacks in de solver

·        Twee typen callbacks in DifferentialEquations.jl

o   Continue callbacks: gebeurtenissen worden geactiveerd door specifieke gebeurtenissen (g(y)=0))

o   Discrete callbacks: gebeurtenissen worden geactiveerd op specifieke tijdstippen of na een specifiek aantal stappen

Wanneer we een systeem van differentiaalvergelijkingen simuleren, kunnen zich gebeurtenissen voordoen die plots veranderingen veroorzaken in de toestand of parameters van het systeem. In Julia (met het DifferentialEquations.jl ecosysteem) kunnen we zulke gebeurtenissen flexibel modelleren via callbacks. Er bestaan twee belangrijke types:

Continuous Callbacks (continue callbacks)

·        Wordt getriggerd zodra een voorwaarde door nul gaat tijdens de integratie.

·        De solver controleert continu of een bepaalde toestand of functie van toestanden nul wordt, en grijpt dan in.

Toepassing: een bal die valt en de grond raakt. Wanneer de hoogte h(t) nul wordt, moet de snelheid worden aangepast (bijvoorbeeld omgekeerd bij een botsing). Hier detecteert een continuous callback het moment waarop h(t)=0.

Discrete Callbacks (discrete callbacks)

·        Wordt uitgevoerd op bepaalde tijdstippen of bij specifieke stappen (niet continu gecontroleerd).

·        Dit is nuttig voor periodieke ingrepen of geplande acties.

Toepassing: een bioreactor waarin om de 6 uur een nieuwe dosis glucose wordt toegevoegd. Op vaste tijdstippen wordt dan de hoeveelheid substraat in het systeem verhoogd via een discrete callback.

Callbacks zijn zeer hulpzaam voor het controleren van problemen, dus dat is het gebruiken van external inputs voor het systeem om het gewenste gedrag te verkrijgen. 

Is het beter om plotse wijzigingen van input/parameters in je ODE systeem te incorporeren of via een callback af te handelen? Waarom?

Hoewel het technisch mogelijk is om plotse wijzigingen (zoals een abrupte verandering in een input of parameter) rechtstreeks in het differentiaalvergelijkingsmodel te verwerken, is het veel beter om hiervoor callbacks te gebruiken. Dit heeft verschillende voordelen:

Waarom callbacks gebruiken?

1.        Numerieke nauwkeurigheid: de solver weet exact wanneer een gebeurtenis gebeurt (bijv. wanneer een toestand een bepaalde drempel overschrijdt), en kan daar heel precies op inspelen.

2.        Efficiëntie: callbacks vermijden onnodig kleine tijdstappen die zouden ontstaan bij abrupte discontinuïteiten binnen het model zelf.

3.        Duidelijkheid en modulariteit: callbacks houden de ODE-formulering overzichtelijk en splitsen de modellogica van de simulatielogica.

4.        Robuustheid: callbacks worden ondersteund door gespecialiseerde algoritmen die automatisch de tijdstap aanpassen rond het event, wat fouten voorkomt.

Leg in je eigen woorden uit wat een Wiener process is. Welk fysisch proces modelleert dit? Is dit een "gladde" (smooth) functie?

Wiener process:

·        Een Wiener proces, ook wel een Brownse beweging genoemd, is een wiskundig model dat een willekeurige beweging beschrijft die door de tijd heen verloopt. Het is een soort "willekeurige wandeling" waarbij de volgende stap die je zet volledig toevallig is, maar toch aan bepaalde regels voldoet.

·        => Brownse beweging is de willekeurige beweging van deeltjes in een vloeistof. Het wordt veroorzaakt door botsingen tussen de deeltjes en de moleculen van de vloeistof

·        Het Wiener proces modelleert het fysische fenomeen van Brownse beweging

Brownse beweging kan worden gemodelleerd door het Wiener-proces W(t): dit is een stochastisch proces dat een stochastische variabele voorstelt in functie van de tijd

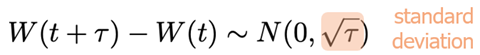
Dit model heeft dezelfde eigenschappen als een Markov keten

Intuïtief: voor elke kleine tijdstap τ voegen we een klein beetje Gaussische ruis toe. 

Het Wiener-proces is schaalvrij: als je een onderdeel van een grafiek neemt en inzoomt, ziet dit er exact hetzelfde uit. Dit wilt zeggen dat de functie niet afleidbaar is.

Voorbeelden: 

·        De beurs: waardes van aandelen evolueren volledig random

·        Beweging van dieren

·        Verspreiding van rook

"Gladde" (smooth) functie?

·        Nee !

·        Een Wiener proces is continu, maar niet differentieerbaar op welk tijdstip dan ook. Dat betekent dat de grafiek geen hobbels of sprongen heeft, maar dat hij zo grillig is dat je nergens een afgeleide kunt berekenen — hij is dus niet "glad". Het ziet er op een grafiek uit als een soort gekartelde, zenuwachtige lijn.

Geef de algemene vorm van een SDE. Wat moet je specifiëren? Wanneer zou je een SDE gebruiken?

Een stochastische differentiaalvergelijking (SDE) is een uitbreiding van een gewone differentiaalvergelijking (ODE), waarbij willekeurige ruis wordt toegevoegd om onzekerheid of variatie in het systeem te modelleren. De algemene vorm is:

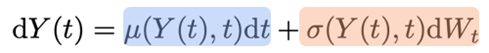
Waarbij:

·        een deterministisch deel (de driftcoëfficiënt),

·        Een ODE

·        Een stochastisch deel (de diffusiecoëfficiënt) aangestuurd door een Wiener-proces.

Nadat we een functie voor de trend (µ) en de ruis (σ) hebben bepaald, gebruiken we numerieke methoden om een ​​willekeurig traject te simuleren.

In Catalyst.jl is ruis standaard: elke reactie heeft ruis; de hoeveelheid ruis kan je schalen, maar de sterkte is proportioneel met de vierkantswortel van Y:

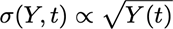
Ruis kan zorgen dat een bepaalde waarde onder nul gaat, die normaalgezien niet negatief kan worden (zoals bv. een concentratie).

Er wordt een willekeurig (stochastisch) proces toegevoegd om onzekerheid of variatie in het systeemgedrag te modelleren. SDE’s zijn vooral nuttig wanneer het gedrag van een systeem niet perfect voorspelbaar is, bijvoorbeeld door meetruis, fluctuaties op moleculair niveau of oncontroleerbare omgevingsinvloeden.

Wanneer gebruik je een SDE?

Je gebruikt een SDE wanneer het gedrag van een systeem:

·        Niet volledig deterministisch is (er is interne of externe ruis)

·        Gevoelig is aan toevallige fluctuaties

·        Willekeurige dynamiek vertoont, maar nog wel volgens bepaalde regels

Voorbeelden:

·        Populatiedynamiek met toevallige sterfte/geboorte

·        Biochemische systemen met lage aantallen moleculen

·        Weersvoorspellingen met onzekerheid

·        Financiële modellen, zoals aandelenprijzen of rentemodellen

Geef de algemene vorm van een SDE. Welk belangrijk stochastisch proces is hier relevant? Leg het uit in je eigen woorden.

Een stochastische differentiaalvergelijking (SDE) is een uitbreiding van een gewone differentiaalvergelijking (ODE), waarbij willekeurige ruis wordt toegevoegd om onzekerheid of variatie in het systeem te modelleren. De algemene vorm is:

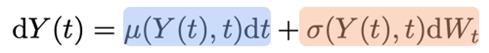
Waarbij:

• een deterministisch deel (de driftcoëfficiënt),

• Een ODE

• Een stochastisch deel (de diffusiecoëfficiënt) aangestuurd door een Wiener-proces.

Wat is het relevante stochastische proces?

Het Wiener-proces is hier cruciaal. Het zorgt voor de ruiscomponent in de vergelijking. In simulaties wordt dit benaderd met normaal verdeelde stappen met gemiddelde nul en standaardafwijking evenredig met sqrt(Δt)

Intuïtieve interpretatie:

Een SDE beschrijft systemen waarvan het gedrag zowel voorspelbare trends (zoals groei of afname) bevat, als toevallige schommelingen.

Vb: het modelleren van de populatie van een bacterie onder invloed van willekeurige omgevingsveranderingen.

Wat is een jump proces (cfr. het Gillespie algoritme)? Wat is het verschil met SDEs? Wanneer zou je een jump process gebruiken ipv een SDE?

Jump-proces

=stochastisch proces waarbij toestandsveranderingen optreden als plotselinge, discrete sprongen op willekeurige tijdstippen

Gillespie-algoritme

= discrete reactiesystemen te simuleren door iteratief de tijd tot een reactiegebeurtenis te simuleren.

• Algoritme modelleert de veranderingen in een systeem in de loop van de tijd door rekening te houden met individuele gebeurtenissen en hun waarschijnlijkheid → begrijpen hoe willekeurige fluctuaties het gedrag van het systeem beïnvloeden.

1. Initialiseer de systeemstatusvector x met de tellingen van alle soorten

2. Voor elke tijdstap, totdat t_end is bereikt:

   1. Genereer voor elke reactie de propensiteitsscore a_i(x)

   2. Bereken de totale propensiteit R=∑_ia_i(x)

   3. Neem een tijdstap τ ~ Exp(R)

   4. Kies willekeurig een reactie i die optreedt met een waarschijnlijkheid p_i=a_i(x)/R

   5. Update x volgens de stoichiometrie van de gekozen reactie i

   6. Update t = t + τ

Dit algoritme kan gelijktijdig omgaan met meerdere reacties.

Gillespie simulatie van het SIR model

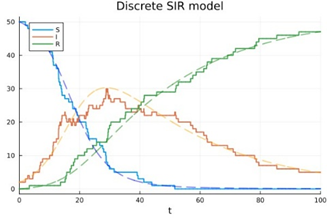
• De toestanden kunnen enkel afnemen of toenemen in stappen van 1

• Random fluctuaties kunnen de dynamieken beïnvloeden

We zien de Gillespie simulatie en de ODE oplossing op elkaar met dezelfde parameters.

Verschil met SDEs:

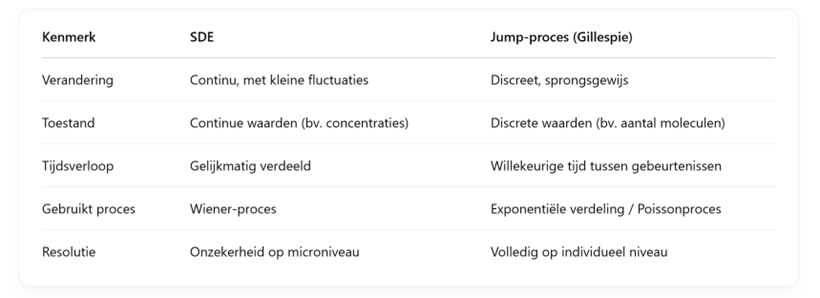
Wanneer kies je voor een jump-proces?

Je gebruikt een jump-proces (zoals het Gillespie-algoritme) wanneer:

·        Je systeem discrete aantallen bevat (zoals moleculen, individuen)

·        De getallen laag zijn, waardoor toeval een grote rol speelt

·        Je een exacte simulatie wil van de individuele gebeurtenissen (zoals reacties)

Bijvoorbeeld: een cel met 10 moleculen van een bepaald enzym – hier is een SDE ongeschikt, maar een jump-proces wel.

Gegeven een reactie met een kinetiek, geef de distributie en bereken de verwachte tijd tot een reactie-event adv de propensiteit.

Dit wordt in de cursus geïllustreerd met een voorbeeld: stel we hebben een systeem met n partikels dat doorheen de tijd vervalt met rate r via een eerste-orde proces. We kunnen deze reactie als volgt schrijven:

X\to O met reactiesnelheid r (o moet met een streep erdoor)

• De propensiteit op een tijdstip is nu:  (met n het overblijvende aantal deeltjes) Þ hoe meer deeltjes aanwezig zijn, hoe groter de kans dat er in een bepaald tijdsinterval een deeltje vervalt

Dit kunnen we aantonen via:

Deze kinetiek kunnen we nu omzetten naar een ODE:

x^{\prime}=-r\cdot x

Gegeven de initiële conditie x(0) = x₀ vinden we de distributie: 

x\left(t\right)=x_0\cdot e^{-rt}

De vervaltijd T van een partikel volgt dus een exponentiële distributie waarbij de verwachte tijd tot het verval van één partikel gelijk is aan: E[T] = 1/r

• We verwachten dus dat elk partikel minstens 1/r seconden overleeft

Via de CDF van de exponentiële distributie kunnen we de tijd tot verval berekenen:

P\left(T\ge t\right)=e^{-rt}

• Dus als we ons op tijdstip t bevinden, is de kans dat een partikel niet vervalt in een klein tijdsinterval τ gelijk aan:

partikel vervalt niet in :

P\left(\left\lbrack t,t+\tau\right\rbrack\right)=e^{-t\cdot\tau}

• Dit geldt slechts voor één partikel. Als we nu een systeem van n partikels beschouwen kunnen we de kans berekenen dat er geen verval reactie plaatsvindt in ons interval: 

geen enkel partikel vervalt in:

P\left(\left\lbrack t,t+\tau\right\rbrack\right)=\left(e^{-t\cdot\tau}\right)^{n}=e^{-r\cdot\tau\cdot n}

Zoals we zien volgt de kans dat één van de n partikels vervalt ook de exponentiële distributie, maar nu met een reactiesnelheid n*r  !

• Dit noemen de propensiteit van een reactie (= hoe geneigd een stof is om te reageren ≈ de kans per tijdseenheid dat een reactie zal plaatsvinden)

  • Een systeem met grote n heeft dus een grotere reactiesnelheid & er zal dus minder tijd zijn tussen de reacties

  • Een systeem met een snelle reactiesnelheid heeft een hoge propensiteit om daadwerkelijk plaats te vinden

  • De propensiteit & dus de reactiesnelheid van de exponentiële distributie verandert met het aantal overblijvende partikels, totdat het systeem geen partikels meer bevat

Systemen waarbij n oneindig is, hebben infinitesimale kleine tijdsintervallen tussen de opeenvolgende vervalreacties & kunnen dus benaderd worden als deterministisch & continu.

Leg in je eigen woorden het principe van het Gillespie algoritme uit.

Het Gillespie-algoritme kan worden gebruikt om discrete reactiesystemen te simuleren door iteratief de tijd tot een reactiegebeurtenis te simuleren.

Het Gillespie-algoritme is een methode om het gedrag van stochastische reactienetwerken exact te simuleren, met volledige weergave van het toeval in wanneer en welke reactie gebeurt.

Stap-voor-stap:

1. Initialiseer de systeemstatusvector x met de tellingen van alle soorten

2. Voor elke tijdstap, totdat t_end is bereikt:

   1. Genereer voor elke reactie de propensiteitsscore a_i(x)

   2. Bereken de totale propensiteit R=∑_ia_i(x)

   3. Neem een tijdstap τ ~ Exp(R)

   4. Kies willekeurig een reactie i die optreedt met een waarschijnlijkheid p_i=a_i(x)/R

   5. Update x volgens de stoichiometrie van de gekozen reactie i

   6. Update t = t + τ

Kenmerken:

·        Geen tijdsdiscretisatie nodig (zoals bij SDE's of ODE's)

·        Volgt exact de kanswetten (law of mass action op microschaal)

·        Toepasbaar bij lage molecule-aantallen waar toevallige fluctuaties belangrijk zijn

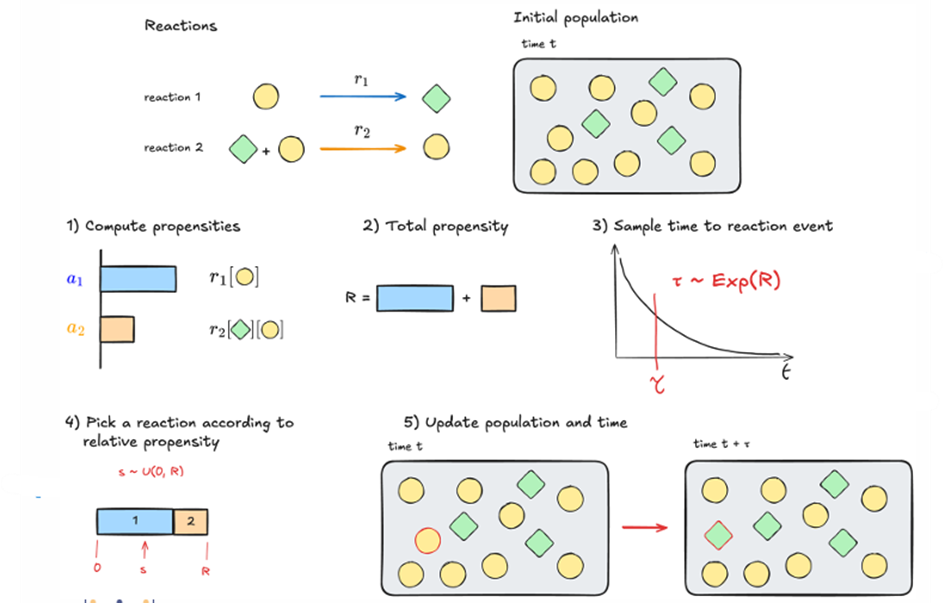
Ga van een simpele beschrijving van een systeem naar een massabalans en een stelsel van DVGn.

De toestand y of toestandsvector y stelt een fysische waarde voor van het systeem waarin we geïnteresseerd zijn. Met ODE’s (ordinary differential equations) kunnen we beschrijven hoe deze hoeveelheden veranderen in de tijd:

We kunnen modellen afleiden via het gebruik van behoudswetten:

·        Behoud van energie

·        Behoud van lading

·        Behoud van momentum

·        Behoud van massa

Change = input – output + production - consumption

Processen zijn vaak afhankelijk van toestanden of externe factoren (tijd).

Vervolgens stel je dit op als een differentiaalvergelijking (DVG): 

Wat is een conservatiewet? Pas de algemene formule voor conservatiewetten toe op een gegeven systeem.

Behoudswetten:

·        Behoud van energie

·        Behoud van lading

·        Behoud van momentum

·        Behoud van massa

·        Change = input – output + production – consumption

Een conservatiewet is een fundamenteel natuurkundig principe dat zegt dat bepaalde grootheden — zoals massa, energie of lading — niet zomaar ontstaan of verdwijnen. Ze kunnen enkel verplaatst worden of omgezet worden van de ene vorm naar de andere. 

In een biosysteem betekent dit meestal: 

·        Massa kan het systeem binnenkomen of verlaten (via in- en uitstroom), 

·        Of worden gevormd of afgebroken door processen (zoals reacties) 

Voor een eenvoudige massabalans: 

                       

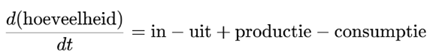
Voorbeeld: als er 10 kg water per uur in een tank stroomt en er 7 kg per uur uitgaat, stijgt de massa in de tank met 3 kg/u. 

Beschrijf de vijf stappen van massabalans modellering.

1.        Definieer systeemgrenzen

2.        Identificeer hoeveelheden die van belang zijn

3.        Formuleer balansvergelijkingen

4.        Druk de verschillende componenten wiskundig uit

5.        Verkrijg differentiaalvergelijkingen

Eens je het stelsel van ODEs hebt en de waarden van de parameters en beginwaarden kent, kun je het stelsel analytisch of numeriek oplossen.

Geef de wet van Massa-Actie Kinetiek. Leg uit hoe die intuïtief tot stand komt.

Voorafgaande info:

·        Wanneer het gaat over (bio)chemische systemen, die gekarakteriseerd worden door chemische vergelijkingen, beschouwt men reacties van de vorm:

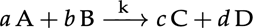
·        Deze reactie gaat door met een reactiesnelheid v:

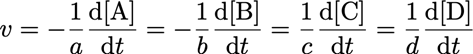
·        Deze reactiesnelheid zal meestal niet constant zijn, aangezien de concentraties van de reagentia veranderen doorheen de tijd.

Massa-actie kinetiek:

·        Een vaak gebruikt model voor het bepalen van de reactiesnelheid is de wet van massa-actie, die zegt dat de geneigdheid (=’propensity’) dat een reactie doorgaat proportioneel is aan de concentraties van de reagentia die moeten interageren:

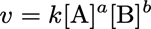
o   Hierbij is k de reactieconstante.

Intuïtief:

·        We kijken naar het systeem op een micro-level: binnen een infinitesimale tijdsperiode zal een reactie doorgaan als a moleculen van A en b moleculen van B botsen op juist die manier dat een reactie doorgaat. Deze kans op botsing is proportioneel met de concentraties van alle moleculen en met de reactiesnelheid v.

·        De Julia library Catalyst.jl biedt een intuïtieve interface om chemische (en gerelateerde) systemen te modelleren via een domeinspecifieke taal (DSL).

Leg het verschil uit tussen de reactieconstante en de reactiesnelheid.

De reactieconstante:

• Aangeduid met de letter k, is een vaste waarde die de intrinsieke snelheid van een reactie beschrijft onder bepaalde omstandigheden (zoals temperatuur, druk en aanwezigheid van katalysatoren). 

• Je kan het zien als een eigenschap van de reactie zelf. Hoe groter k, hoe sneller de reactie kan verlopen, als er voldoende reagentia zijn. 

  • k heeft verschillende eenheden, afhankelijk van de orde van de reactie (bijvoorbeeld s⁻¹, L/mol·s, ...). 

  • De waarde van k verandert niet tijdens de reactie, tenzij je de omstandigheden (bv. temperatuur) wijzigt. 

De reactiesnelheid:

• v is de werkelijke snelheid waarmee een reactie op een bepaald moment verloopt. Het geeft aan hoe snel de reagentia verdwijnen of de producten gevormd worden, en verandert in de tijd. 

• De reactiesnelheid wordt berekend op basis van: 

  • De reactieconstante k, 

  • De actuele concentraties van de reagerende stoffen, 

  • De vorm van de reactie (via de massa-actie wet)

Herken, geef voorbeelden van en beschrijf de kinetiek met DVG van: Nulde-orde processen

Voor processen van de nulde-orde is de kinetiek niet afhankelijk van de concentratie of dichtheid.

Hierbij hebben we een constante toevoeging aan (r > 0) of verwijdering uit (r < 0) het systeem.

Nulde-orde reacties kunnen in eender welk toepassingsdomein voorkomen:

·        Hydraulica: water met een constant debiet toevoegen of wegnemen

·        Chemie: een chemische verbinding wordt met constante snelheid toegevoegd aan een reactor

·        Biochemie: enzymatische reacties

In Catalyst.jl zijn processen nulde orde volgens default: r, 0 --> y
 Om specifiek mee te geven dat het over een nulde-orde proces gaat: r, y => 0

Bij constante verwijdering uit een systeem moeten we opletten, omdat deze toestanden geen negatieve waarden kunnen aannemen.

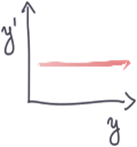
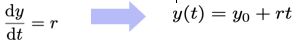
Herken, geef voorbeelden van en beschrijf de kinetiek met DVG van: eerste-orde processen

Voor processen van de eerste-orde is de reactiesnelheid evenredig met de waarde van y.
 

Hierbij hebben we exponentiële groei (r > 0) of afname (r < 0).

Voorbeelden:

·        Hydraulica: lekken van water, proportioneel met de druk aan de onderkant

·        Biochemie: groei van micro-organismen

·        Warmtesystemen: afkoeling volgens de wet van Newton (afkoeling is proportioneel met het temperatuursverschil)

Eerste-orde processen zijn vaak niet realistisch: exponentiële groei is nooit houdbaar vanwege beperkte draagkracht en exponentiele afname gaat slechts naar 0 in de limiet, wat onrealistisch is.

In Catalyst.jl:

·        Productie: r, y --> 2y

·        Afname: r, y --> 0

Herken, geef voorbeelden van en beschrijf de kinetiek met DVG van: tweede-orde processen

Voor processen van de tweede orde is de reactiesnelheid evenredig met het kwadraat van de  waarde van y.

→ kan oneindig bereiken in een eindige tijd! Dit is superexponentiële groei

Voorbeelden:

·        Chemie: decompositie van stikstofdioxide

·        Biochemie: DNA hybridisatie: hangt af van de concentratie van beide strengen

·        Ecologie: voortplanting, beide geslachten moeten aanwezig zijn

o   In ecologische systemen is de wet van massa-actie een benadering van zoekgedrag

Tweede-orde processen komen voor wanneer 2 soorten elkaar vinden en een interactie ondergaan. De kans op een ontmoeting is proportioneel met het product van de dichtheden van de interagerende soorten. Dit is slechts een benadering.

In Catalyst.jl:  r, A + A --> C;      r, A + B --> C