Math Finals Year 9

Mathematics

○

greater than/less than

●

greater than/less than or equal to

What happens when we multiply or divide both sides of an inequality by a negative number?

The inequality symbol is reversed

What happens if we swap the sides of an inequality?

The inequality symbol is reversed too

Substitution

Substitution can be used to solve simultaneous equations. It is used when at least one of the equations has a single variable as the subject. For example, y is the subject in the equation y = 3x + 1

Solving a simultaneous equation using substitution

1 Substitute one equation into the other, using brackets.

2 Solve for the remaining variable.

3 Substitute to find the value of the second variable.

Elimination method

when you add or subtract two equations to eliminate one of the variables, sometimes, this could require you to multiply or divide to create a matching pair

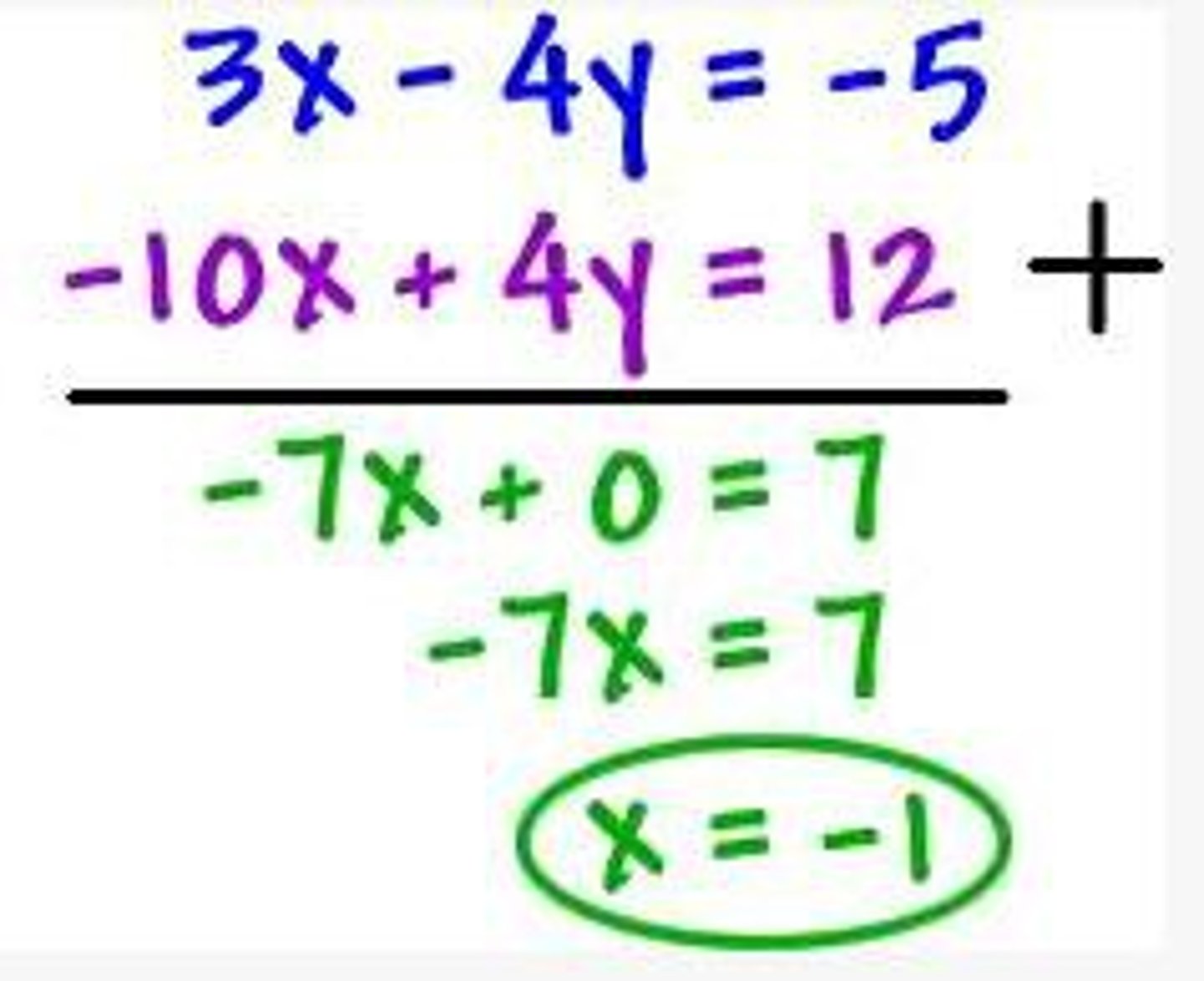
Add equations to...

Eliminate opposite signs

Subtract equations to...

Eliminate opposite signs

y=mx+c

y= y point

m= gradient

x= x point

c= y intercept

How to graph a straight line.

Two points are required to sketch a straight

line graph. Often these points are the axes

intercepts.

Gradient Formula

y2-y1/x2-x1

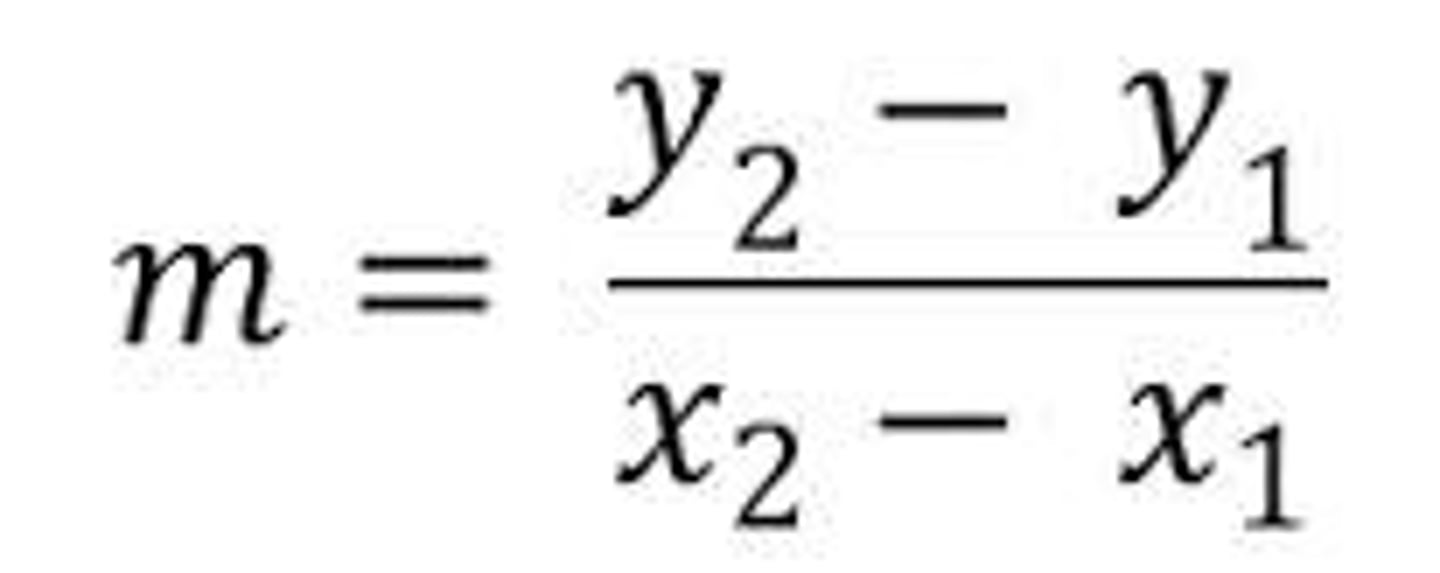
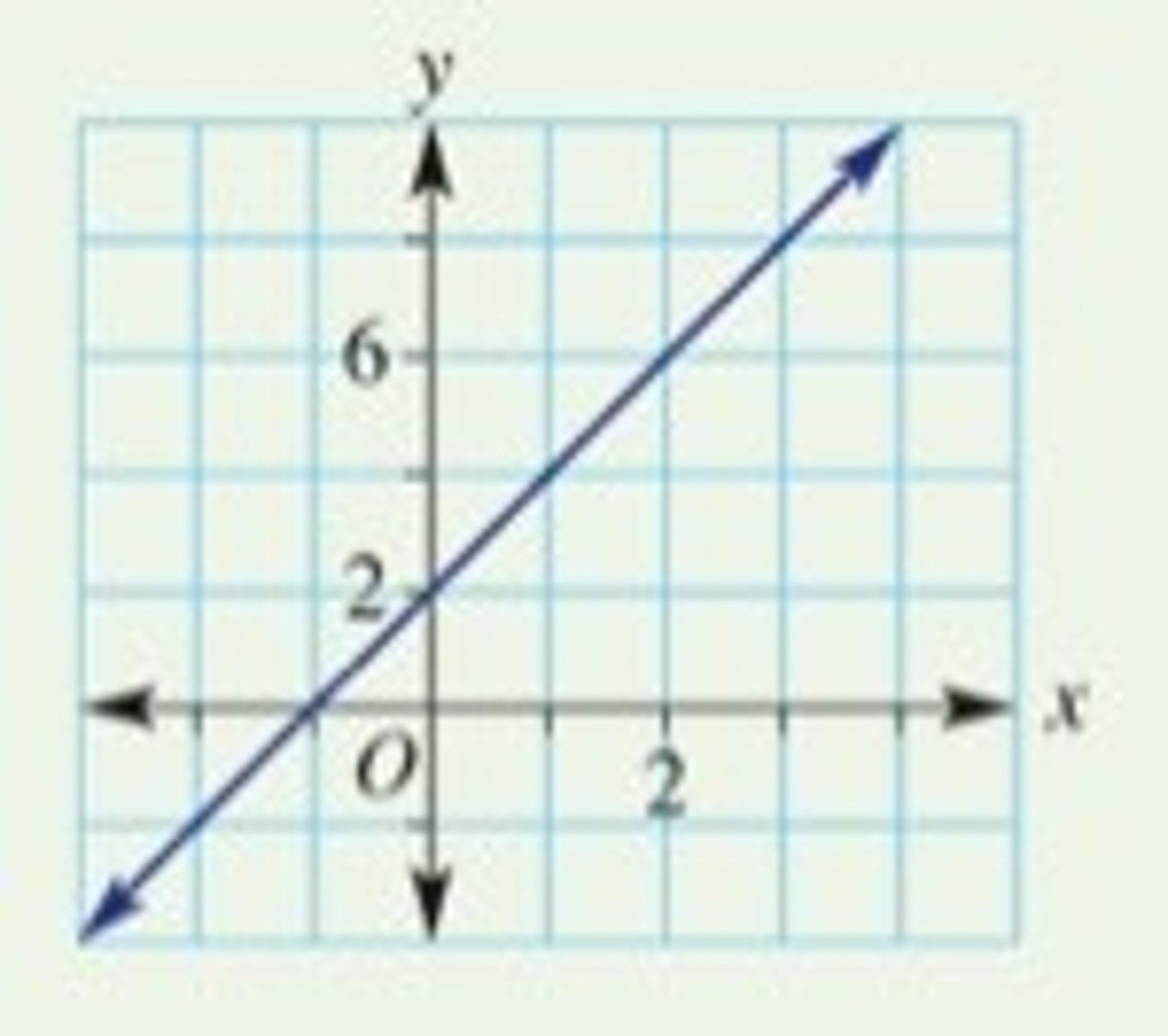
Positive Gradient

a line that goes up from left to right

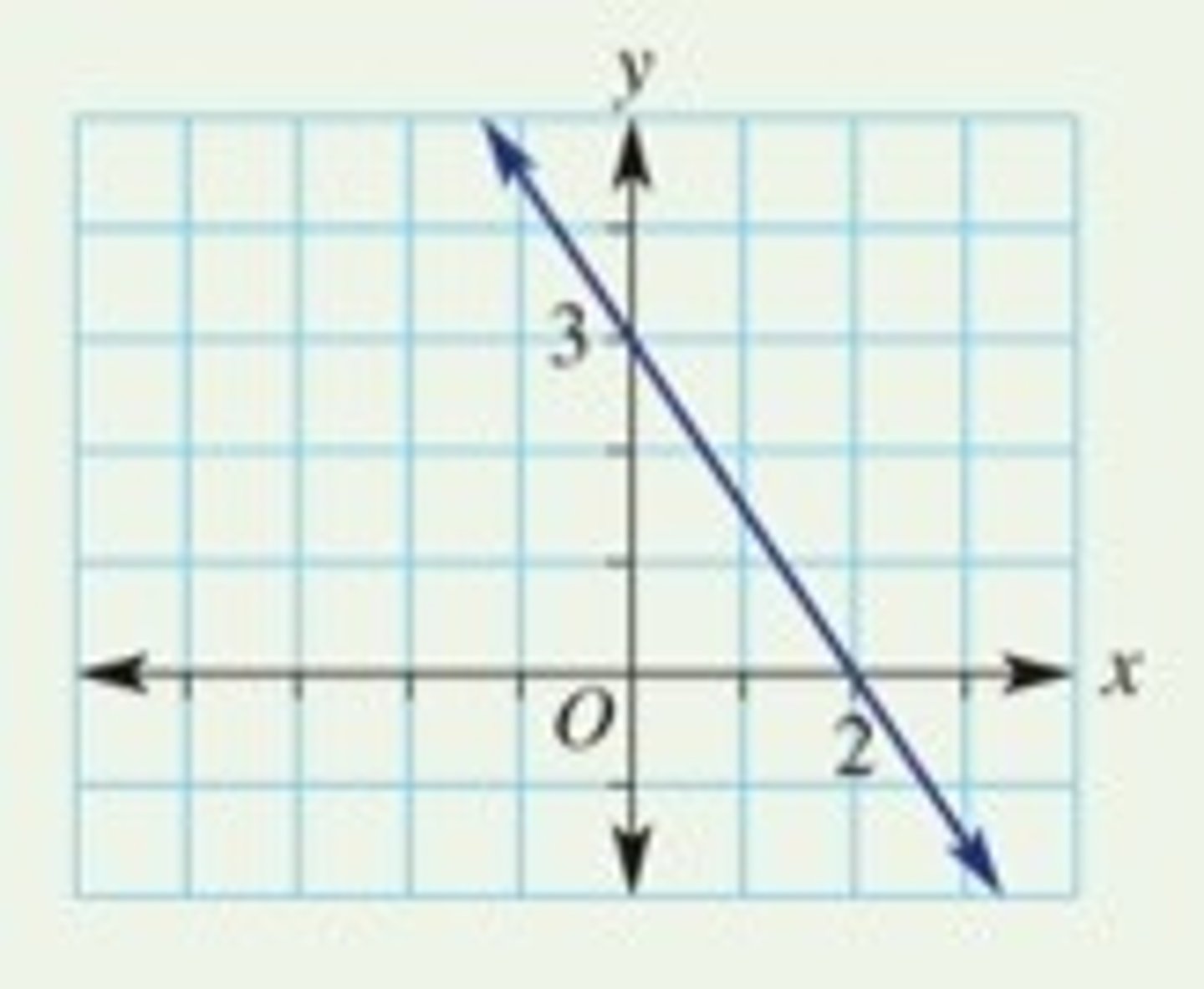
Negative Gradient

a line that goes down from left to right

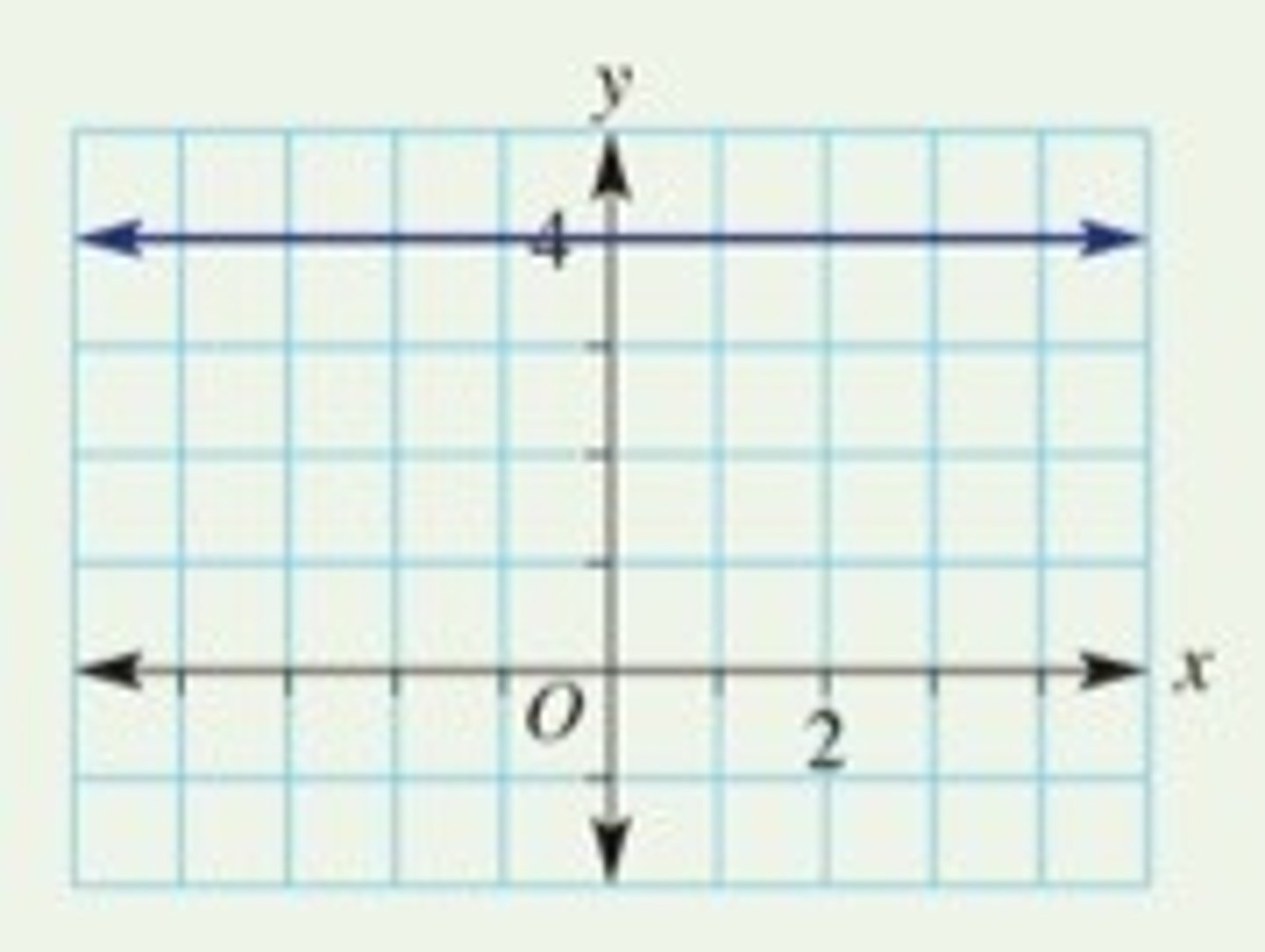
Zero Gradient

horizontal line

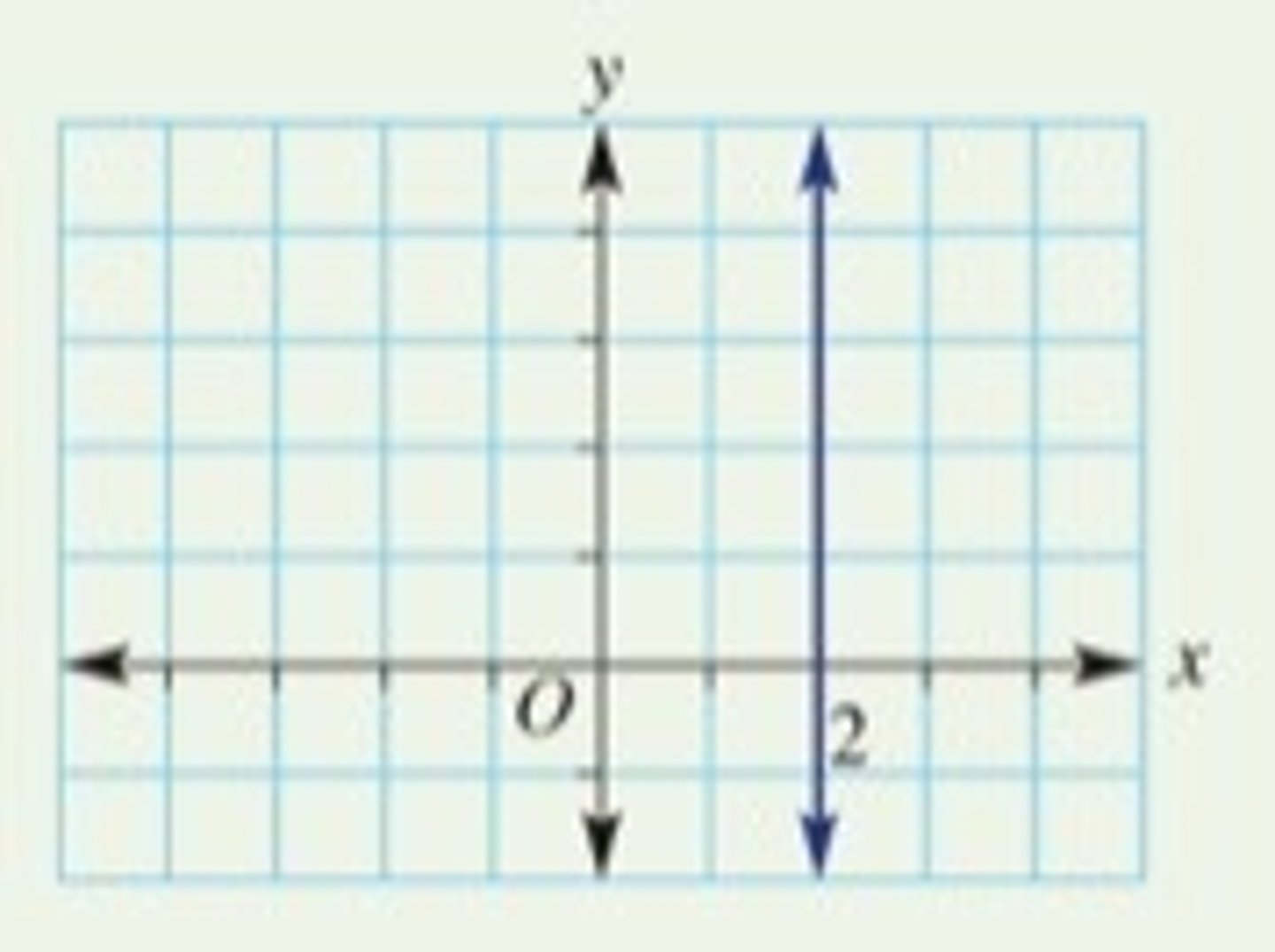
Undefined Gradient

a line that goes vertical

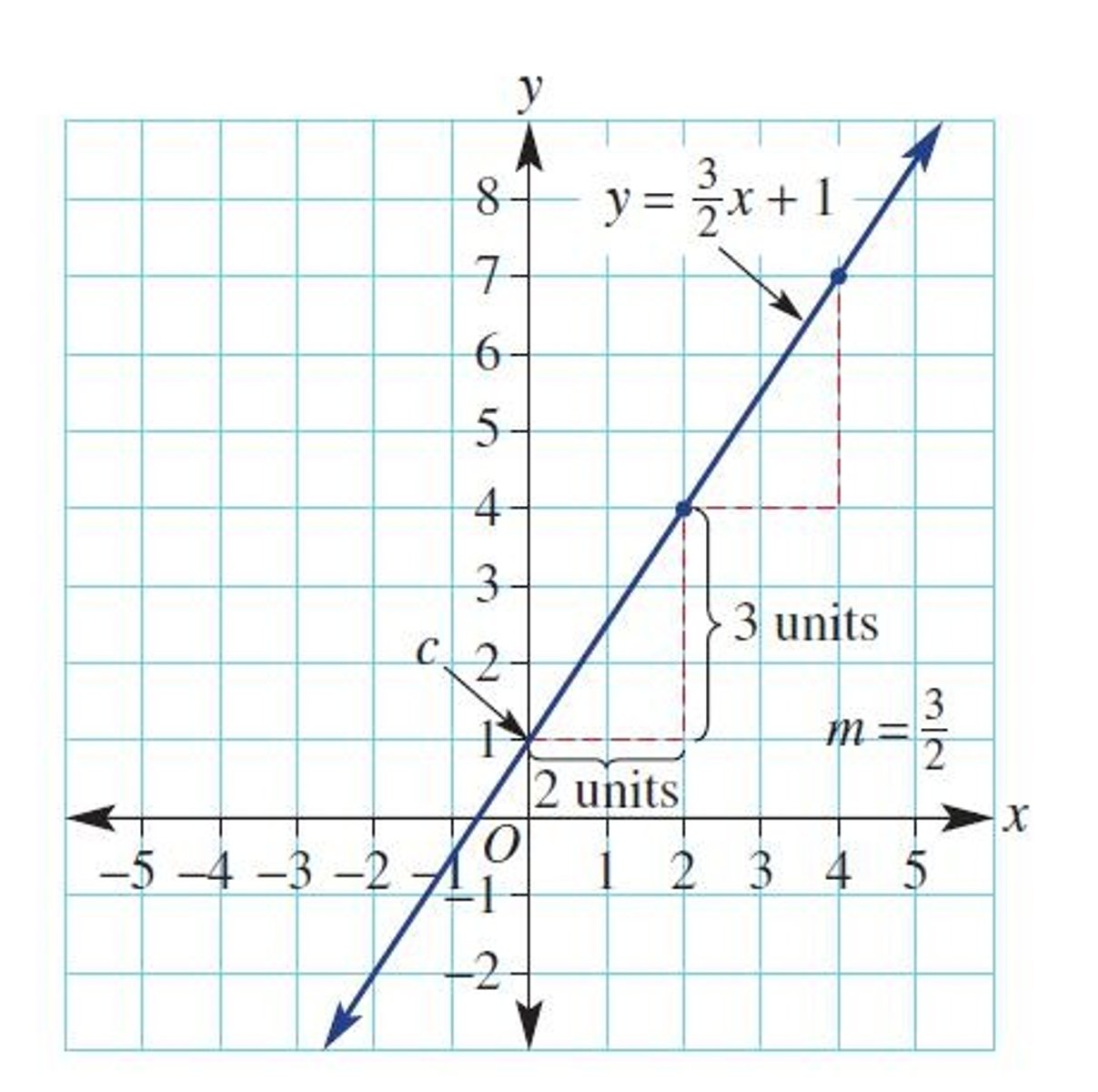
Gradient Intercept Form

To sketch a graph using the gradient-intercept method, locate

the y -intercept and use the gradient to find a second point.

Distance of a line segment formula

d = √((x₂ - x₁)² + (y₂ - y₁)²

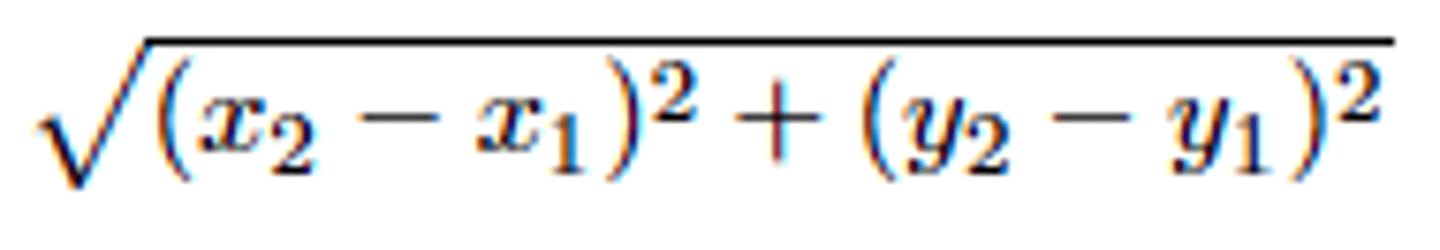
Complement

a probability of something not happening

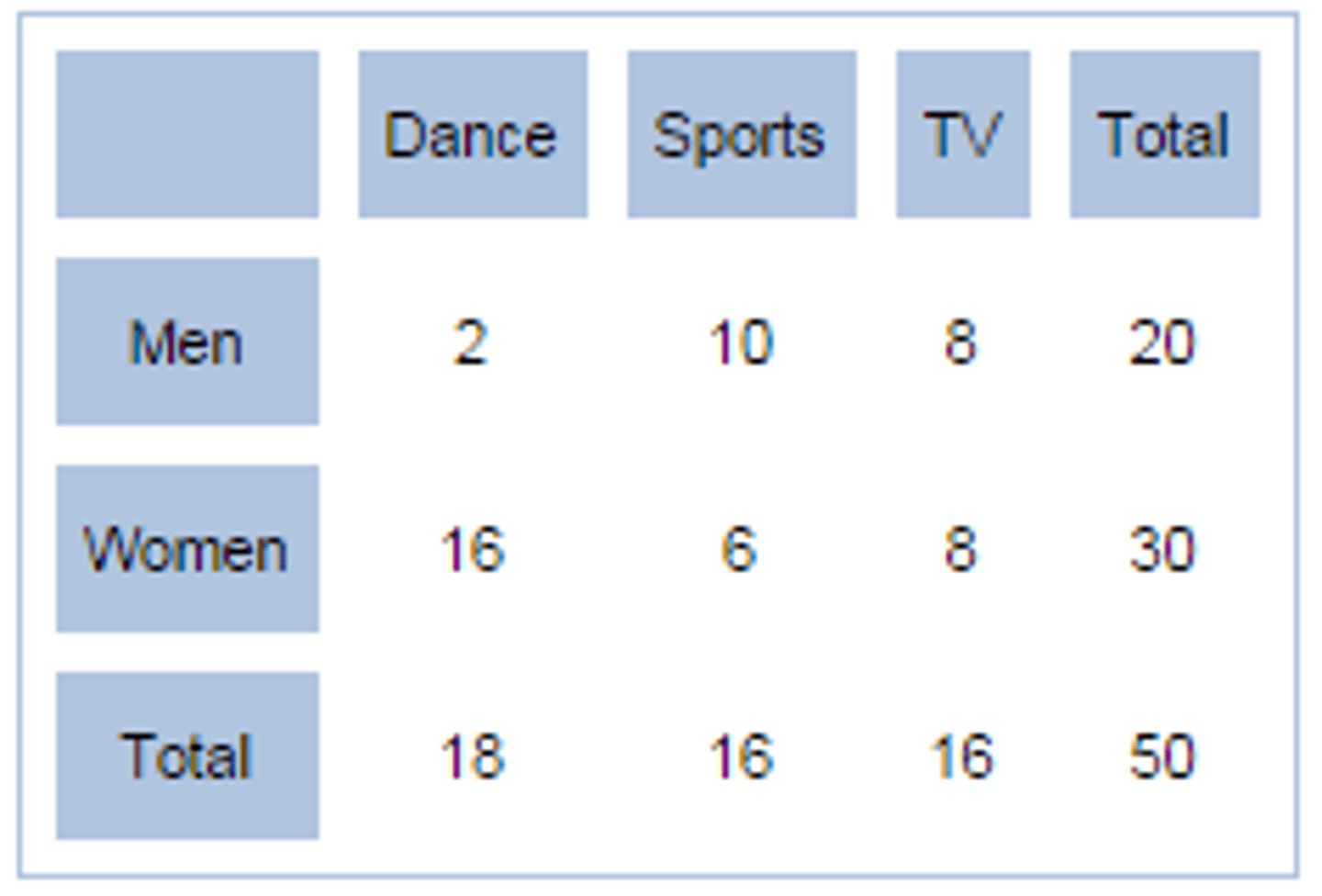
Two way tables

Describes two categorical values according to a row variable and a column variable.

Ω

Sample space

⊂

Subset. A particular part of a sample space

∈

an element of a set

∅

Empty set

n(A)

cardinal number

∪

Union, either A or B

∩

intersection - middle

A

only elements of A

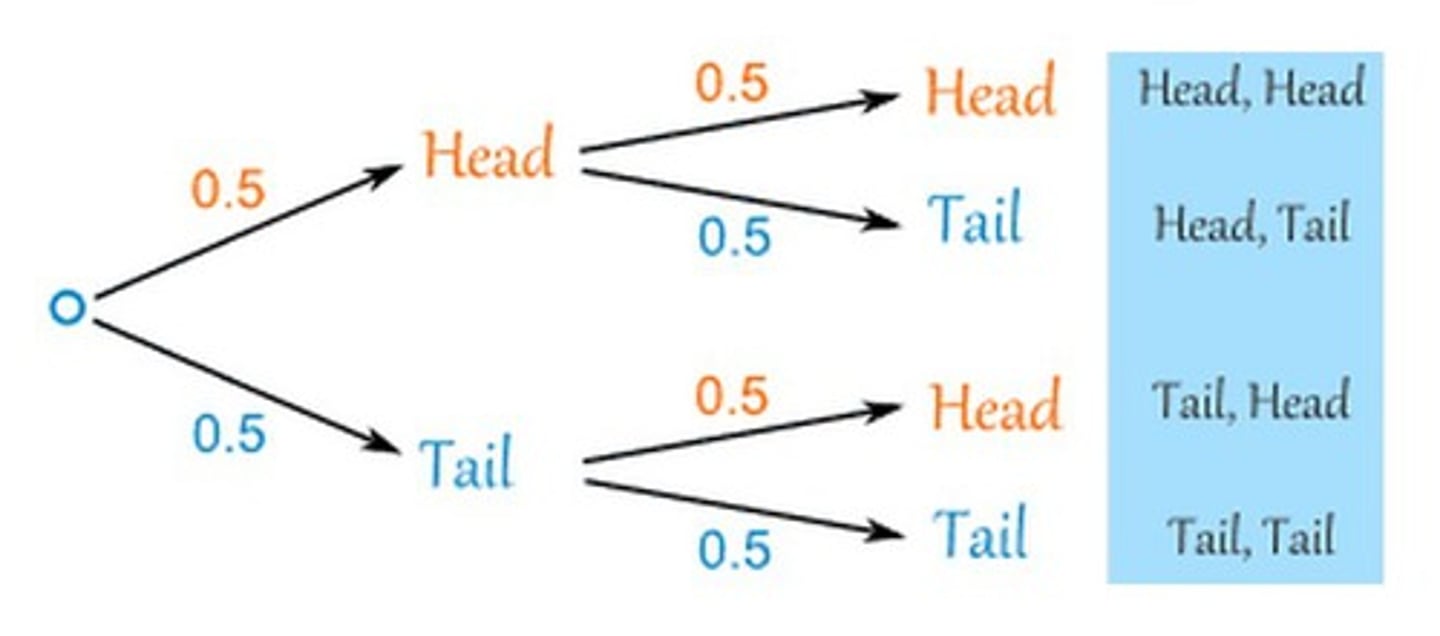
Tree diagrams

A diagram that is shaped like a tree and is used to show the outcomes of a situation or experiment.

Relative Frequency/Experimental Probability

number of outcomes/total trials

Long-run proportion

The experimental probability for a sufficiently large number of trials

Expected number of occurance

probability x number of trials

Mode

the most frequently occurring score(s) in a distribution

Stem and leaf plots

best suited for small sets of data and are especially useful for comparing 2 sets of data

Rule for finding the median

N+1/2

Skewed

not straight, crooked, slanting

Symmetrical

Well proportioned; balanced; the same on both sides

Categorical Nominal

No order required in a category eg. colours

Categorical Ordinal

Categories have a logical order eg. high, medium, low

Numerical DIscrete

data with a limited amount of numbers eg. children in a family

Numerical Continuous

Data can take any value in a given range eg. time taken to complete a race

How much is a quartile?

25%

What is a quartile?

A division of the total into four intervals, each one representing one-fourth of the total.

What does the second quartile represent?

Median

Simple random sampling

every member of the population has an equal probability of being selected for the sample

Systematic Sampling

Every nth item in the target population is selected, regular intervals.

Stratified Sampling

a variation of random sampling; the population is divided into subgroups and surveyed in that group

Histogram

a bar graph depicting a frequency distribution

Bar chart

a chart with bars whose lengths are proportional to quantities

a^n

1/a^n

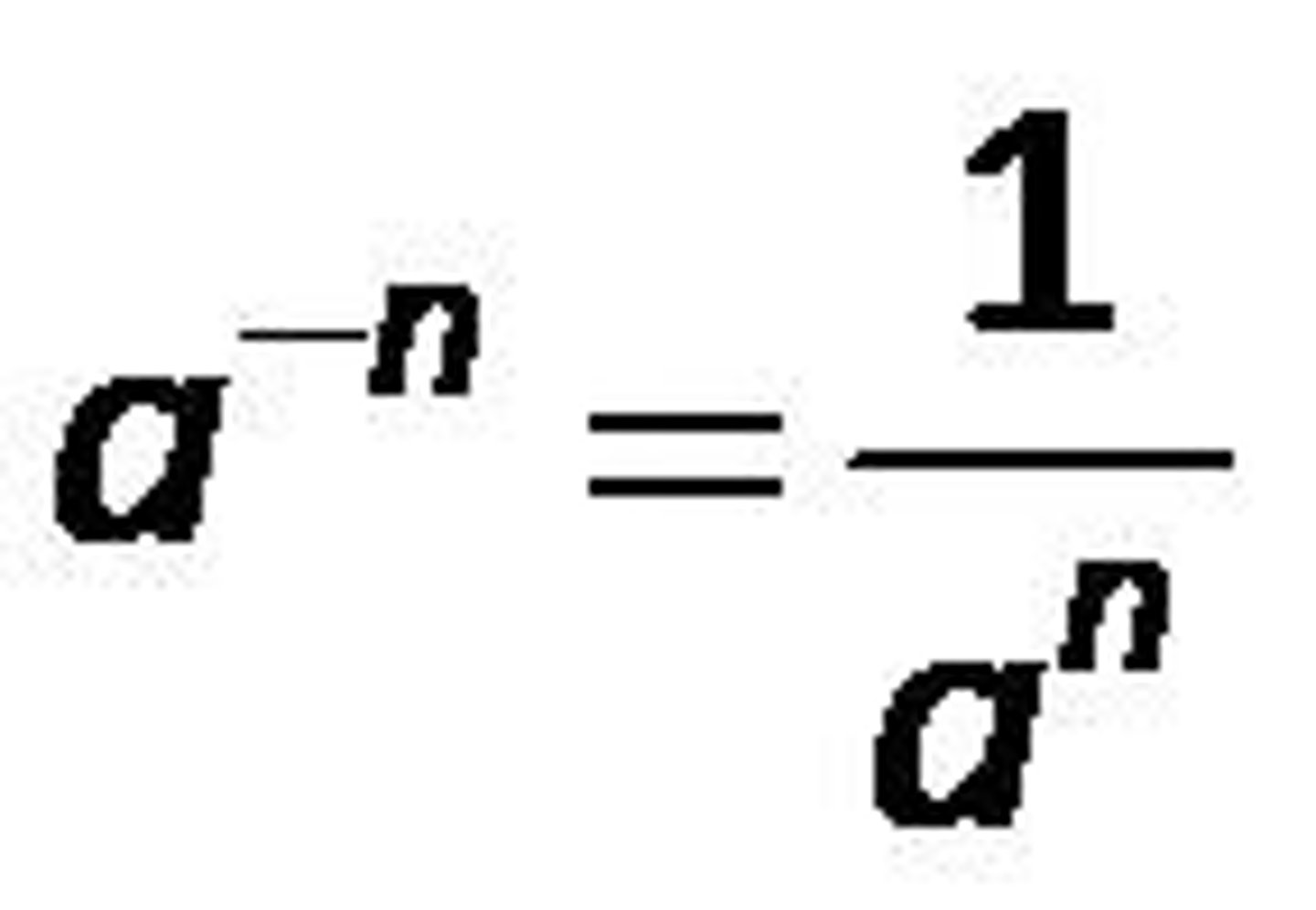
1/a^n

a^n

x^a/b

b√x^a

x^-a/b

1/x^a/b

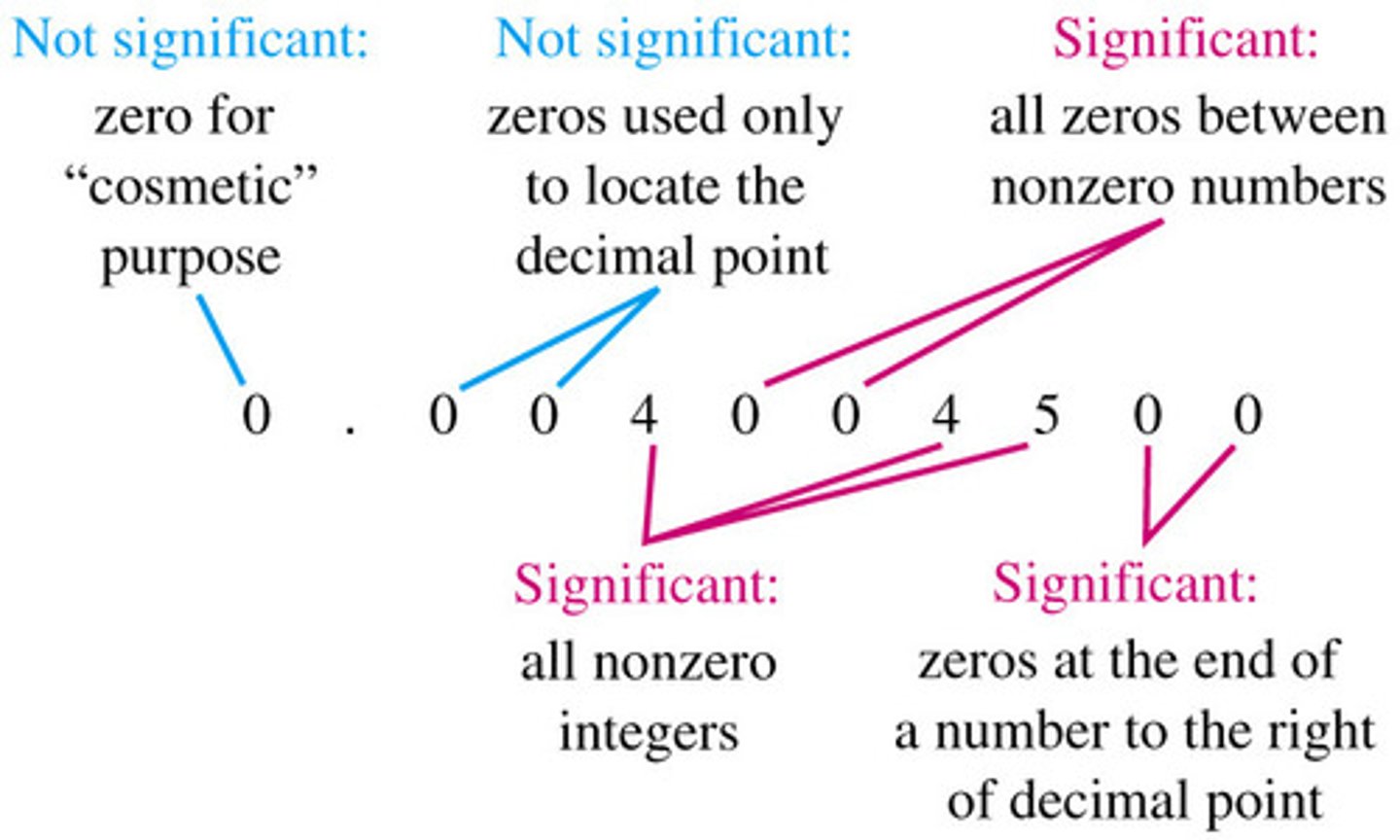
Significant numbers

any number that is not a 0, sandwiched 0s, trailing 0s when there is a decimal place; NOT trailing 0s without a decimal place and leading 0s.

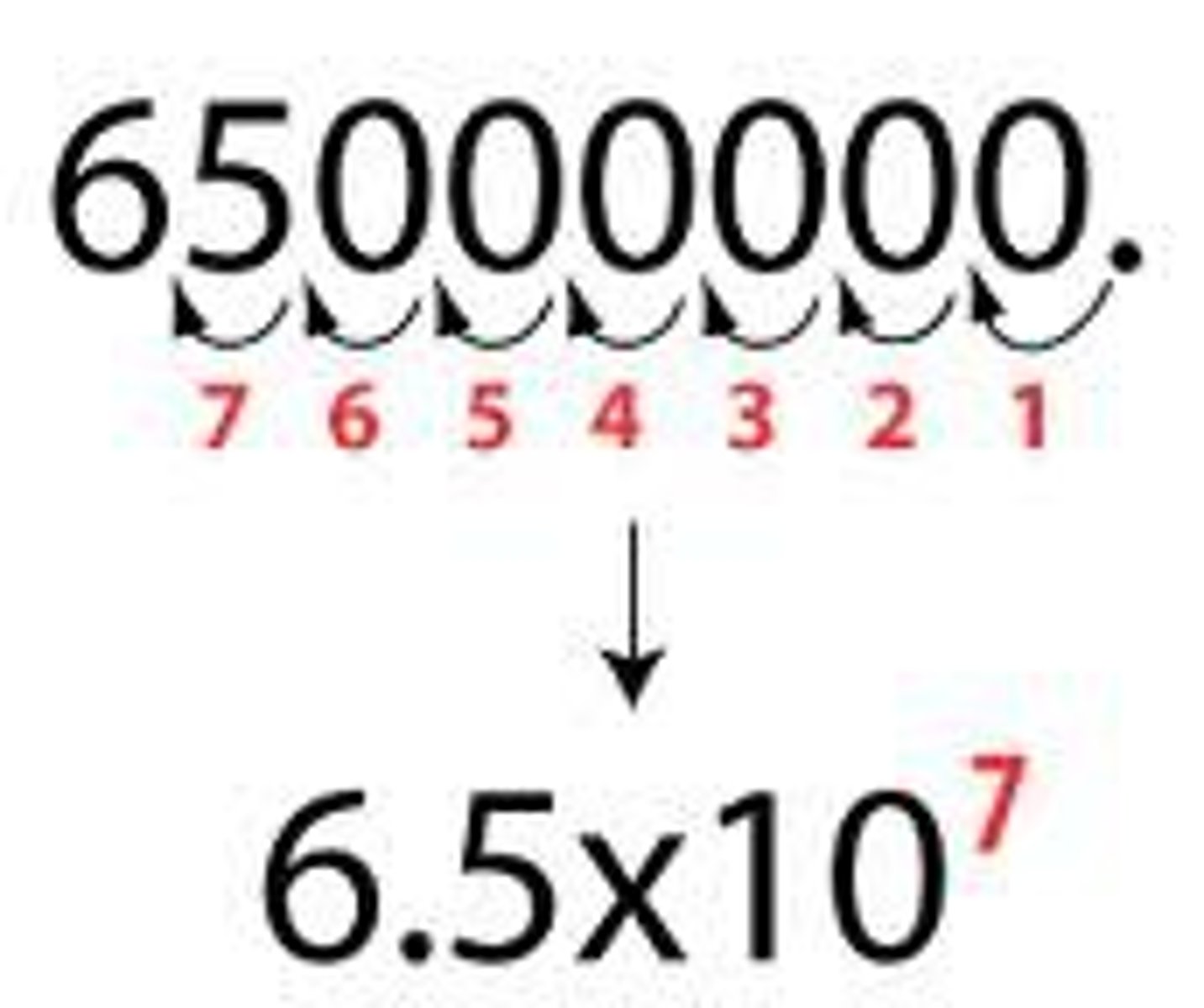
Scientific notation

A method of writing or displaying numbers in terms of a decimal number between 1 and 10 multiplied by a power of 10.

Negative scientific notation

A method of writing or displaying numbers in terms of a decimal number between 1 and 10 multiplied by a power of 10 with negative indice.

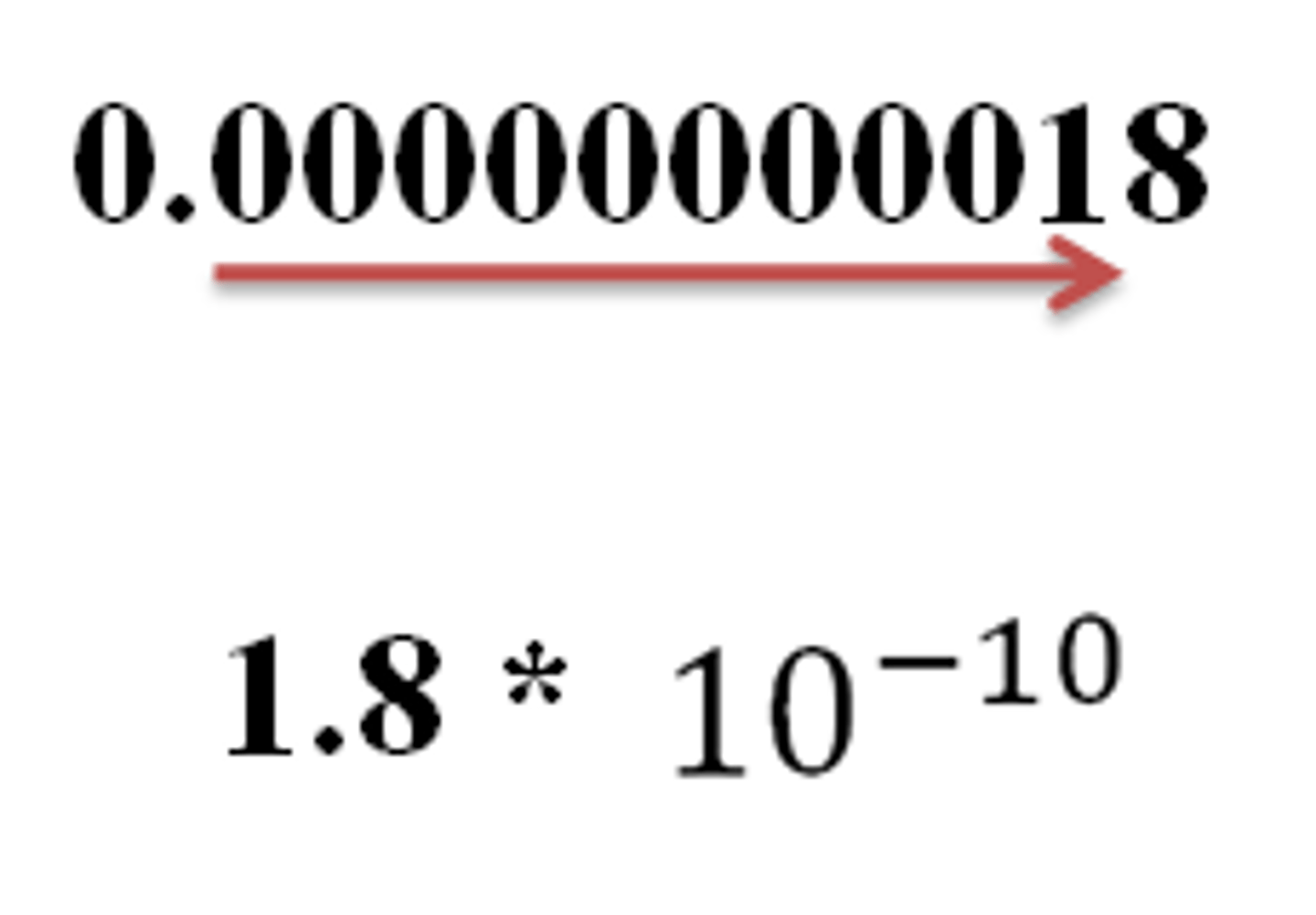
How to simplify surds

Find the common square number and pull that out.

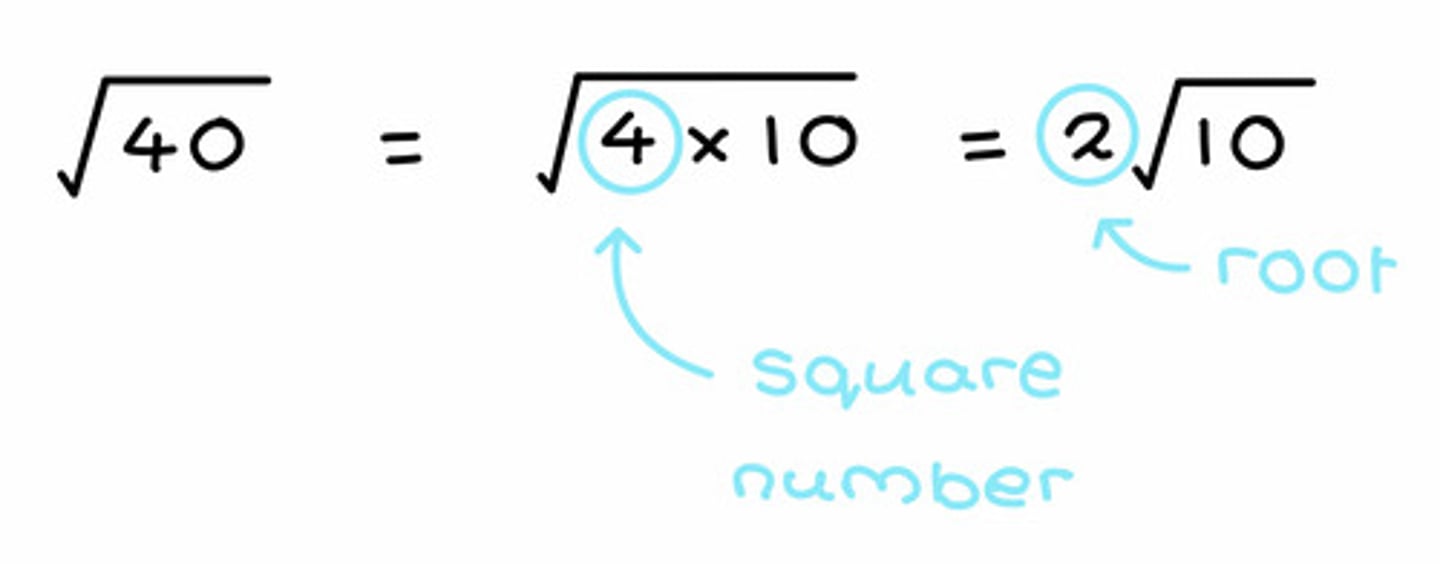
True of false: You can only add or subtract like surds

True

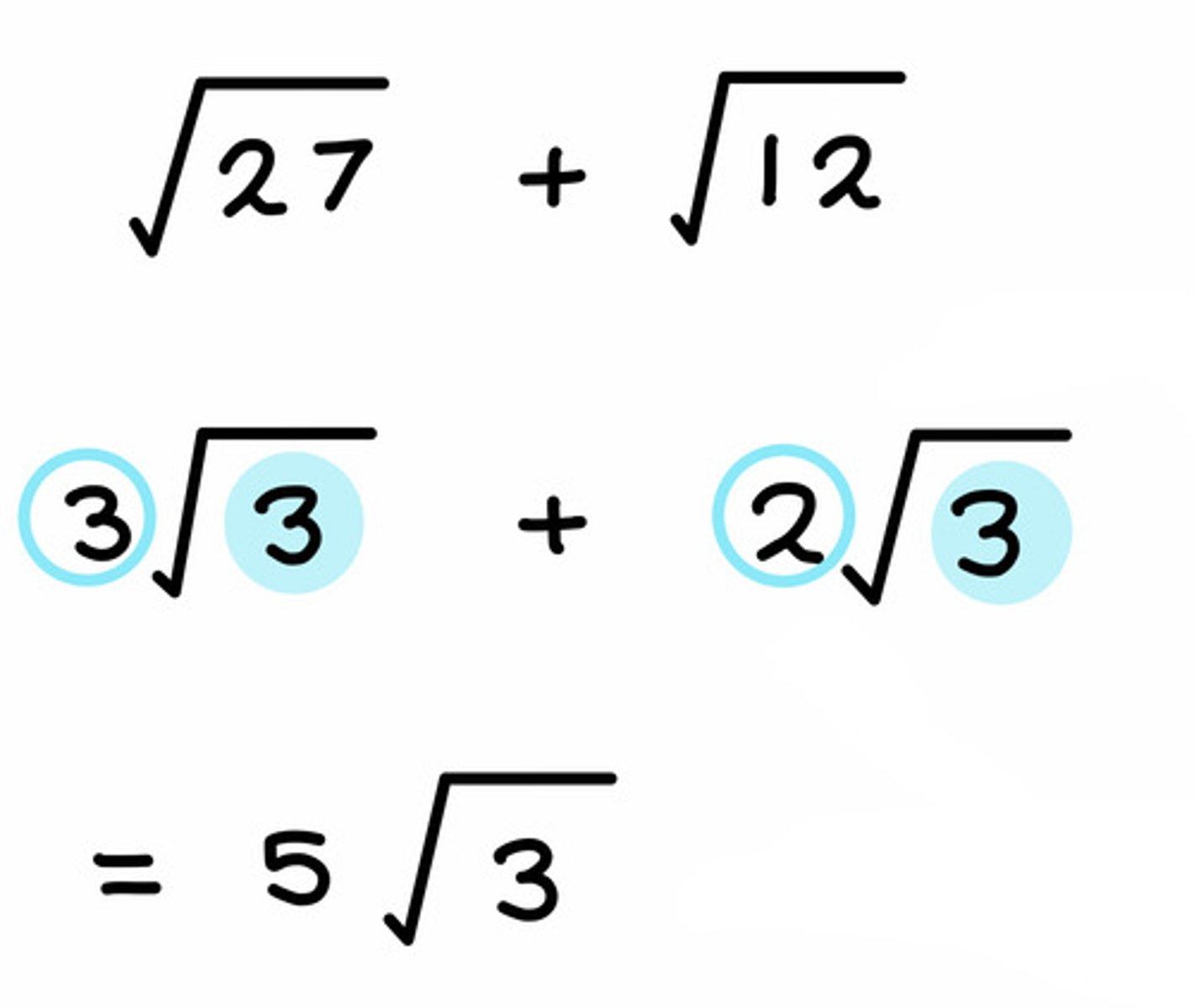
BIDMAS

Brackets, Indices, Division, Multiplication, Addition, Subtraction.

What is an error?

An incorrect measurement

Formula to find the error

Error=Measurement-Actual Value

Formula to find the percentage of an error

Percentage error = Error/Actual value x 100

Upper Limit for measurement

recorded measurement + 0.5 x smallest unit of measure

Lower Limit for measurement

recorded measurement - 0.5 x smallest unit of measure

Cross-section

What a shape is sliced, what shape appears?

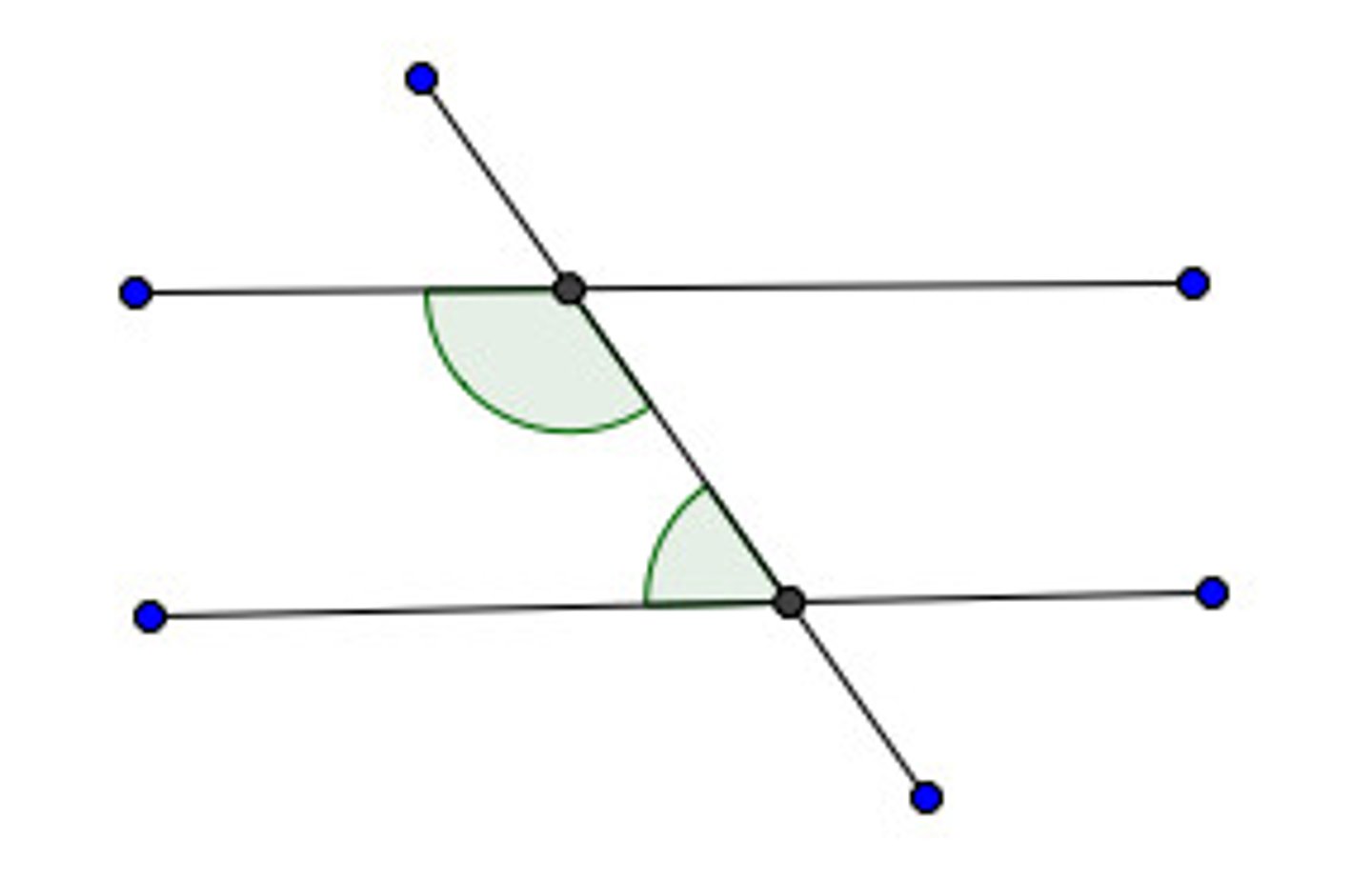
Corresponding Angles

Angles in the same place on different lines

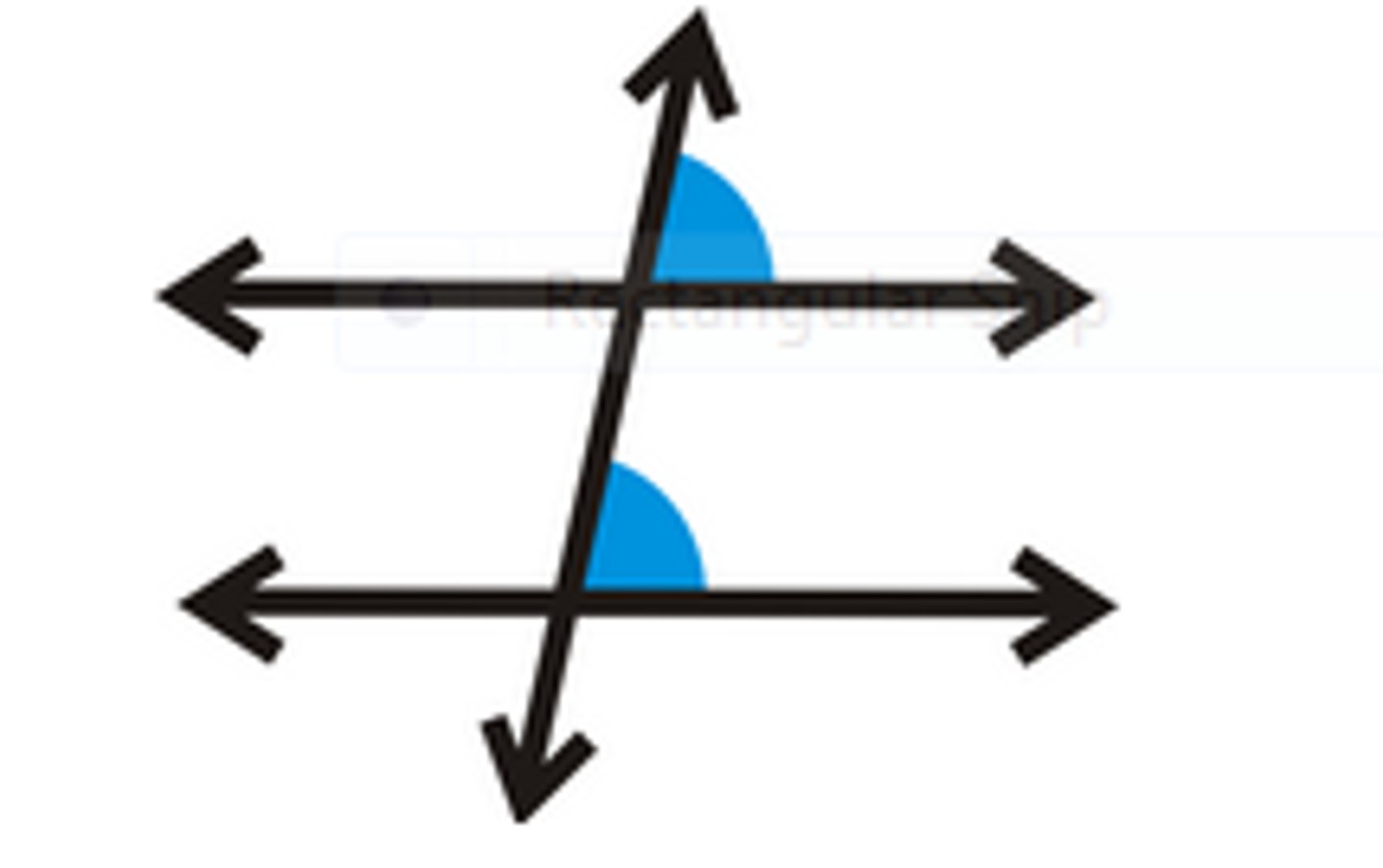
Alternate Interior

angles between 2 lines and on opposite sides of a transversal

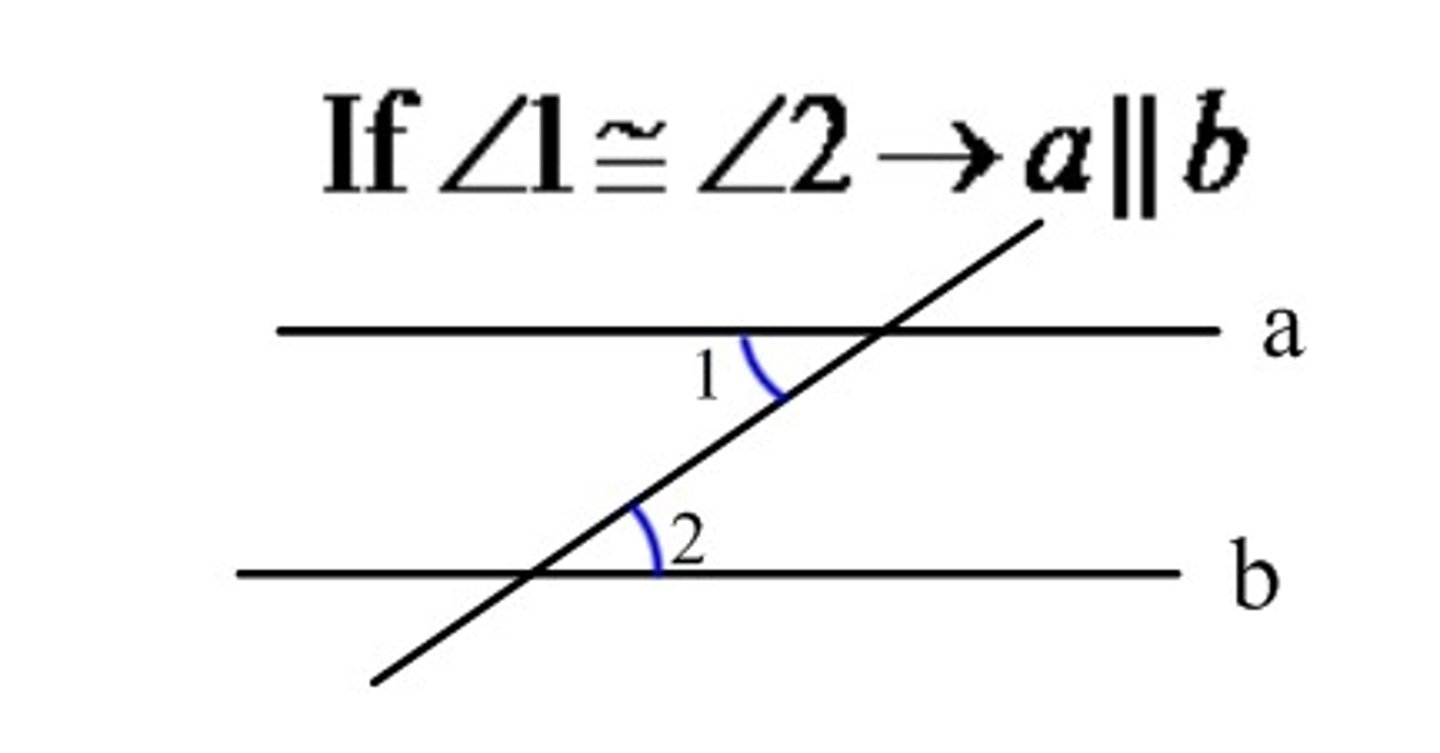
Alternate Exterior

Angles that lie outside a pair of lines and on opposite sides of a transversal.

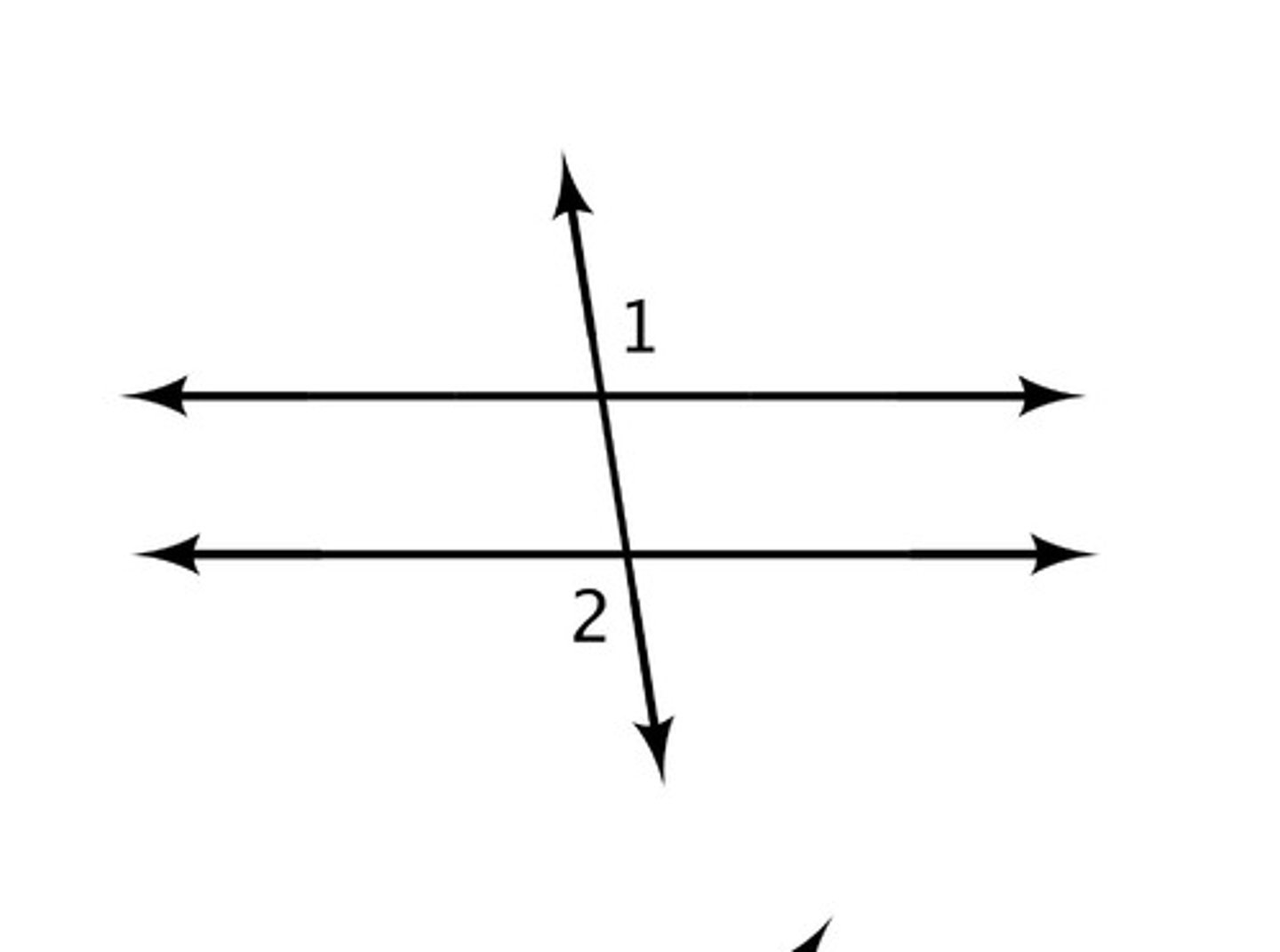
Co-interior angles

add to 180

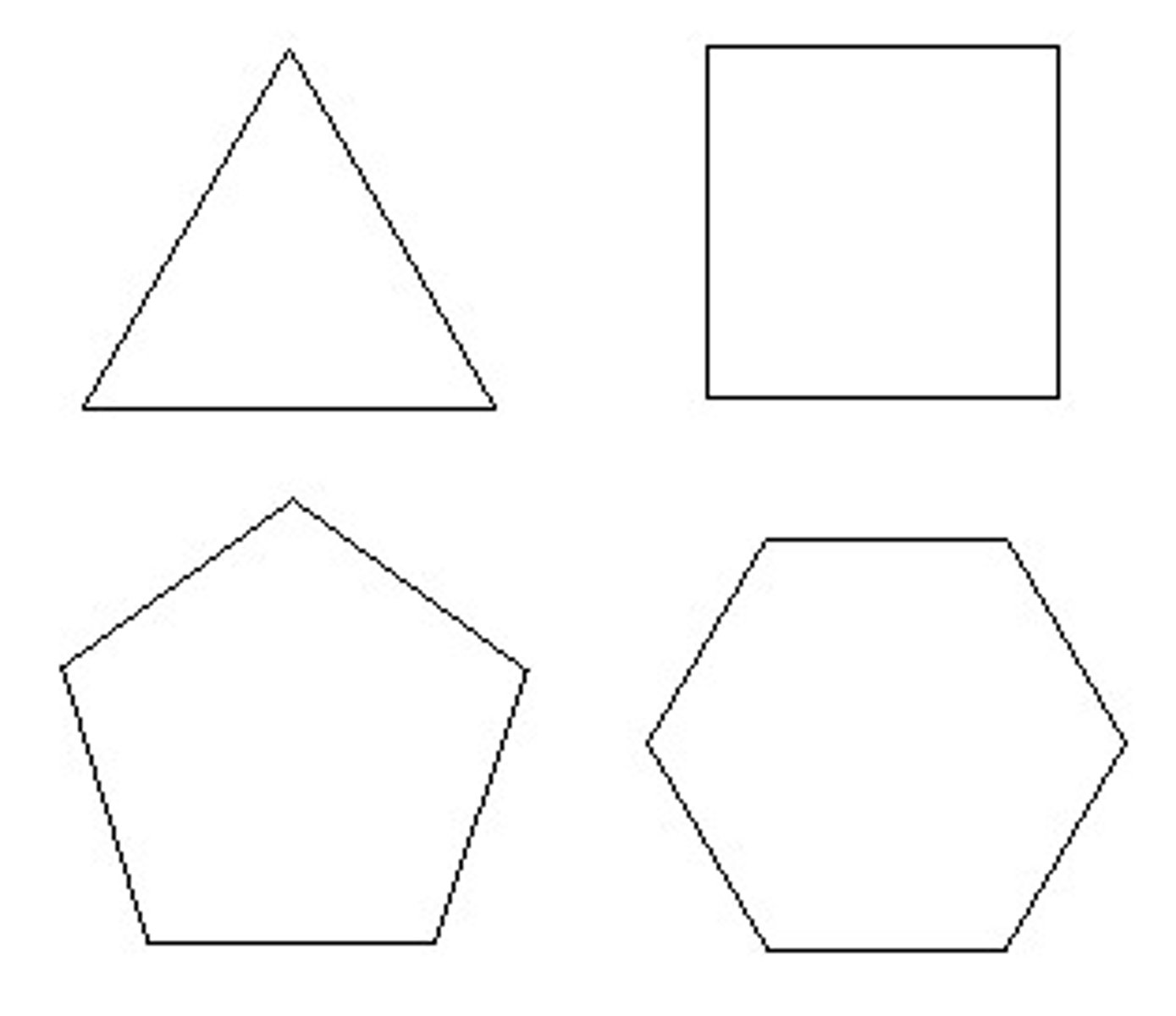
Convex polygons

A polygon in which each interior angle has a measure less than 180 degrees

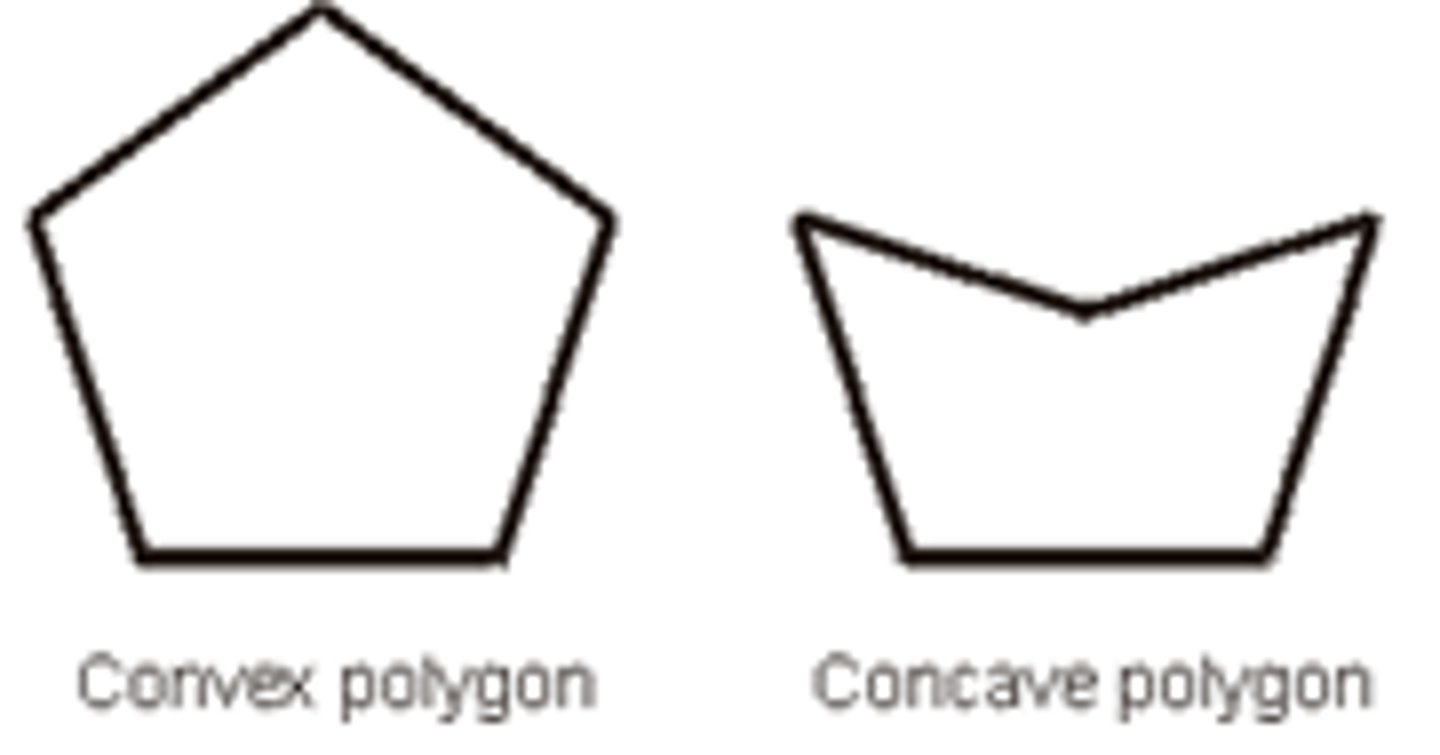
Non-convex polygons/concave

A polygon in which not all interior angles have a measure less than 180 degrees

Formula to find the degrees of a polygon

(n-2)x180

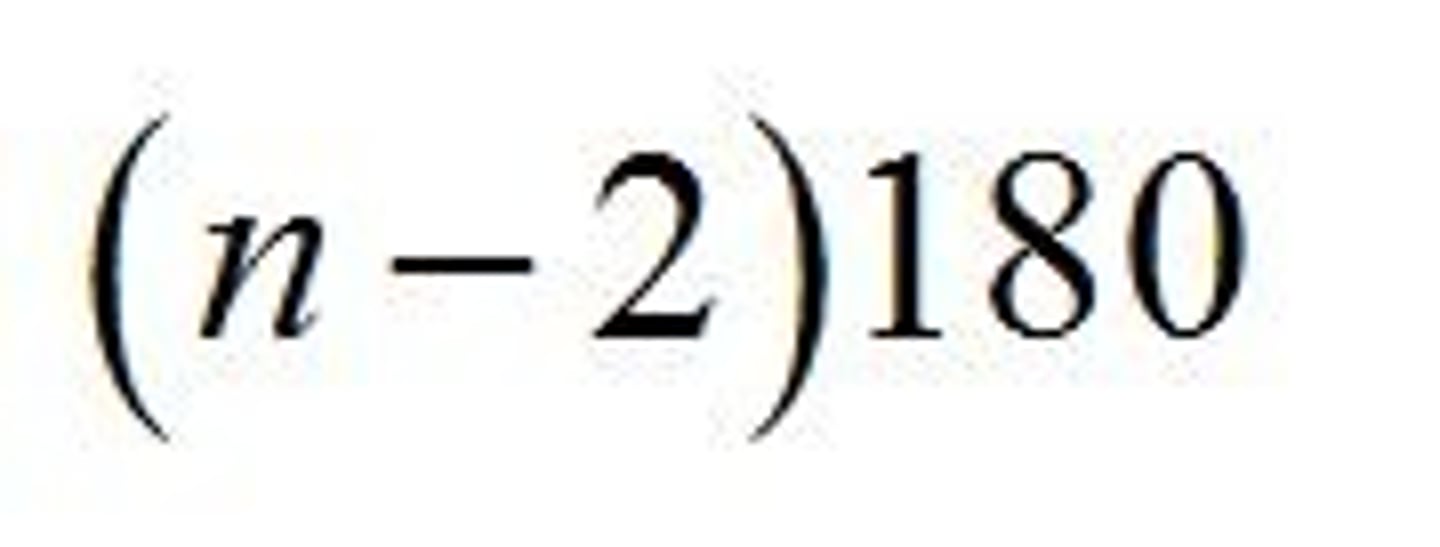
Congruent figures

Figures that have the same size and shape

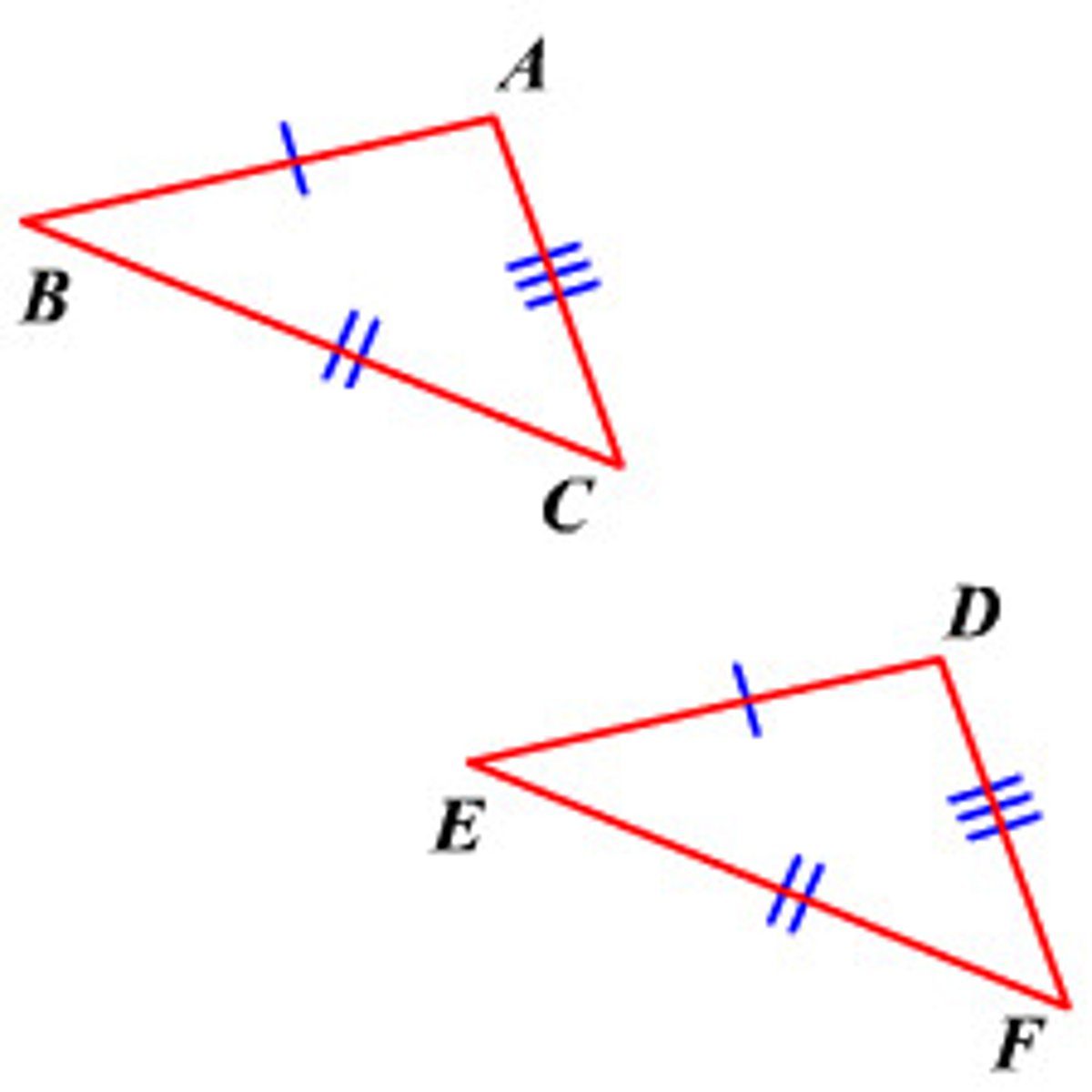
SSS

side side side

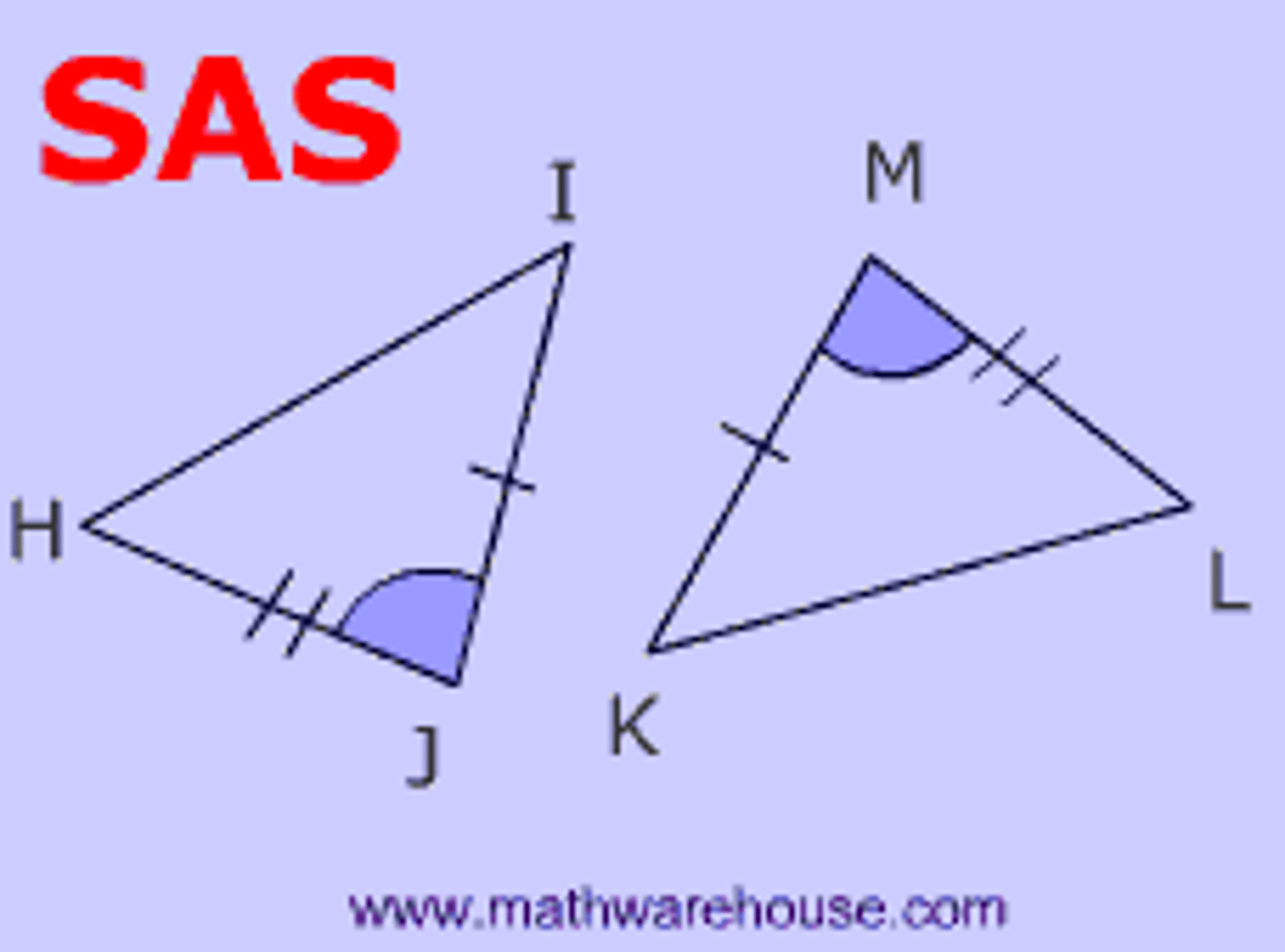
SAS

side angle side

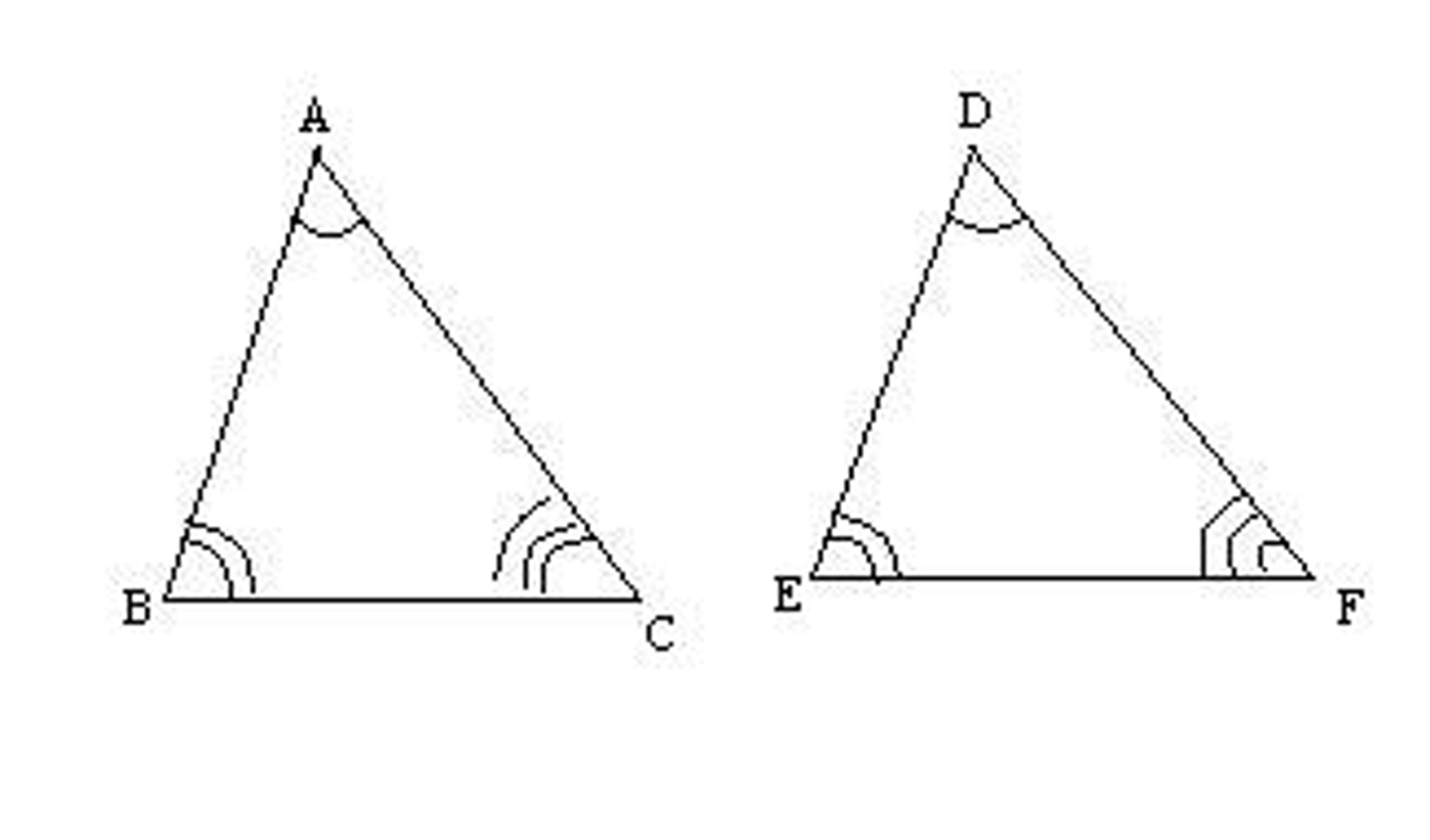
AAA

angle angle angle

RHS

Right Angle, Hypotenuse, Side

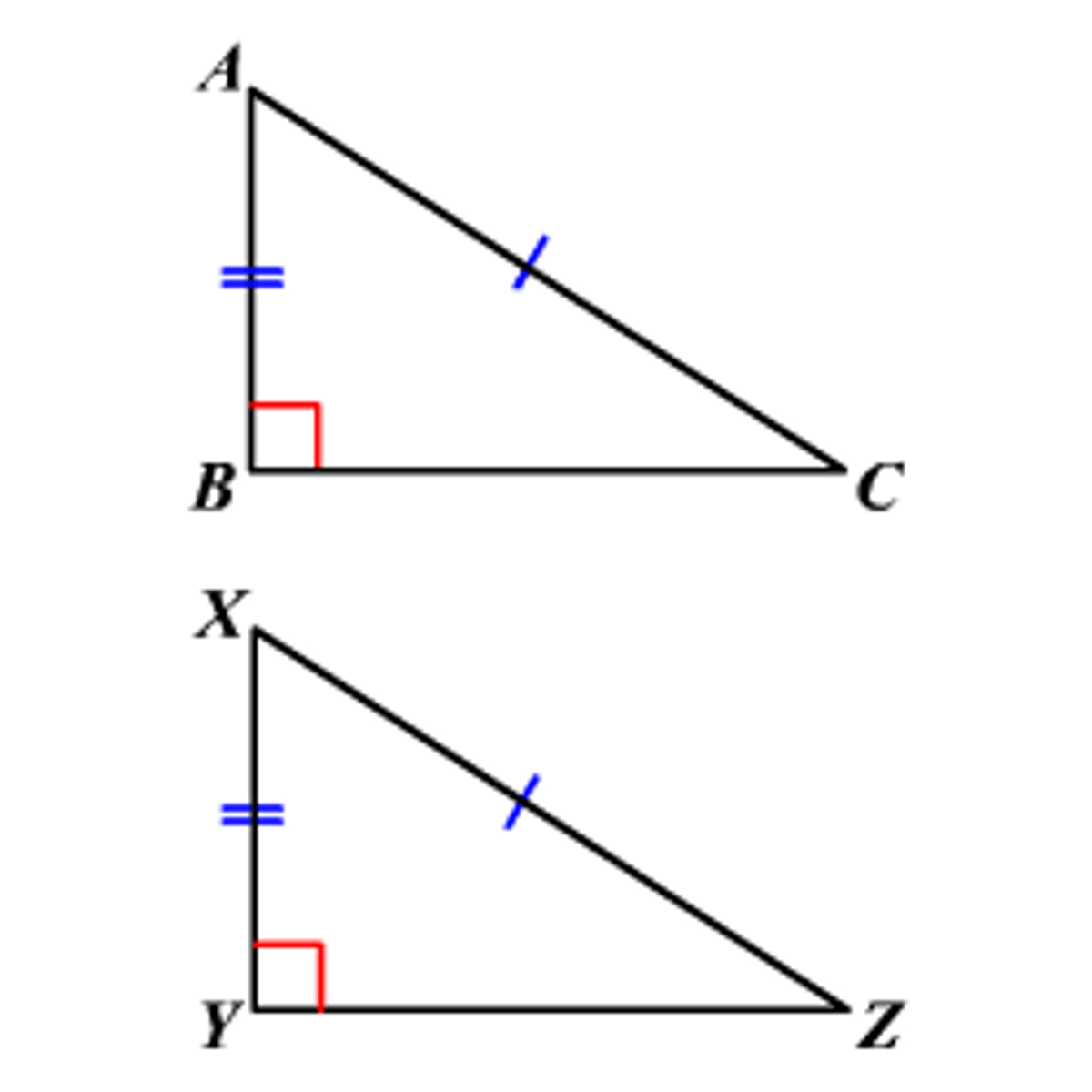
Congruency symbol

≅

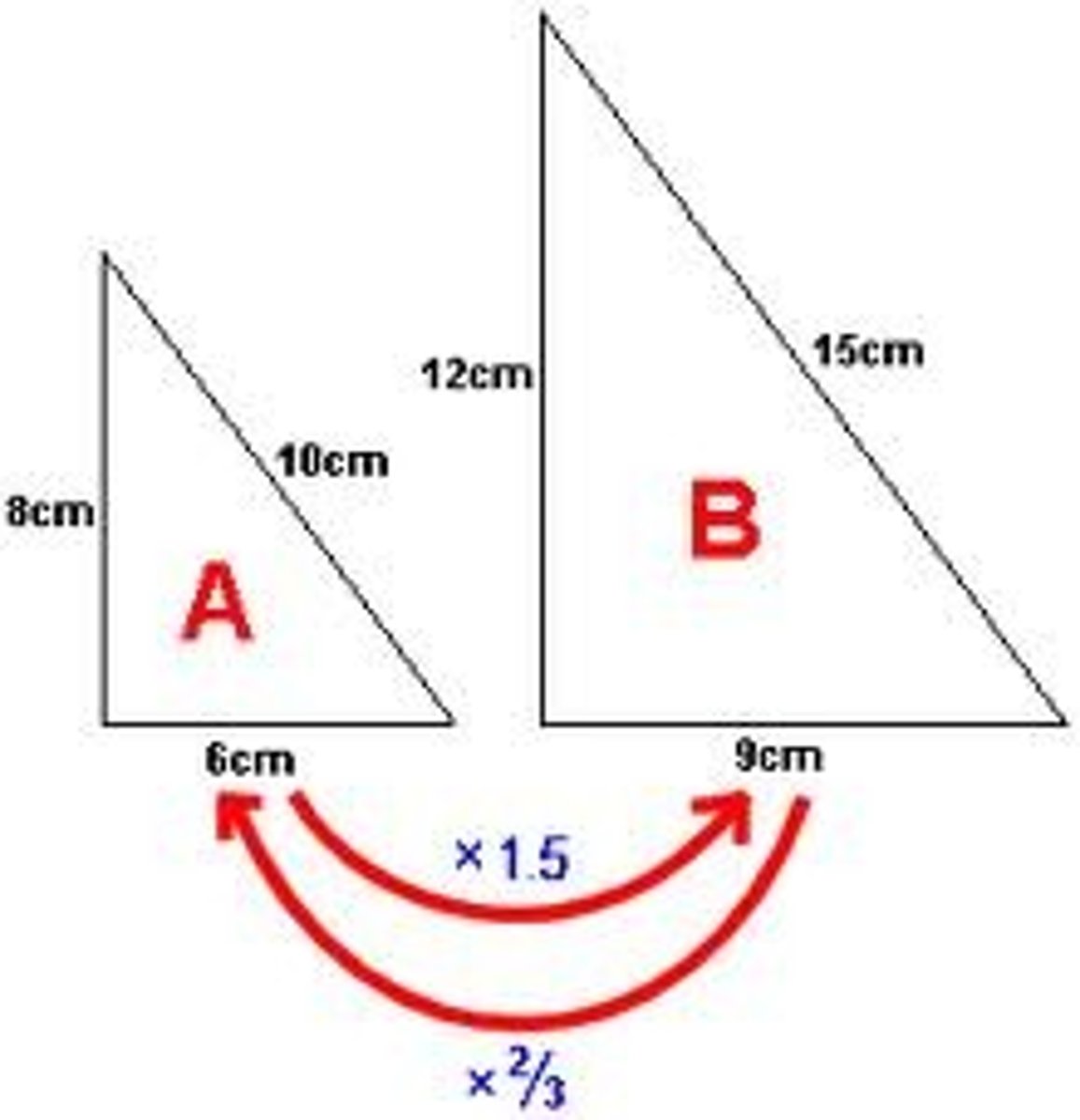
Scale factor

Image length/Original Length

Pythagoras Theorem- Hypotenuse

a²+b²=c²

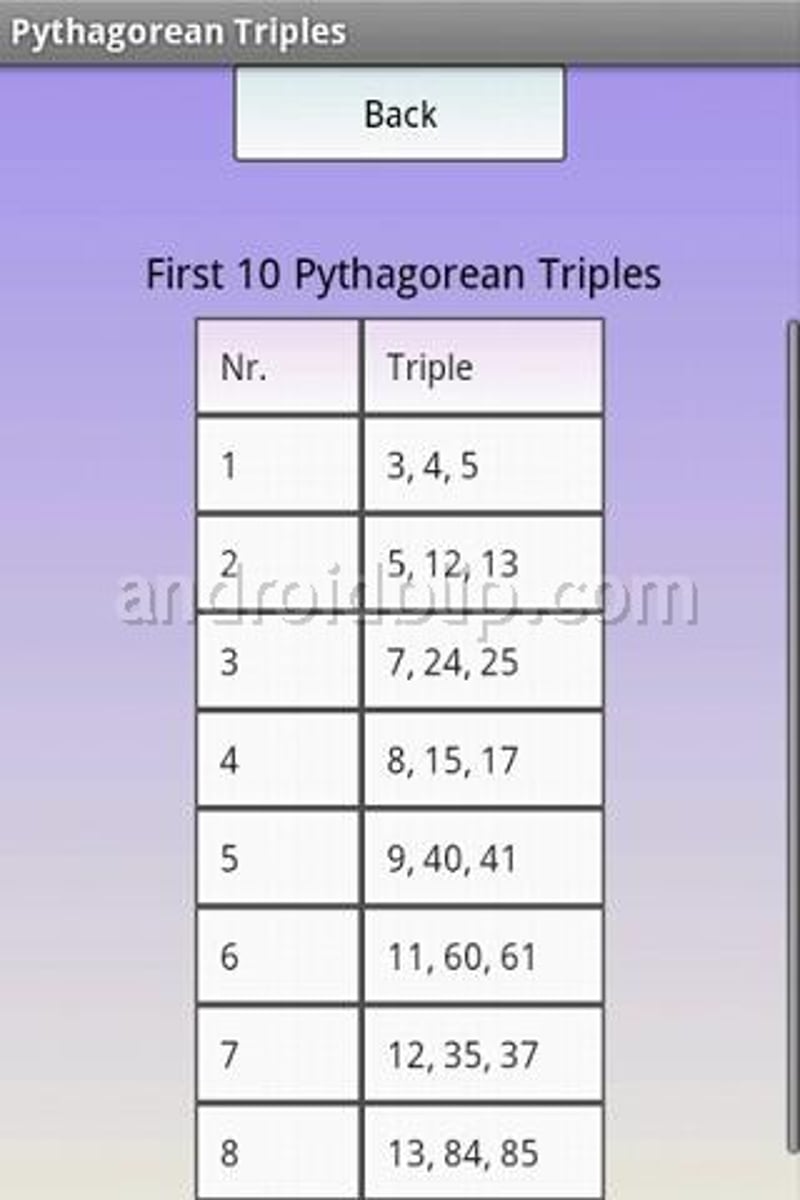
Pythagorean Triad

A set of three numbers that make a right angled triangle.

Pythagorean Triads

3,4,5/6,8,10/12,16,20

Pythagoras Theorem- Shorter Sides

c²-a²=b² or c²-b²=a²

How to find if a triangle is acute or obtuse

Find the third side and using Pythagoras theorem, if the predicted side is smaller than the other sides (acute) and if it is bigger (obtuse).

SOH-CAH-TOA

sin= opposite/hypo

cos= adjacent/hypo

tan= opposite/adjacent

How inverse trigonometry works

Inverse sine (sin−1) , inverse cosine (cos−1) and inverse tangent (tan−1) can be used to find angles in right-angled triangles.

Eg. sinθ=a/c means θ=sin⁻¹(a/c)

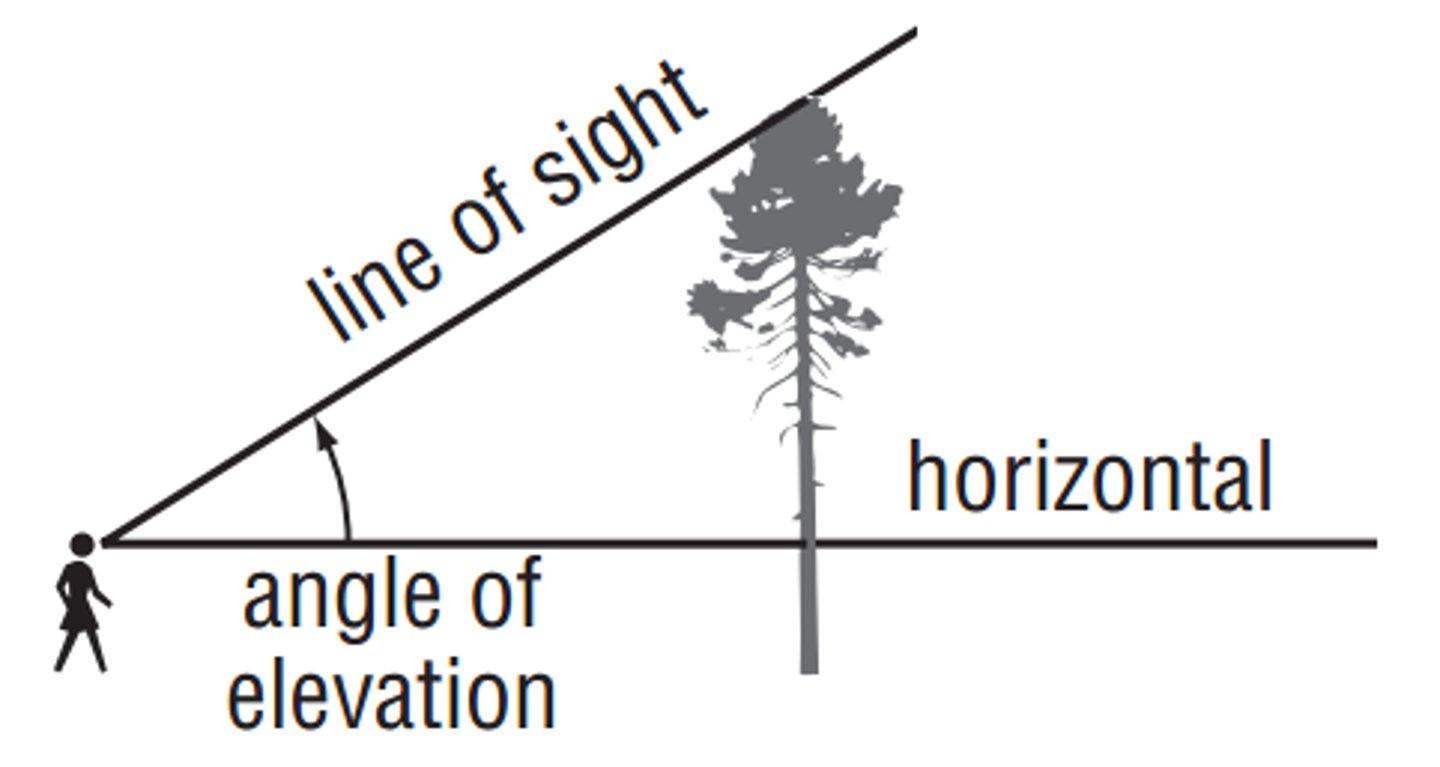
Angle of Elevation

Angle between horizontal line and the line of sight of the observer to an object above the observer.

Angle of depression

Angle between horizontal line and the line of sight of the object to an object below the observer.

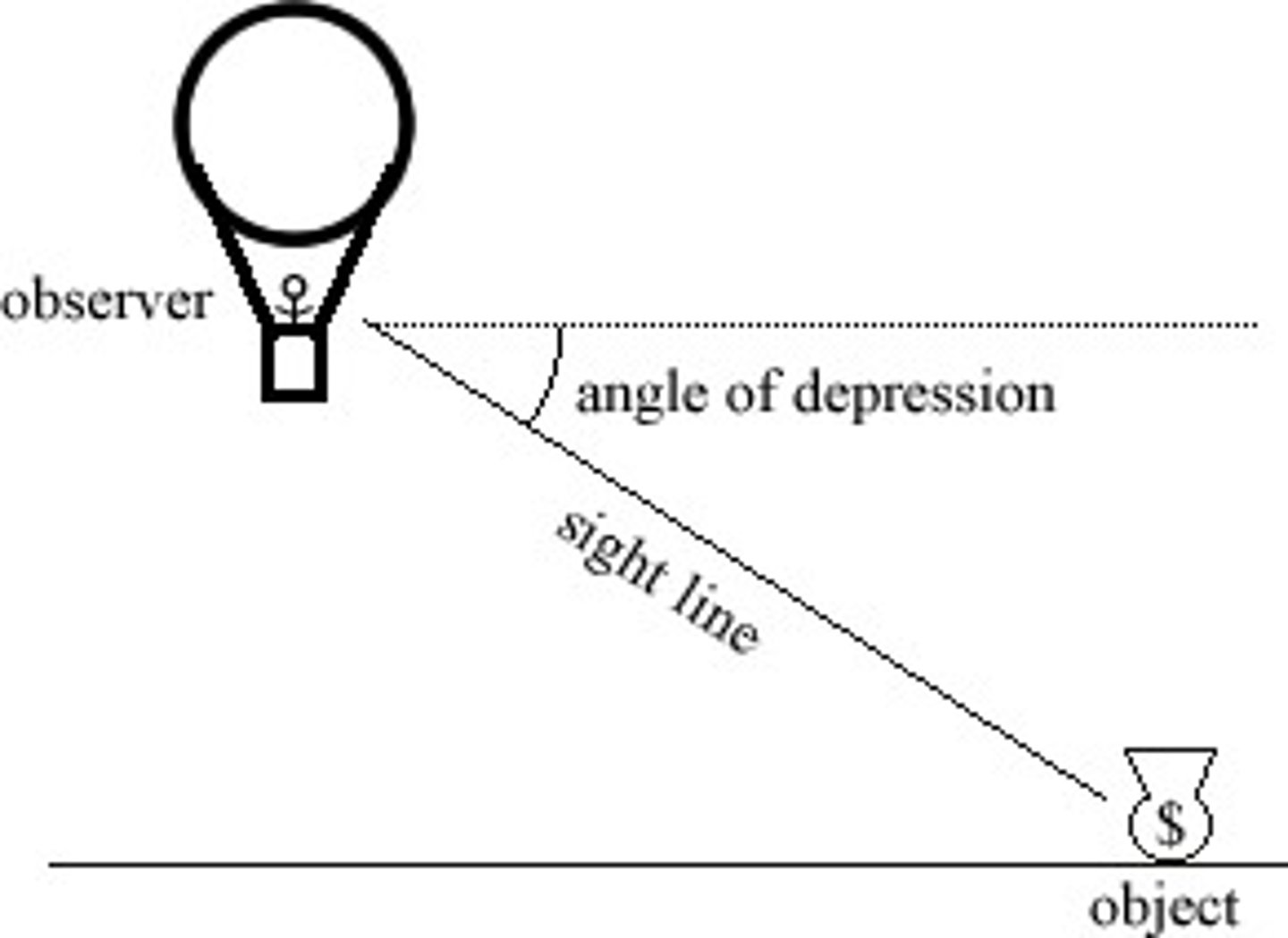
Where are angles of elevation measure from?

Angles of elevation or depression are ALWAYS measured from the horizontal!

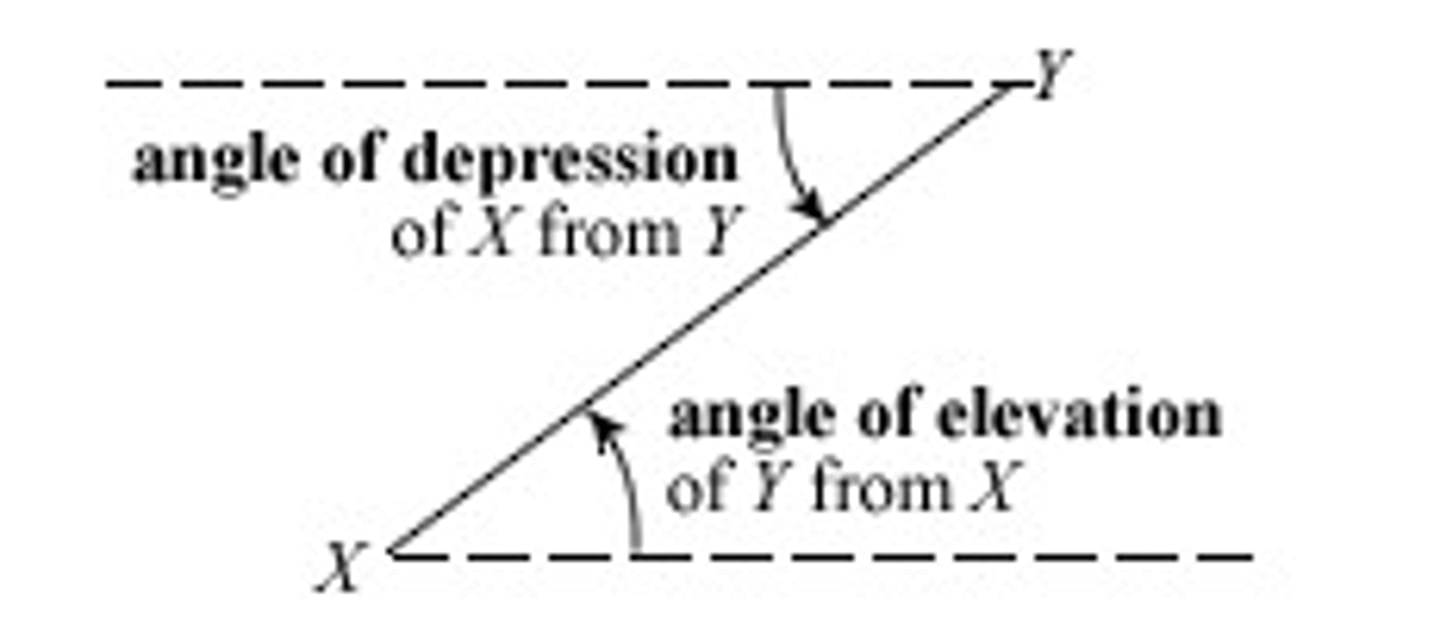
Elevation and Depression

In this diagram the angle of elevation of B from A is equal

to the angle of depression of A from B. They are equal

alternate angles in parallel lines.

How do you find if something is a Pythagoras Triad?

You try the Pythagoras theorem on it:

Eg. Find is 3,4,5 is a Pythagoras Triad

3²+4²=5²

9+16=25

How to find the coordinates of the x and y intercept in parabolas

Make the other term 0

How to find the axis of symmetry

(a+b)/2

How to solve a system of equations on cas

Menu-Algebra-Solve System Of Equations

How to graph linear equations on cas

Menu-Graphs-f1(x)

Dilation

When something is multiplied by a particular factor

Reflection

When something changes from concave up to concave down

Translation

Shifting every point horizontally and/or vertically

Vertex Form of Quadratic Equations

y=a(x-h)²+k

Circles Area

πxr²