DA110 WEEK 1

WEEK 1

Algorithm

A

well-defined list of

finite

unambiguous steps

for solving a problem.

Data Structure

Defines a data collection of

data values,

logical relationship among them, and the

operations that can be applied on the data.

Scenario I characteristic

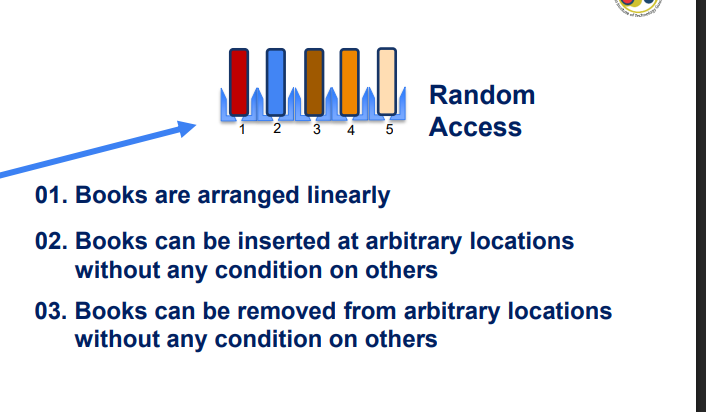
Scenario II characteristic

Scenario III characteristic

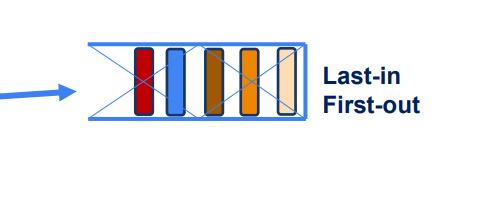
Scenario II

Last-in, First-out

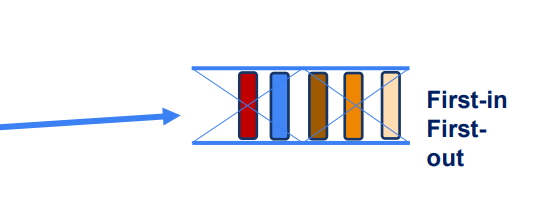
Scenario III

First-in, First-out

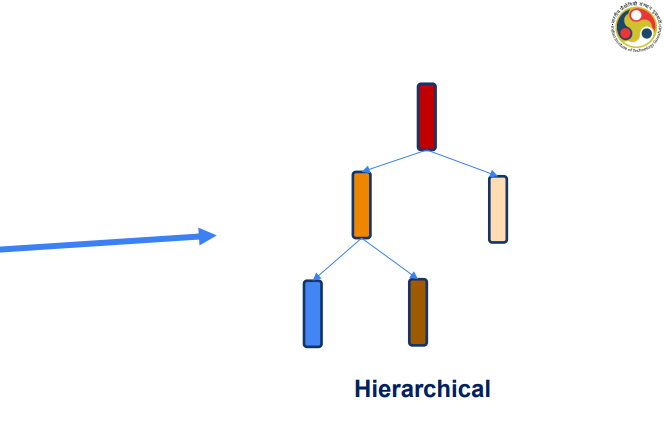
Scenario IV

Hierarchical structure used to organize information based on levels of

importance or authority.

Scenario V

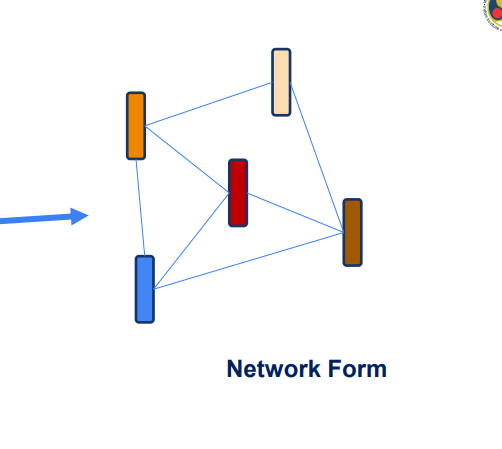
Network Form : A type of organizational structure characterized by a decentralized network of interconnected organizations or individuals that collaborate to achieve common goals.

Data Structure

Organization + Operations + Algorithm

Program

Data Structure + Algorithm

Data

Collection of raw facts

Data element

It is a logical unit adding up to a data.

Data type

It specifies the type of value or values of data elements forming a data.

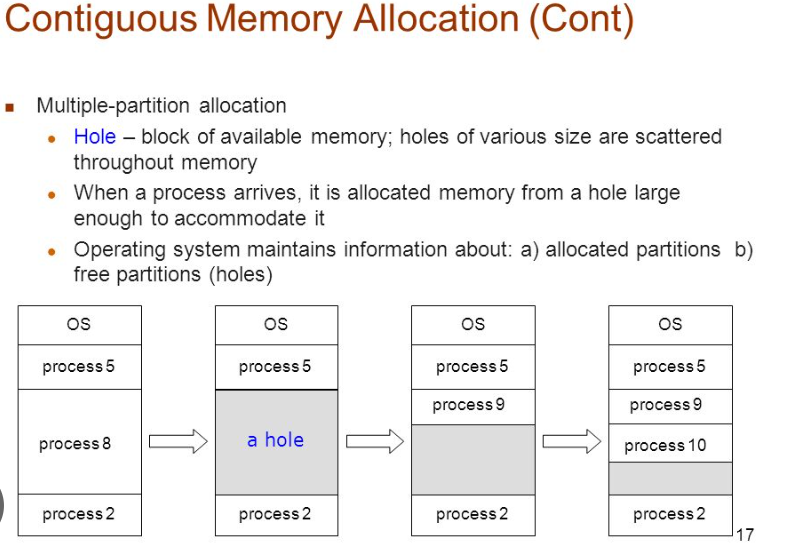
Contiguous Memory Allocation

Pattern where the data elements of a data structure will be stored at contiguous (next or together in sequence.) memory locations in memory

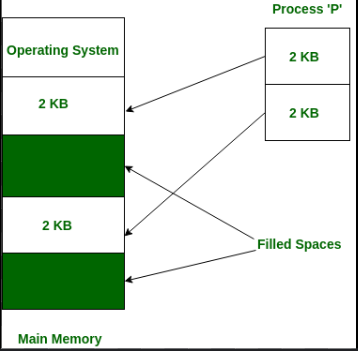
Non-Contiguous Memory Allocation

Pattern where the data elements of a data structure will be stored at non-contiguous arbitrary locations in memory.This method allows for efficient use of memory by allocating space as needed without requiring contiguous blocks.

Contiguous Memory Allocation advantages

Advantages include

ordering,

Random Access Memory, and

no additional memory needed for management,

leading to efficient CPU usage and faster access times.

Contiguous Memory Allocation disadvantages

Disadvantages include

Static Allocation,

OS Defragmentation,

Un-used Memory and

Large RAM requirement

Non-contiguous Memory Allocation Advantages

Advantages include better memory utilization, reduced fragmentation, and flexibility in allocating memory blocks.

Non-contiguous Memory Allocation Disadvantages

Disadvantages include Additional memory is needed and Data Access may need to traverse through the other data elements.

Creation

Create an empty instance of a data structure.

Insertion

Insert a data element into an instance of a data structure.

Deletion

Delete a data element from an instance of a data structure.

Updation

Change the value of a data element

Searching

Search for the existence or non-existence of a data element.

Traversal

Visits every data element in an instance of a data structure.

Sorting

Order the data elements either in ascending or descending order.

Merging

Combines data elements of two or more data structures to one.

Input Specified

Input to an algorithm should be clearly specified. An algorithm can have zero or more inputs.

Output Specified

Output of an algorithm should be clearly specified. An algorithm has one or more outputs.

Definiteness

Every step of an algorithm should be unambiguous.

Finiteness

Every algorithm should terminate after a finite number of steps.

Effectiveness

The steps of an algorithm should be sufficiently basic and doable by a person in a finite time with pencil and paper.

Complexity of Algorithm

Includes Time Complexity and Space Complexity.

Classification of Data Structure

Includes Primitive vs Non-primitives, Linear vs Nonlinear, Homogeneous vs Heterogeneous, and Static vs Dynamics.

Non-primitives data structures

Array, Linked List, Stack and Queues, Tree/Binary tree, Hash, Graph

Array

A collection of a finite number of homogeneous data elements stored at contiguous memory locations.

INDEX

Defines the location and ordering of the data elements in an array.

LOWER BOUND

Defines the location of the first element in an array.

UPPER BOUND

Defines the location of the last element in an array.

SIZE (of an array)

UPPER BOUND – LOWER BOUND +1

Types of Array

One-Dimensional, Multi-Dimensional

2(two)-Dimensional array

An array of one dimensional arrays.

3(three)-Dimensional array

An array of two dimensional arrays.

Number of 1D arrays

Number of rows in a 2D array.

Number of Columns

The number of elements in each 1D array

Size of 2D arrays

|Columns| x |Rows|

Size of 3D array

|Plates| x |Columns| x |Rows|

BASE address

The address of the first element in memory

𝐸𝑓𝑓𝑒𝑐𝑡𝑖𝑣𝑒 𝐴𝑑𝑑𝑟𝑒𝑠𝑠 𝑜𝑓 𝐴 𝑖 for 1D arrays

A = 𝑏𝑎𝑠𝑒 𝑎𝑑𝑑𝑟𝑒𝑠𝑠 + (𝑖 − 𝐿𝐵) × 𝑘

Row major order

Arranging the elements in memory row-wise.

Column major order

Arranging the elements in memory column-wise.

Address of 𝐴 𝑖 𝑗 for 2D arrays in Row major order

𝐴𝑑𝑑𝑟𝑒𝑠𝑠 𝑜𝑓 𝐴 𝑖 𝑗 = 𝐵𝑎𝑠𝑒 𝑎𝑑𝑑𝑟𝑒𝑠𝑠 + 𝑖 − 𝐿𝐵𝑅 × 𝐶𝑜𝑙 + 𝑗 − 𝐿𝐵𝐶 𝑘

Address of 𝐴 𝑖 𝑗 for 2D arrays in Column major order

𝐴𝑑𝑑𝑟𝑒𝑠𝑠 𝑜𝑓 𝐴 𝑖 𝑗 = 𝐵𝑎𝑠𝑒 𝑎𝑑𝑑𝑟𝑒𝑠𝑠 + 𝑗 − 𝐿𝐵𝐶 × 𝑅𝑜𝑤 + 𝑖 − 𝐿𝐵𝑅 𝑘

Operations on Array Data Structure

Create, Display/Traverse, Search, Deletion, Modification/Update, Insertion

Create Operation

It creates an empty Array, allocates the required memory in RAM

Two ways to create an array in C

Static memory allocation during compile time or dynamic memory allocation during run time.

Compile time

The memory is reserved at compile time.

Run time

Created using a function called malloc.

Display/Traversal Operation

Visit all the elements in the array

Search Operation

Given an element, check if it is present in the array

Time Complexity

Worst Case: The element is not found or found at the last index. Time complexity is 𝜃(𝑛)

Insertion Operation

Insert an element at an arbitrary index 𝑖 ≥ 0.

Deletion Operation

Delete an element from an arbitrary index 𝑖 ≥ 0.

Update Operation

Replace the value at 𝑖 ≥ 0 by another value.

Sparse Matrix

A special type of matrix with a relatively high proportion of zero elements.

Some Special Sparse Matrix

Triangular Matrices, Diagonal and Tri-diagonal Matrices

Task for Left Lower Triangular Matrix

Store only the non-zero elements in memory

𝐴 of A[ i ][ j ] for the Left Lower Triangular Matrix

𝑖 𝑗 = 𝑏𝑎𝑠𝑒 𝑎𝑑𝑑𝑟𝑒𝑠𝑠 + ቇ 𝑖 − 𝐿𝐵𝑅)(𝑖 − 𝐿𝐵𝑅 + 1 2 + (𝑗 − 𝐿𝐵𝐶 × 𝑘

Right Lower Triangular Matrix

𝑖 𝑗 = 𝑏𝑎𝑠𝑒 𝑎𝑑𝑑𝑟𝑒𝑠𝑠 + 𝑖 − 𝐿𝐵𝑅)(𝑖 − 𝐿𝐵𝑅 + 1 2 + 𝑗 − 𝐿𝐵𝐶 − (𝑈𝐵 𝑅 − 𝑖 × 𝑘

Diagonal Matrix

A[i][i] = base address + (i − LBR) × k

𝑨 for Tri-Diagonal Matrix

𝑖 𝑗 = 𝑏𝑎𝑠𝑒 𝑎𝑑𝑑𝑟𝑒𝑠𝑠 + 𝑖 − 𝐿𝐵𝑅 − 1 × 3 + 2 + (𝑗 − 𝑖 + 1) × 𝑘

Abstract Data Type (ADT)

Abstract data type is a way of separating the implementation of a data structure, from its usage.

Abstract Data Type

Is a way of separating the implementation of a data structure from its usage.

Abstract Data Type

Members include member data and member functions. Access specifiers include private and public.

Abstract Data Type Advantages

Client uses ADT without knowing internal implementation details. Implementer can update the ADT without affecting the client program.

Non-primitive Data Structures

Array, Linked List, Stack and Queues, Tree/Binary tree, Hash, Graph

Compile Time Array Creation

Static memory allocation

Run Time Array Creation

Dynamic memory allocation

Benefits of Using Abstract Data Types

Data Hiding, Inheritance and Encapsulation

Formula to Determine Size of 2D Arrays

Number of Columns x Number of Rows

Formula to Determine Size of 3D Arrays

Number of Plates x Number of Columns x Number of Rows

Arrays are generally _, as datatypes are the same.

Homogenous

Data Structures may be classified as _

Heterogenous or Homogenous

Arrays are since their data elements are of the same type.

Homogenous

Arrays are considered a data structure

Linear

Data Structures are classified as

Linear or Non-Linear

Function is uses to create Dynamic Arrays in C.

malloc()

Two main methods of allocating arrays in C

Compile and Run Time

Different Array Operations

Insert, Delete, Search, Display/Traversal, Create, Update

Array Search - Best Case Time Complexity

0(1)

Array Search - Avverage Case Time Complexity

0(n)

Main Purpose of an Array Search Function

Check if Element is Present and if Not Present

Condition for Insertion into Array

i >= 0

Different Steps of Array Insertion Algorithm

Free the index, Store Element, Update the # of Elements

Best Case Insertion Scenario Represents a _ Time Complexity

Constant

Last Step of Array Deletion Algorithm

Reduce UB by One -- UB = UB - 1

Number of Movements of Array Elements in Worst-Case Deletion Scenario

n-1 Elements Involved

Matrix of Relatively High Proportion of Zero Elements

Sparse Matrix

Two Ways to Represent and Store a Sparse Matrix in Memory

Store All Elements Including Zeroes or store only non-zero elements