Module 9 - Chi-squares

Single sample t-test

Sample relative to reference value

Paired t-test

Two measurements per sampling unit

Two-sample t-test

Compare the means of two groups

One-tailed test

Hypotheses have a level of directionality to them. Only one alpha level for the sample mean to be compared against, all alpha is on one tail, thus a greater chance of rejecting the null hypothesis if our p-value is on that side.

Expected contingency table

The contingency table of expected frequencies under the null hypothesis. Always given as counts. The sum of all counts must be the same as the sum of the counts in the observed contingency table. Typically has fractional values even when the observed does not because it represents the average from a statistical population

One-way expected contingency tables

Main question is to ask whether there are differences in counts among the levels of the variable. All cells have the same expected frequency on an expected contingency table

Two-way expected contingency tables

Researchers are interested in whether the counts across the levels of one variable change differently depending on what level of the other variable is being looked at — the interaction between variables. If there is no interaction, variables are independent (have the same relative proportion across levels of variables) of each other.

Calculating a marginal distribution in a 2-way table

Calculate the marginal distributions (add the row/column to get the count) as proportions (divide by total table count).

Using the marginal distribution, calculate the product of the row and column proportions for each cell multiplied by the total table count.

Chi-squared score (X²)

Measures the distance between the observed and expected contingency tables. Calculates the squared difference on a cell-by-cell basis. (Squared because the importance is in the difference, not which is larger)

Steps to calculate a chi-squared score

1. Take the difference between each observed and expected cell

2. Square the difference

3. Divide by the expected value

4. Sum over all cells in the table

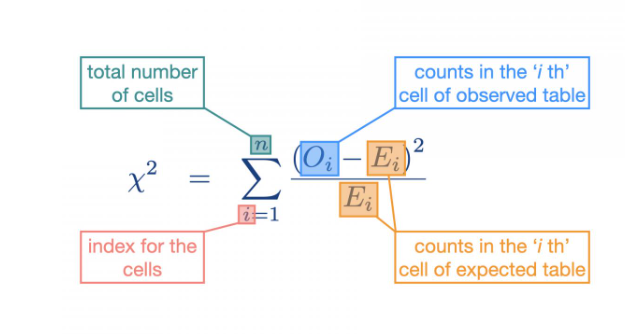
The image represents

Chi-squared score calculation. The sum across all cells ((subtraction of observed from expected)², divided by expected). Same for both 1-way and 2-way contingency tables

Null distribution for a chi-squared test

Sampling distribution of the chi-squared test (which is already a measure of the distance between sample data and the null hypothesis). distribution of chi-square scores you would get from sampling an imaginary statistical population where the null hypothesis was true

Values on the chi-squared distribution

The area under the curve sums to one, can calculate probabilities or quartiles over specific intervals. Different shape because only positive values are possible. Describes the likely variation in chi-squared scores that are due to sampling error alone

Degrees of freedom in a chi-squared distribution

Depends on the number of cells in the expected contingency table. Determines the shape of the chi-squared distribution.

• for 1-way tables, df are number of cells (k) minus 1 (df=k-1)

• for 2-way tables, df are the number of rows minus one multiplied by the number of columns minus 1 (df=(c-1)(r-1))

Becomes flatter with more degrees of freedom.

Steps for a chi-squared test

1. define the null and alternative hypotheses

2. establish the null distribution

3. conduct the statistical test

4. draw scientific conclusions

Hypothesis test for a chi-square test

Locating the critical X² score that corresponds to the Type I error rate on a chi-squared distribution, then comparing it to the observed X² score. The statistical decision can be made by either comparing the observed and critical X² scores, or comparing the p-value and Type I error rate. Always directional (right hand side)

Rejecting the null hypothesis on a chi-squared test

if the observed score is greater than the critical score (i.e., ꭓ²_O>ꭓ²_C) or if the p-value is smaller than the Type I error rate (i.e., p<⍺). On the distribution, if the observed X² is to the right of the line

Failing to reject the null hypothesis on a chi-squared test

If the observed score is less than or equal to the critical score (i.e., ꭓ²_O≤ꭓ²_C) or if the p-value is larger or equal to the Type I error rate (i.e., p≥⍺). On the distribution, if the observed X² is to the left of the line

Scientific conclusions for 1-way tables

• Reject the null hypothesis and conclude that there is evidence to support that the counts are not equal among cells.

• Fail to reject the null hypothesis and conclude that there is no evidence to support that the counts are not equal among cells.

Scientific conclusions for 2-way tables

• Reject the null hypothesis and conclude that there is evidence to support that the variables are not independent of each other.

• Fail to reject the null hypothesis and conclude that there is no evidence to support that the variables are not independent of each other.

Reporting for a chi-square test should include

1. Short name of the test (i.e., ꭓ2)

2. Degrees of freedom

3. Total count in the observed table

4. The observed chi-squared value (two decimal places)

5. p-value (three decimal places)