Lecture 3: Descriptive and Graphing

Levels of Measurement (LoM)

• Nominal

• Ordinal

• Interval

• Ratio

Characteristics of Nominal Variables

• Attributes are named.

Characteristics of Ordinal Variables

• Attributes are named.

• Attributes can be ordered.

Characteristics of Interval Variables

• Attributes are named.

• Attributes can be ordered.

• Distance is meaningful.

Characteristics of Ratio Variables

• Attributes are named.

• Attributes can be ordered.

• Distance is meaningful.

• Absolute zero.

Descriptive statistics

Describing the data.

Inferential statistics

Making inferences about the population based on the sample.

Parametric statistics

Estimate the parameters of a population, based on the normal distributions.

Includes: mean, standard deviation, skewness, kurtosis.

Non-parametric statistics

Do not assume sampling from a population which is normally distributed.

Includes median, frequencies.

Characteristics of Parametric statistics

• More powerful - more sensitive

• More assumptions - normal distribution

• Vulnerable to violations of assumptions - less robust

Non-parametric statistics

• Less powerful - less sensitive

• Fewer assumptions - do not assume a normal distribution

• Less vulnerable to assumption violations - more robust

Central tendency

Statistics which represent the ‘centre’ of a frequency distribution. Includes mode, median, and mean.

LoM and Central Tendency

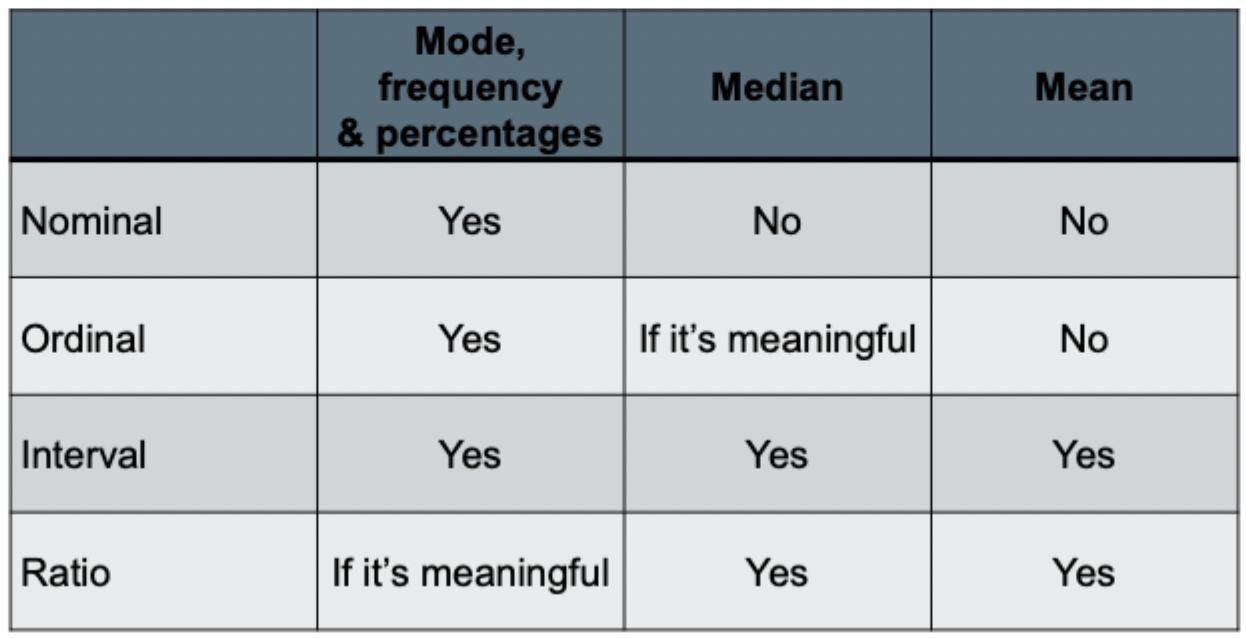
Mode (Mo)

The most common/frequent score; the highest point in a frequency distribution, the most common response.

Frequencies (f) and percentages (%)

The number of responses in each category, and the percentage of responses in each category.

Median (Mdn)

The mid-point of the distribution; Quartile 2, 50th percentile.

Mean

The average score.

Distribution

Measures the shape, spread, and dispersion of your data, as well as the deviation from the central tendency.

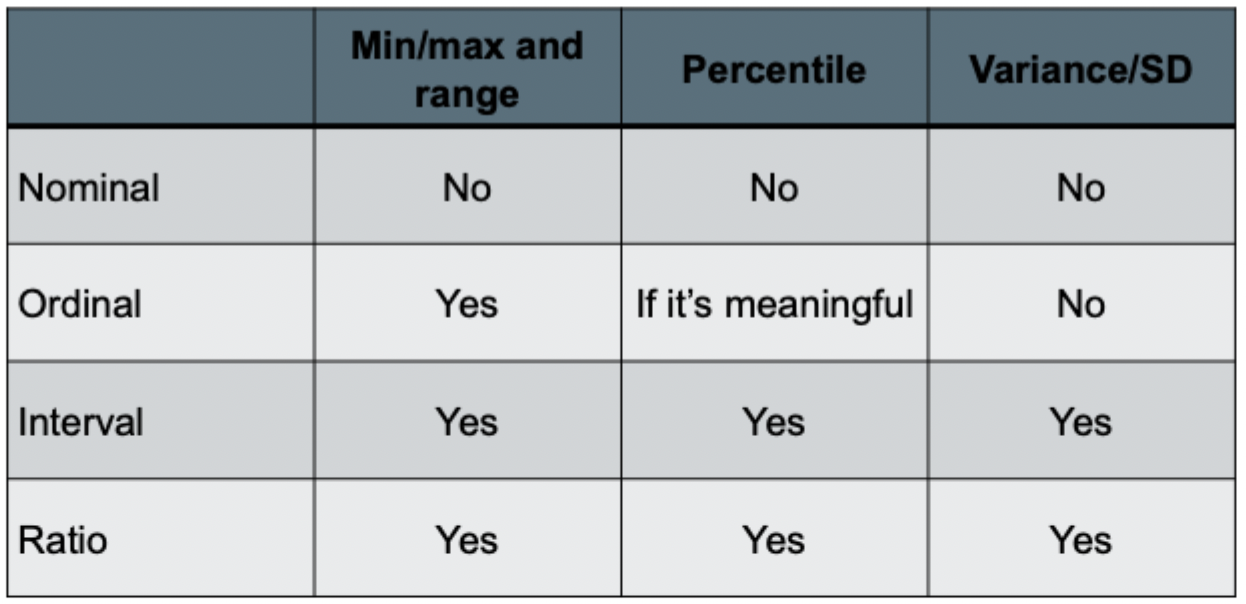
Which statistics can you use for non-parametric stats?

• Minimum and maximum

• Range

  • Percentiles

Which statistics can you use for parametric stats?

• Standard deviation

• Skewness

• Kurtosis

LoM and Distribution 

Variance

The average squared distance from the mean.

Variance Formula

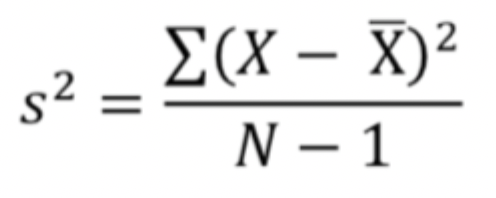
Standard Deviation (SD)

The square root of the variance.

Standard Deviation (SD) Formula

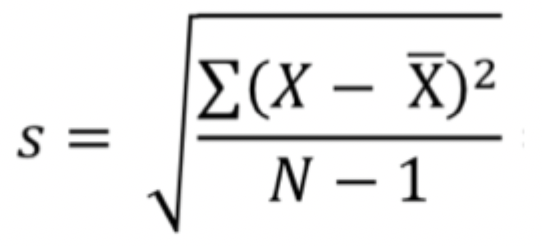
Descriptives for Nominal Data

• Which is the most frequent? (similar to the mode)

• Which is least frequent?

• What are the frequencies?

• Cumulative percentages

• Ratios

Descriptives for Ordinal Data

• Which is the most frequent? (similar to the mode)

• Which is least frequent?

• What are the frequencies?

• Cumulative percentages

• Ratios

• Percentiles

Descriptive for Interval Data

• Central tendency - mode, median, mean.

• Shape/spread - minimum, maximum, range, standard deviation, skewness, kurtosis.

Descriptives for Ratio Data

• Central tendency - mode, median, mean.

• Shape/spread - minimum, maximum, range, standard deviation, skewness, kurtosis.

• Ratios

What can you use to describe central tendency?

• Frequencies

• Percentages

• Mode

• Median

• Mean

What can you use to describe the distribution?

• Minimum and maximum values

• Range

• Quartiles

• Standard deviation

• Variance

Four Components of a Normal Distribution

• Mean

• Standard deviation

• Kurtosis

• Skew (negative or positive)

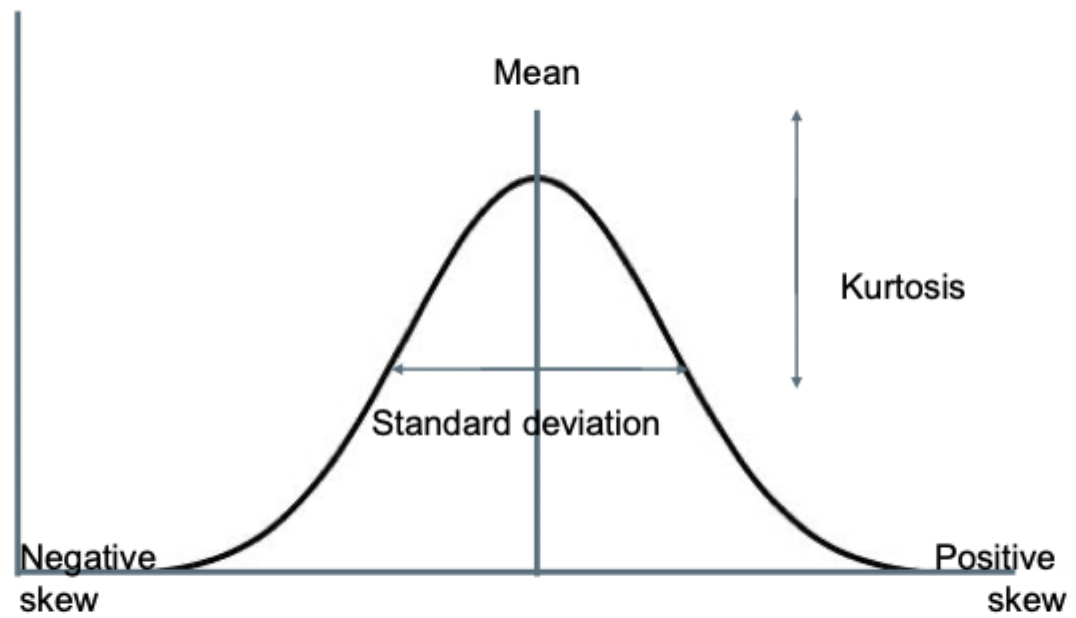
68-95-99.7 Rule

• 68% of the data are within 1 standard deviation of the mean.

• 95% of the data are within 2 standards deviations of the mean.

• 99.7% of the data are within 3 standard deviations of the mean.

Skewness

A measure of the lean of the distribution.

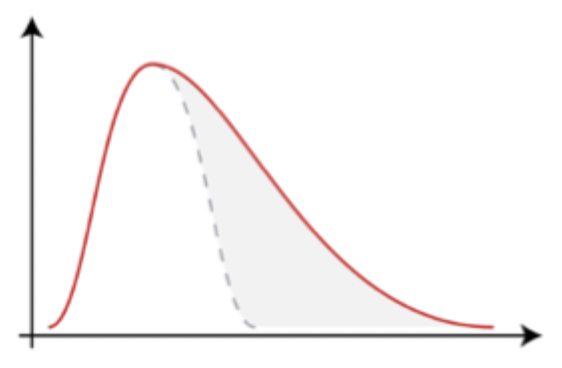
Positive skew

Tail to the right

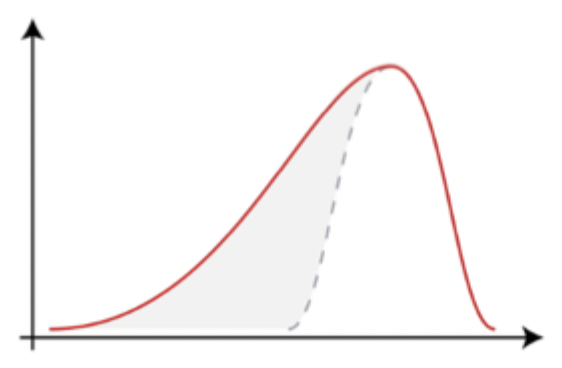
Negative skew

Tail to the left

What causes skew?

• An outlier

• Floor effects

• Ceiling effects

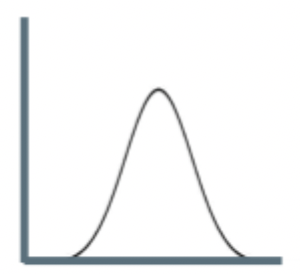
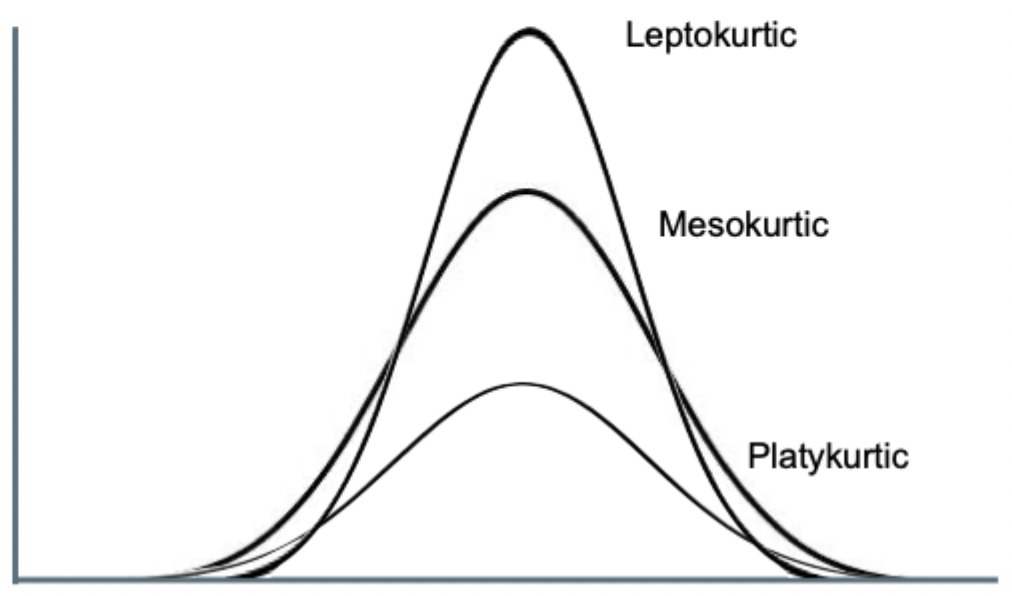
Kurtosis

How flat vs how peaked the distribution of data is.

Positive kurtosis

Peaked data

Negative kurtosis

Flat data

Examples of Kurtosis

• Leptokurtic - narrow, skinny, peaked

• Mesokurtic - moderate

• Platykurtic - flat

Things to look at on non-normal distributions

• How many peaks are there?

  • One peak = unimodal

  • Two peaks = bimodal

  • More than two peaks = multi-modal

• Is there a tail? (skewness)

  • To the right = positive skew

  • To the left = negative skew

• How peaked or flat is it? (kurtosis)

  • Flat = platykurtic

  • Peaked = leptokurtic

How does skew effect measures of central tendency?

• In a normal distribution (symmetrical), the mean = median = mode.

• If there is positive skew, then mode < median < mean.

• If there is negative skew, then mean < median < mode.

Statistics to describe a non-normal distribution

Use non-parametric descriptive statistics:

• Minimum and maximum value

• The range of values (maximum - minimum)

• Percentiles

• Quartiles:

  • Q1

  • Q2 (median)

  • Q3

  • Interquartile ratio (Q3 - Q1)

Steps to take when graphing

1. Ask yourself, what is the purpose of the graph?

2. Select the type of graph to use.

3. Draw and modify graph to be clear, non-distorting, and well-labelled.

Non-parametric (nominal or ordinal) graphs

• Bar graph

• Pie chart

Parametric (normally distributed interval or ratio) graphs

• Histogram

• Stem and leaf plot

• Box plot

Bar chart/bar graph

Pie chart

Histogram

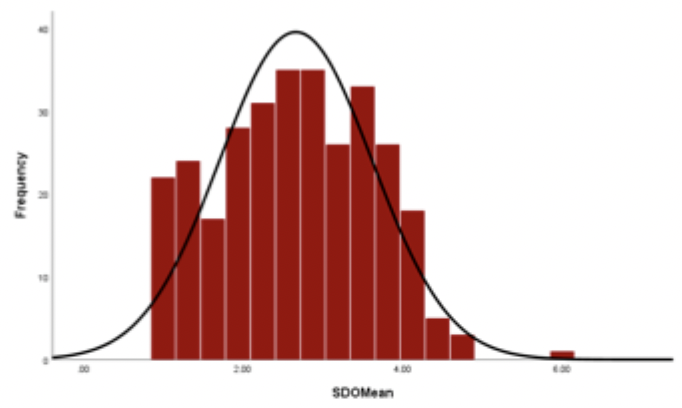
Stem and leaf plots

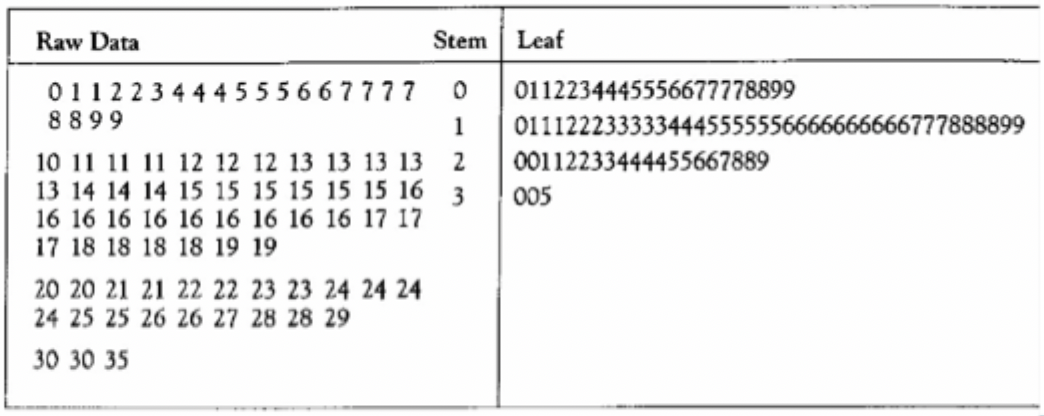
Box plot

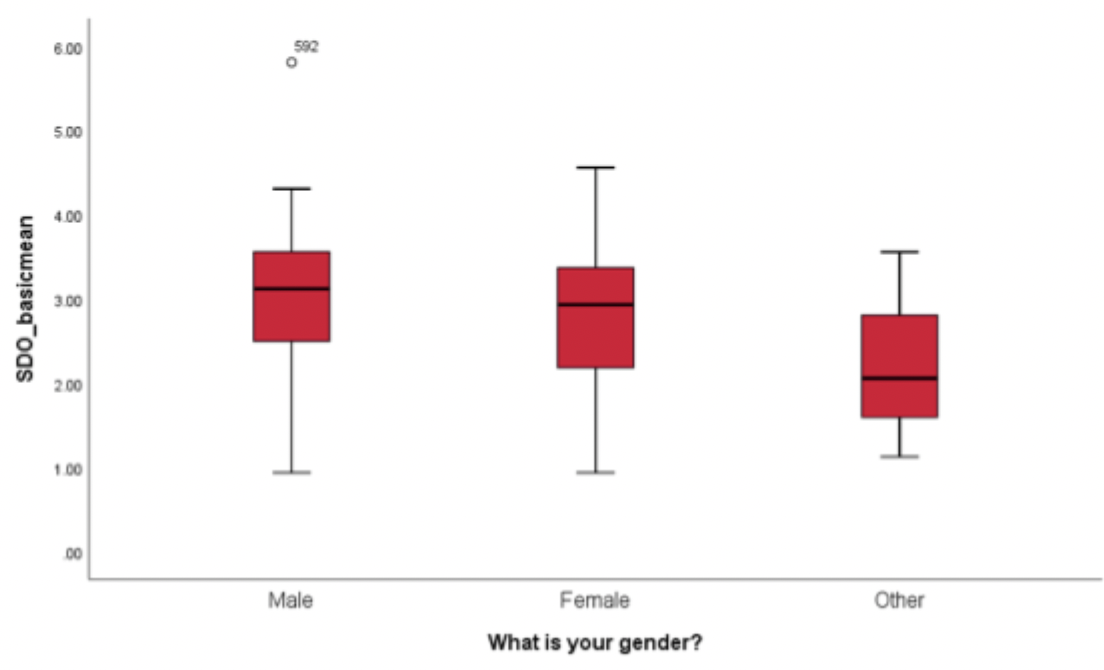
Line graph

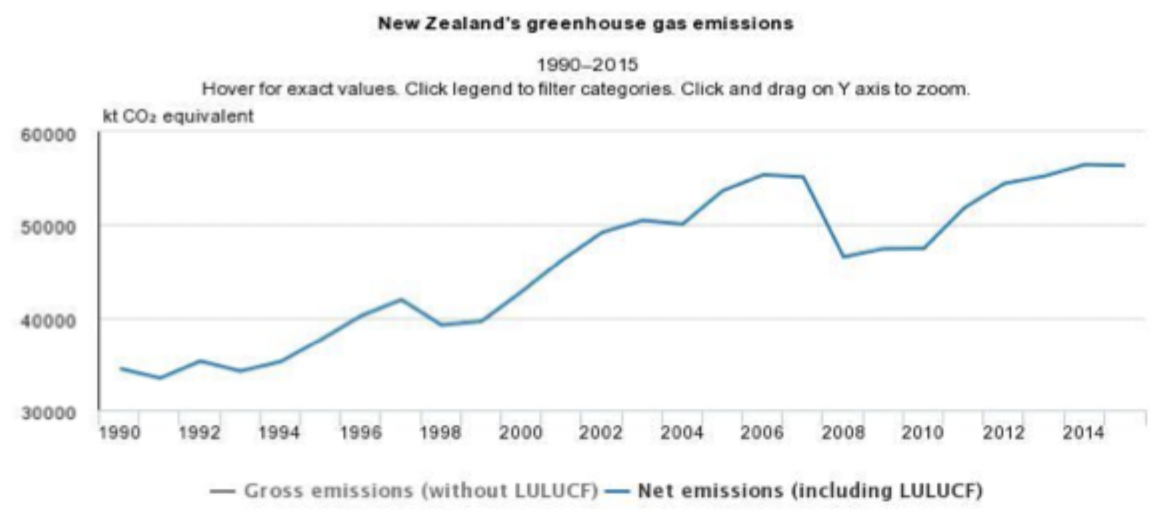
Tufte (1983) on graphical integrity

Misleading graphs

Graphs that:

• Use area of perspective in misleading ways.

• Leave out important context.