7. Electrical properties of excitable cells: Capacitance & Conductance Part 1: Capacitance

Lecture 7

How can we calculate the equilibrium potential of an ion?

• Use the Nernst equation

• It calculates the equilibrium potential (Eion) for any ion in a cell based on concentration gradients

Why do we need the Goldman-Hodgkin-Katz equation instead of just the Nernst equation?

• Most membranes are permeable to multiple ions (Na+, K+, Cl−)

• K+ is usually more permeable than Na+

• GHK equation accounts for multiple permeabilities → gives a more accurate calculation of membrane potential

• If the permeabilities of ions are not provided, you can still estimate the membrane potential using the Nernst equation for each ion.

  1. Calculate the equilibrium potential (Eion) for each ion individually.

  2. Compare the Eion values:

     • If all equilibrium potentials are equal, the membrane potential is equal to that value.

     • If they differ, the membrane potential will lie somewhere within the range of the calculated equilibrium potentials.

Why study electrical properties of excitable cells?

• Helps us understand:

  • How fast membrane potential changes when permeability changes

  • Magnitude of Na+, K+, Cl− currents

• Ion currents act like circuits → create signals in nerve cells

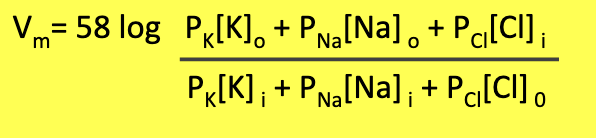
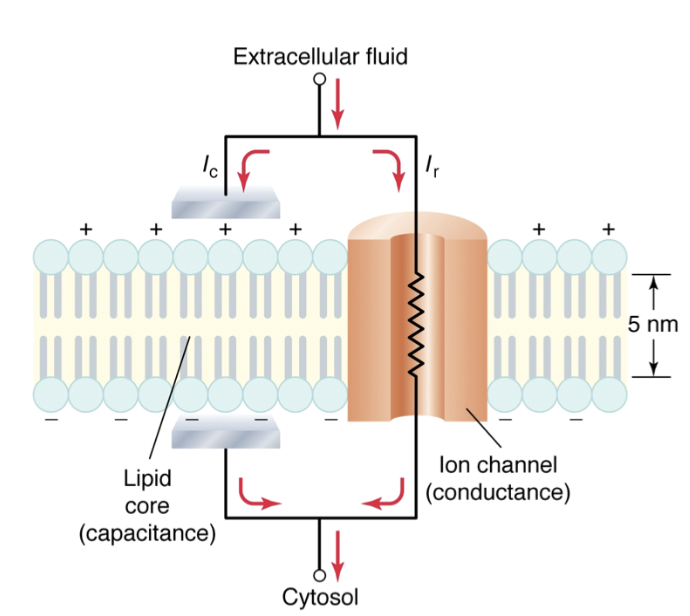
Why does the membrane act as a capacitor?

• Lipid bilayer = insulator (blocks ion diffusion)

• ECF (+ charge) & ICF (- charge)= good conductors

• Insulator between two conductors → forms an electrical capacitor (stores separated charge)

  • Thus, membrane has capacity to hold charge

• Ion channels = conductance pathways

How do we calculate capacitance of a membrane?

• Formula: C = q/V

  • q = electric charge in coulombs stored across the capacitor 

  • V = difference in electrical potential

• Rearranged: q = CV (identify amount of charge stored across a capacitor)

• 1 Farad stores 1 Coulomb per 1 Volt

• Biological membranes: C_m = 10⁻⁶ F/cm²

What is the capacitance of a cell with diameter 10 μm?

1. Main Equation: C_cell = C_m x A_cell

2. Assume Cells are Spherical:

   • Area of sphere: 4πr² or πd² = 314 μm² = Area of cell

   • Convert μm² → cm² 

   • 1 cm = 10 000 μm → 1 cm² = 10⁸ μm²

   • 314 μm² ÷ 10⁸ = 3.14 × 10⁻⁶ cm²

3. Plug into Equation: 

   • C_cell = (10⁻⁶ F/cm²) × (3.14 × 10⁻⁶ cm²) = 3.14 × 10⁻¹² F or = 3.14 pF

   • C_m = 10⁻⁶ F/cm² → biological membrane

How do we start calculating charge across a 50 μm glial cell at Vm = −90 mV? (Part 1)

Given E_k=V_m=-90mV; [K⁺]_o=3mM and [K⁺]_i=108mM

Membrane potential = Equilibrium potential

1. What do we know?

   • Use q = CV to solve for charge (in Coloumbs)

   • C_m = 10⁻⁶ F/cm²

   • V_m=-90mV

2. What we don’t know?

   • Area of the cell

   • Total capacitance of this cell

   • Charge = q

3. Area of cell: A_cell = 4πr² = 4π(25 μm)² = 7854 μm²

   • Convert: 7854 μm² ÷ 10⁸ = 7.854 × 10⁻⁵ cm²

How much charge must be separated in a 50 μm glial cell at Vm = −90 mV? (Part 2)

4. Total Capacitance of the Cell: C_cell = C_m x A_cell

   • (10⁻⁶ F/cm²)(7.854 × 10⁻⁵ cm²) = 7.854 × 10⁻¹¹ F or 7.854 × 10⁻¹¹ Coloumbs/V

   • Next steps: Find capacitance, then use q = CV

5. Find Charge: q = CV

   • = (7.854 × 10⁻¹¹ Coloumbs / V)(0.090 V)

   • q = 7.069 × 10⁻¹² C

   • Answer: 7.069 pC

How can we determine how many ions move to establish a membrane potential, and does it significantly change ion concentration?

• Calculating charge separated (q) does not directly tell us how many ions moved.

• For glial cells, Vm = EK → only K+ moves.

• Convert charge to moles of K+ using Faraday’s constant:

  • q = 7.069 × 10⁻¹² C

  • 1 mole of a monovalent ion = 96,485 C

  • Moles K+ moved = 7.069 × 10⁻¹² ÷ 96,485 = 7.326 × 10⁻¹⁷ mol

• Convert moles to ions using Avogadro’s number:

  • 7.326 × 10⁻¹⁷ × 6.022 × 10²³ = 4.4 × 10⁷ K+ ions

• Effect on [K+]: Very small → negligible impact on overall ion concentration

Does the movement of K+ to establish Vm significantly change K+ concentration in glial cells?

• K+ moved to establish Vm = 7.326 × 10⁻¹⁷ mol

• Step 1: Calculate total K+ initially in cell

  • Intracellular [K+] = 108 mM = 0.108 mol/L

  • Cell volume = sphere: 4/3 π r³ = 4/3 π (25 μm)³ = 65,550 μm³

  • Convert to liters: 65,550 μm³ ÷ 10¹⁵ = 6.555 × 10⁻¹¹ L

• Total K+ initially: 0.108 mol/L × 6.555 × 10⁻¹¹ L = 7.079 × 10⁻¹² mol

• Compare to K+ moved: 7.326 × 10⁻¹⁷ mol → very small fraction → negligible effect on [K+]

Note:
1 mL = 1 cm³

What % of K+ ions leave glial cells to establish Vm = −90 mV, and what does this mean in practical terms?

• % moved = (7.326 × 10⁻¹⁷ mol ÷ 7.079 × 10⁻¹² mol) × 100

• = 0.001%

• Meaning: For every 1,000,000 K+ ions, only ~10 ions move to establish Vm = EK = −90 mV

• Conclusion: Ion movement for Vm does not significantly change [K+] inside the cell