Biostatistics exam 3 - Comparing Two Means

Different study designs for comparing two means

1. Two sample design

- two groups

- each group composed of independent sample of units (a sample in one group has no connection with individuals in the same group or other group)

2. Paired design

- two groups

- each sample unit receives both treatments

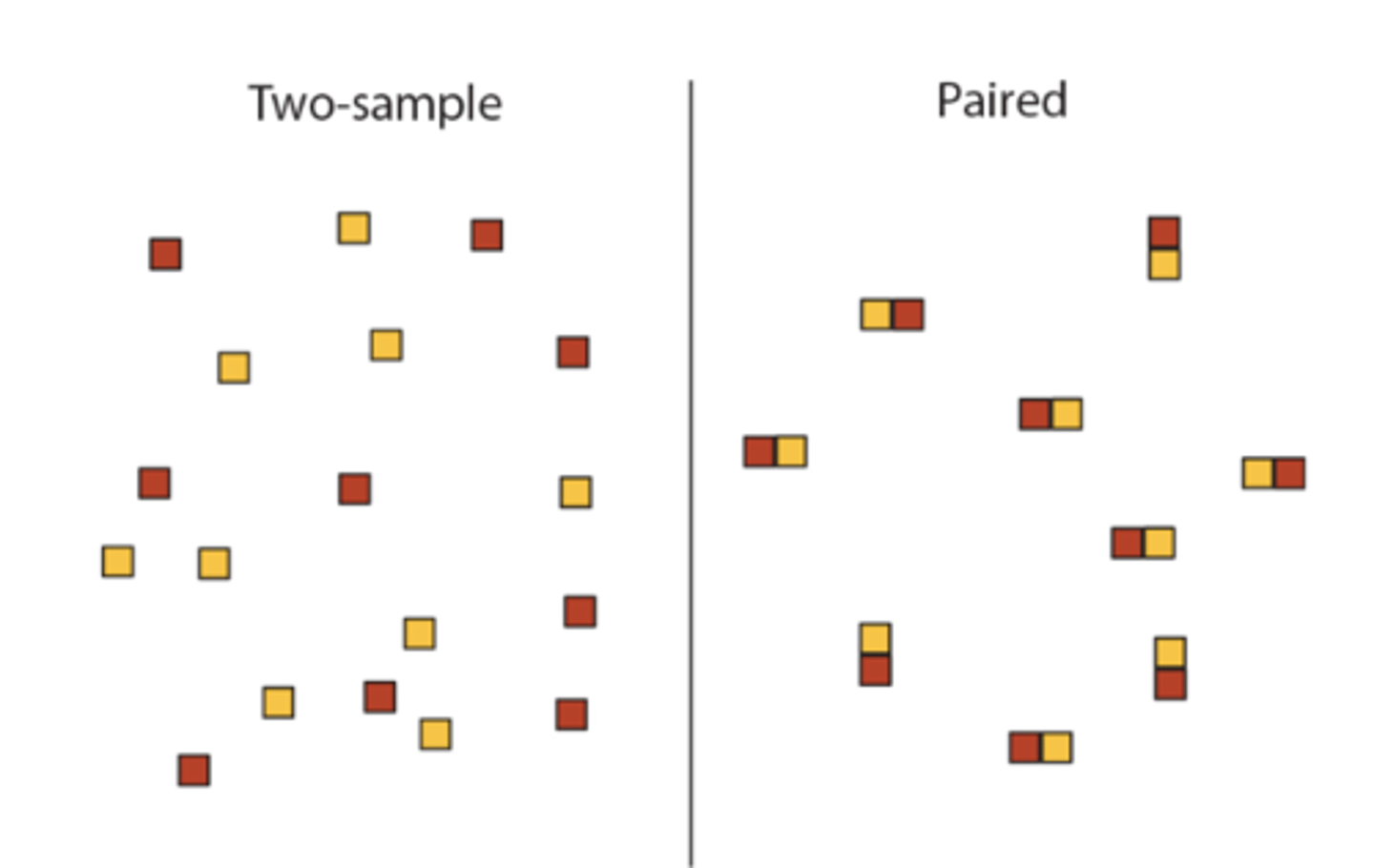
Paired design

Both treatments are applied to every sample unit

• paired designs are usually more powerful than a two-sample design

- control for variation among sampling units

- if you have the same sample units, you have the same spread

- two-sample → have two different spreads

• paired measurements are converted to a single measurement by taking the difference between them

- if there is no interaction, you expect the difference between the two measurements to be zero (mean difs should be 0)

two-sample design

Each treatment group is composed of an independent, random sample of units

• you have two different spreads

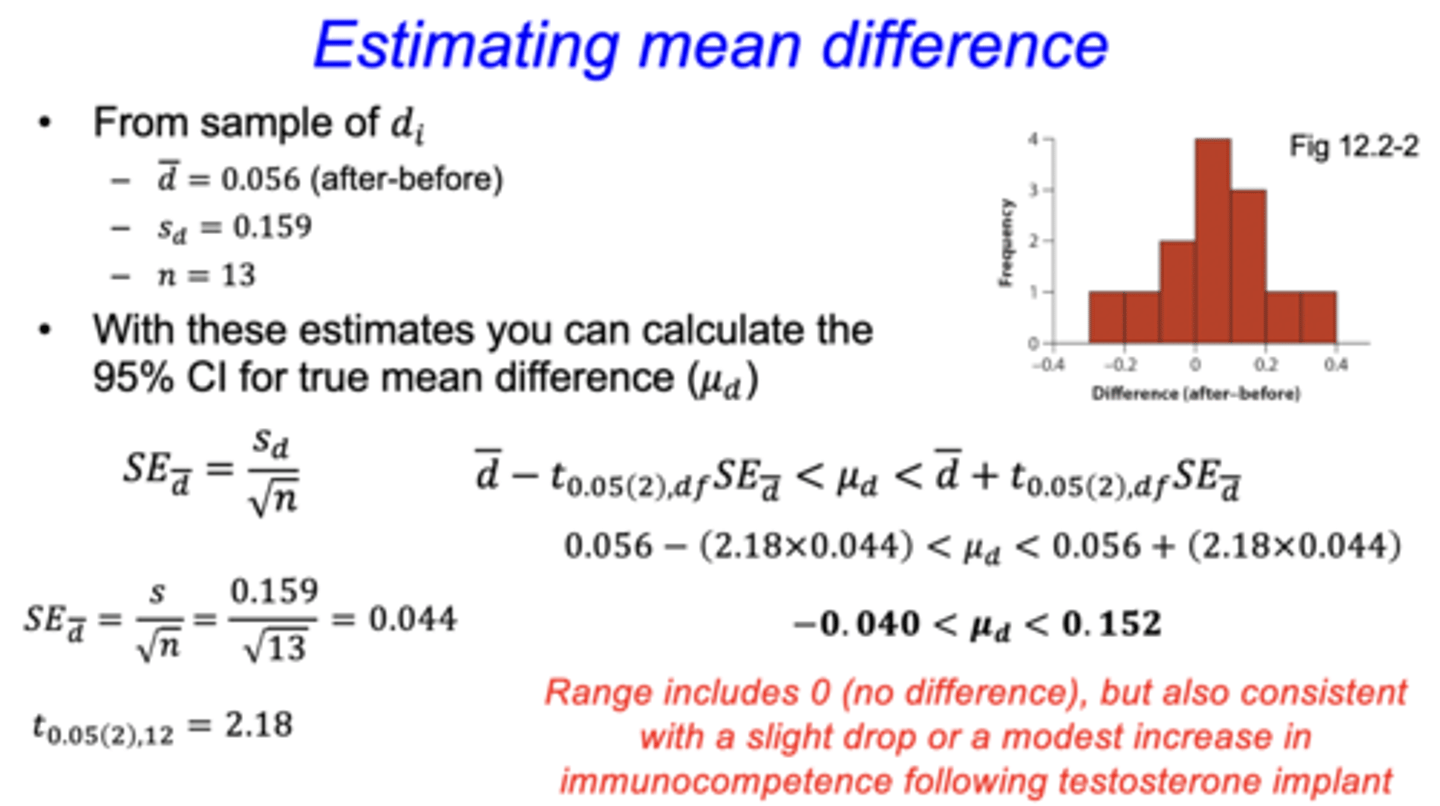
how to calculate the 95% confidence interval for the true mean of difference (µd) - paired design

d bar = mean of differences (i.e. after-before)

Sd = standard deviation of differences

n = sample size

• if the range includes 0, then there is no difference

- in the example, the range is consistent with a slight drop or a modest increase

Paired t-test

Used to test the null hypothesis that the mean difference of paired measurements equals a specific value

Paired t-test hypotheses

H₀: mean change in antibody production after testosterone implants was 0 (µd = 0)

Ha: mean change in antibody production after testosterone was not zero (µd ≠ 0)

*NOTE: some studies could do a ratio (A/B)

- if the study uses a ratio H₀=1

Paired t-test test statistic

when paired samples are reduced to a single measurement (d), the calculation of test statistic is the same as a one sample t-test

how do you determine p-value with a paired t-test?

1. with a computer

2. with a statistical table

Assumptions of paired t-test

1. sampling units are randomly sampled from the population

2. paired differences have a normal distribution in the population

Hypotheses for formal tests of normality

H₀: sample has normal distribution

Ha: sample does not have normal distribution

Why should formal tests of normality be used with caution?

1. small sample sizes lack power to reject a false null (Type II error)

2. large sample sizes can reject null when the departure from normality is minimal and would not affect methods that assume normality

Shapiro-Wilk test

evaluates the goodness-of-fit of a normal distribution to a set of data randomly sampled from a population

• most commonly used formal test of normality

•estimates mean and standard deviation using sample data

• tests goodness of fit between sample data and normal distribution (with the mean and standard deviation of the sample)

• p-val > 0.05 (normal/fail to reject), p-val<0.05 (reject normality)

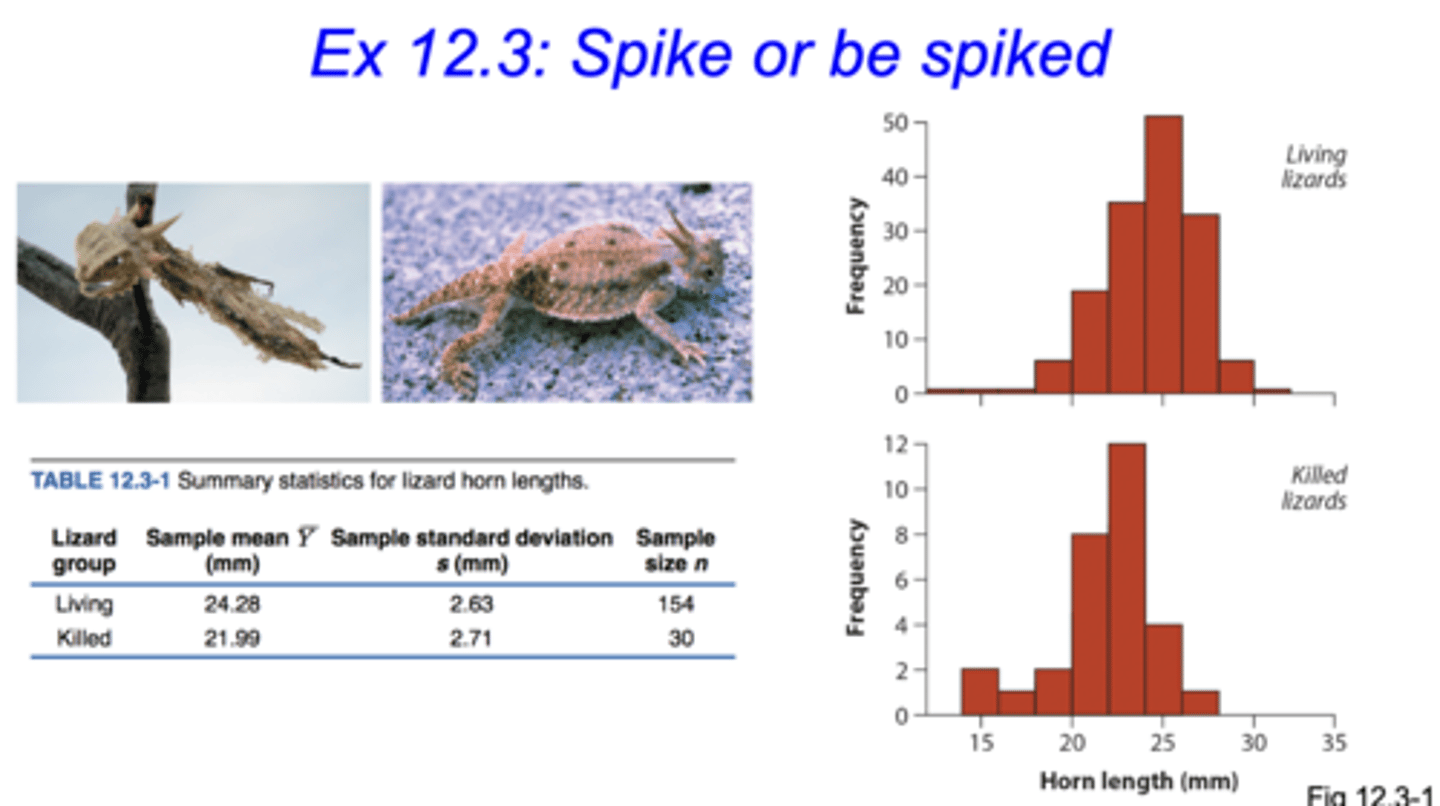
what type of graph should you use in a two sample design?

stacked histograms with the same x-axis

The two ways to analyze a two sample design

1. 95% confidence interval

2. two sample t-test

95% confidence interval for difference between two means (two sample design)

Statistic of Interest: Y₁bar - Y₂bar

• if there is no difference between means Y₁bar - Y₂bar = 0

•you need to take into account the pooled sample variance

degrees of freedom for a 95% confidence interval of diff between two means

df = N - 2

df = df₁ + df₂

df₁ = n-1

df₂ = n-1

calculating standard error of Y₁bar - Y₂bar

pooled sample variance Sp^2

The average of the variances of the samples weighted by their degrees of freedom

* NOTE: S=sd, V=S²

equation for pooled sample variance Sp^2

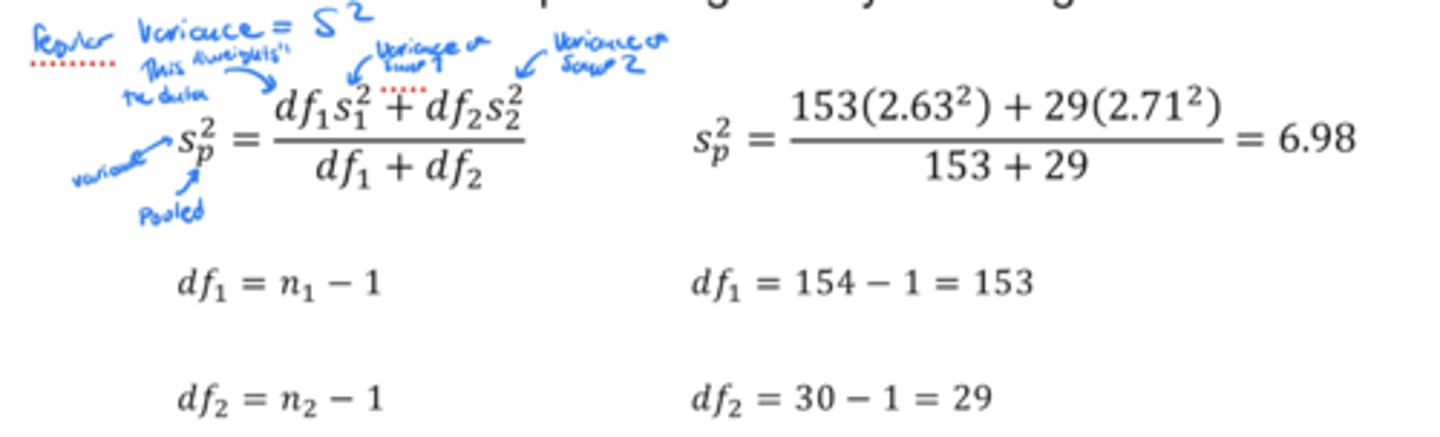
two sample t-test

Simplest test to compare the means of a numerical variable between two independent groups (usually means)

Hypotheses of a two sample t-test

H₀: µ₁ = µ₂

Ha: µ₁ ≠ µ₂

test statistic of a two sample t-test

t-value (diff equation!)

assumptions of a two sample t-test

1. each of the two samples is a random sample from its population

2. numerical variable is normally distributed in each population

- robust to minor deviations from normality

- need to run Shapiro Wilk test on both samples

3. standard deviation and variance of the numerical variable is the same in both populations (equal spread)

- robust to some deviation from this if sample sizes of two groups are approximately equal

- tested with Levine's test

formal tests of equal variance

• an F-test is sometimes used, but is highly sensitive to departures from the assumption that the measurements are normally distributed in the population

• Levine's test performs better and is recommended

hypotheses of Levine's test

H₀: variances of the two groups are equal

Ha: variances of the two groups are not equal

• NOTE: can be extended to more than two groups

what if variances in two groups are not equal?

• standard t=test works well if both sample sizes are greater than 30 and there is less than 3-fold difference in standard deviations (we and ignore Levene's test)

• Use a Welch's t-test

Welch's t-test

Compares the means of two groups and can be used even when the variances of the two groups are not equal

• slightly less power compared to standard t-test

correct sampling units

When comparing the means of two groups and] assumption is that the samples being analyzed are random samples (individuals have an equal probability and independent chance of being sampled)

• often repeated measurements are taken on each sampling unit

- this makes the identification of independent units more challenging

correct sampling units - salmon in the stream example

• individual salmon are not a random sample

• grouped by stream

• stream is the independently sampled unit

• salmon within streams should be summarized by single measurement

- proportion surviving

•NOTE: if you treated the salmon as the sampling unit:

- these samples are not independent because they are caught in the same stream

- you are inflating n to get a significant P

fallacy of indirect comparison

Comparisons between two groups should always be made directly, not indirectly by comparing both to the same hypothesized value

• common error: compare each group mean to hypothesized Value rather than comparing group means to each other

• ex: since group 1 is significantly different then zero, but group 2 is not, then groups 1 and 2 are significantly different from each other

- PROB: you never actually compared the two groups to each other

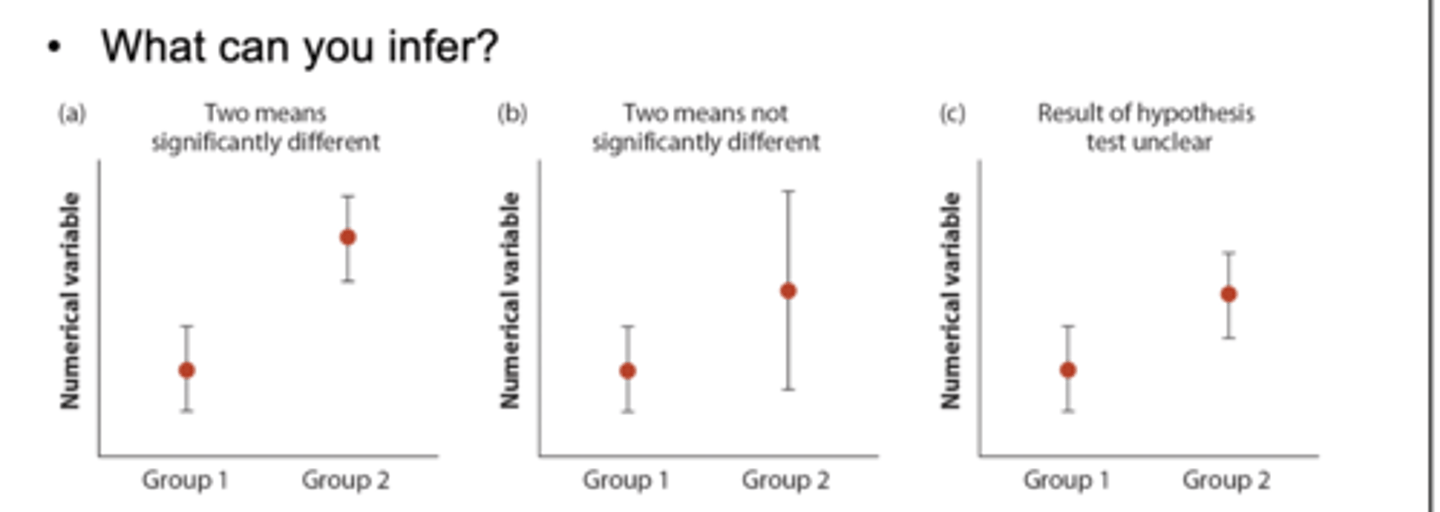
interpreting overlap in confidence intervals

1. two means significantly different: 95% CI don't overlap

2. two means not significantly different: 95% CI overlap and at least one error bar overlaps with a mean

3. results of hypothesis test unclear: error bars overlap but doesn't include me of a group