Chapter 8. Storage and Indexing

Where does a DBMS store persistent data?

A DBMS stores vast quantities of data, and the data must persist across program executions. Therefore, data is stored on external storage devices such as disks and tapes, and fetched into main memory as needed for processing.

Disks are the most important external storage devices. They retrieve any page at a fixed cost per page.

Tapes are sequential access devices and force us to read data one page after the other.

How does a DBMS bring data into main memory for processing?

Data is fetched into main memory as needed for processing.

Data is read into memory for processing, and written to disk for persistent storage, by a layer of software called the buffer manager. When the files and access methods layer (which we often refer to as just the file layer) needs to process a page, it asks the buffer manager to fetch the page, specifying the page's rid. The buffer manager fetches the page from disk if it is not already in memory.

What DBMS component reads and writes data from main memory, and what is the unit of I/O?

The unit of information read from or written to disk is a page. The size of a page is a DBMS parameter, and typical values are 4KB or 8KB.

The buffer manager fetches the page from disk if it is not already in memory.

Why does a DBMS store data on external storage?

A DBMS stores data on external storage because the quantity of data is vast, and must persist across program executions.

Define the term 'page' in the context of DBMS. Why is it considered the unit of information read from or written to disk?

A page in DBMS is the unit of information that is read from or written to the disk. The size of page is typically 4KB or 8KB.

Why are I/O costs important in a DBMS?

I/O costs are of primary important to a DBMS because these costs typically dominate the time it takes to run most database operations. Optimizing the amount of I/O’s for an operation can result in a substantial increase in speed in the time it takes to run that operation.

What is a record ID? Given a records’s id, how many I/Os needed to fetch it into main memory?

A record id is a unique identifier for a particular record in a set of records.

A rid has the property that we can identify the disk address of the page containing the record by using the rid. The number of I/O’s required to read a record, given a rid, is therefore 1 I/O.

What is the role of the buffer manager in a DBMS?

The buffer manager reads data from persistent storage into memory as well as writes data from memory into persistent storage.

What is the role of the disk space manager?

The disk space manager manages the available physical storage space of data for the DBMS.

How does the buffer manager and disk space manager these layers interact with the file and access methods layer?

When the files and access methods layer needs to process a page, it asks the buffer manager to fetch the page, specifying the page’s rid and put it into memory if it is not all ready in memory.

File and access methods layer when wants to save new data on the disk requests disk space manager to allocate space for the new data. Disk space manager allocates space for the new records from the available space on the external storage device.

The cost of page I/O (input from disk to main memory and output from memory to disk)

Dominates the cost of typical database operations, and database systems are carefully optimized to minimize this cost.

What is a file organization?

File organization is method of arranging a file of records on external storage.

It involves how records are physically stored on disk and how memory is utilized.

The simplest form of file organization is an unordered file or heap file, where records are stored in random order across the pages of the file.

What is an index?

Index is a data structure which stores information about records stored in a database, this information is used for faster retrieval of the data records thus reducing the amount of time required to search keys for a record.

Without index DBMS has to perform a scan operation to identify the record matching the condition in the query, which takes large amount of time and thus increasing the cost and performance degradation of the DBMS.

What is search key?

A search key is the fields stored in an index by using which one can effectively search the records requested in a query.

Why do we need indexes?

Without index DBMS has to perform a scan operation to identify the record matching the condition in the query, which takes large amount of time and thus increasing the cost and performance degradation of the DBMS.

What is the relationship between files and indexes?

Files and indexes are closely related in that an index is built on top of a file to improve the performance of data retrieval operations. While a file contains the actual data records, an index helps in quickly locating these records by maintaining additional structures (like tress or hash tables) that facilities efficient searches. he index typically contains search keys and pointers to the locations of the records in the file.

Can we have several indexes on a single file of records?

Yes, we can have several indexes on a single file of records. Multiple indexes can be created on different search key fields to support various types of queries and optimize retrieval operations. For example, an employee records file can have one index based on salary and another based on age to efficiently handle queries involving these attributes.

Can an index itself store data records (i.e. act as a file)?

Yes, an index can store data records and act as a file. There are three main alternatives for what to store as a data entry in an index:

1. The data entry k* is the actual data record with the search key value.

2. The data entry is a (k, rid) pair of the search key and the record ID (RID) of the data record.

3. The data entry is a (k, rid-list) pair of the search key and a list of record IDs (RID-list) of data records with the given search key value.

Heap File

Files containing an unsorted set of records that are uniquely identified by a record id which allows them to be inserted or deleted using that id.

What is an index?

It is a performance tuning method of allowing faster retrieval of records from the table. An index creates an entry for each value and it allows us to efficiently retrieve all records that satisfy search conditions on the search key fields of the index.

We can also create additional indexes on a given collection of data records, each with a different search key, to speed up search operations that are not efficiently supported by the file organization used to store the data records

What is data entry in an index?

It refers to the records stored in an index file

A data entry with search key value k, denoted as k*, contains enough information to locate (one or more) data records with search key value k. We can efficiently search an index to find the desired data entries, and then use these to obtain data records (if these are distinct from data entries).

What operations are supported by the file of records abstraction?

A file of records abstraction is implemented by file and access methods layer in DBMS, it can perform the following operations

• It can create a file

• Delete a file

• It can create a record insert the record

• delete a record

• scan operation: means scanning of all the records in a file one at a time.

What is the difference between a primary index and a secondary index?

Primary index: An index is created on different set of columns in a table, if the index includes the primary key column such an index is called as primary index.

• Primary index does not have duplicate values

• A primary index typically uses alternative (1) for data entries where each data entry k* is the actual data record with the search key value k.

• Example: In an employee database, if "EmployeeID" is the primary key, a primary index on "EmployeeID" would ensure that each entry in the index is unique and directly maps to a specific record.

Secondary index: An index that does not include the primary key column is called as a secondary index

• Secondary index may have duplicate value.

• The search key value field in an index may have duplicates.

• Secondary indexes use alternatives (2) or (3) for data entries.

• Example: In an employee database, a secondary index on "salary" may have multiple entries with the same salary value, each pointing to different employee records.

What is a duplicate data entry in an index?

An entry in the index is in duplicate when the entry has a search key value same as another entry in the index. That is if two or more entries in the index have same search key values they are said to be duplicates.

What is the difference between a clustered index and an unclustered index?

Clustered index is one where the ordering of data records is the same as or close to the ordering of data entries in the index.

• A file can only have one clustered index because it determines the physical order of the records.

• Making it efficient for range queries

• An index that uses alternative (1) is clustered. Clustered indexes often use Alternatives (2) or (3) for data entries, only if the data records are sorted on the search key field.

Unclustered index: is one where the order of the data records is different from the order of the data entries in the index.

• Multiple unclustered indexes can be created on a single file since they do not affect the physical order of data records.

• Unclustered indexes can use alternatives (2) or (3)

If an index contains data records as data entries can it be unclustered?

No, if an index uses alternative (1), where data entries are actual data records, it cannot be unclustered. This is because, by definition, alternative (1) means that the data records are stored directly in the index, making it a clustered.

In Alternative (1), the index is a file organization in itself, and the data records are stored in the same physical order as the index entries, thus making it clustered.

Consider alternatives (1), (2), (3) for data entries in an index, as discussed in section 8.2. Are all of them suitable for secondary indexes? Explain.

No, index based on alternative (1) is not suitable for secondary index. As alternative (1) contains the data records as data entries and has no duplicate records. That means an index formed using alternative (1) type data entry is a primary index.

• A primary index cannot be used as a secondary index. Therefore Alternative (1) is not suitable for secondary index.

• Alternative (2) and (3) are suitable for secondary indexes.

How is data organized in a hash-based index? When would you use a hash-based index?

In a hash-based index, records are organized into buckets using a hash function. A hash function is applied to the search key of a record to determine the bucket it belongs to. This function converts the search key value to a bucket number.

On inserting a record, the hash function is used to determine the appropriate bucket. The record is then inserted into the primary page of that bucket, with overflow pages allocated as necessary.

Primary

When would you use a hash-based index:

• No need for index entries.

• Primary page in a given bucket can be retrieved in one or two disk I/Os.

• Hashing to quickly find records that have a given search key value. For example, if the file of employee records is hashed on the name field, we can retrieve all records about Joe.

• They are ideal for searches involving unique keys, such as primary keys or candidate keys, where each search key corresponds to exactly one record.

• They handle insert and delete operations efficiently, as the hash function quickly identifies the bucket for a new or existing record.

Limitations:

• Hash-based indexes are not suitable for range queries or ordered data retrieval since the hash function does not preserve the order of the keys.

  • Example: Retrieving all employees with ages between 30 and 40 would be inefficient with a hash-based index.

• If the hash function does not distribute the data uniformly, it can lead to bucket overflow and increased retrieval times.

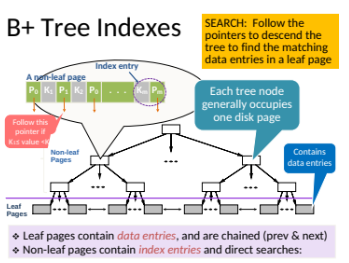
How is data organized in a tree-based index? When would you use a tree-based index?

• The tree is composed of multiple levels: the root, non-leaf nodes and leaf nodes.

• Each node in the tree contains keys and pointers.

• The leaf nodes contains data entries (e.g.,, employee records). The nodes are linked in a doubly-linked list to facilitate range queries and sequential access.

• Non-leaf pages contain index entries; only used to direct searches.

• The tree is balanced meaning that all paths from the root to the leaf nodes are of the same length. This ensures that the height of the tree is minimized, leading to consistent and efficient access times.

• The fan-out of a tree refers to the number of children each non-leaf node can have. A higher fan-out reduces the tree height, improving search efficiency.

  • For example, if the fan-out is 100, a tree with height 4 can handle up to 100 million leaf pages.

When would you use a tree-based index?

• B+ tree index is good for range searches.

• Tree-based indexes maintain in sorted order, making such retrievals efficient.

• Tree-based indexes handle dynamic sets well, supporting efficient insertions and deletions while maintaining the balanced structures.

• Useful for large databases where the index itself might not fit in memory.

Consider a relation stored as a randomly ordered file for which the only index is an unclustered index on a field called sal. If you want to retrieve all records with sal > 20, is using the index always the best alternative? Explain.

No it is not efficient to use index to retrieve data records which satisfy the condition sal>20 when the index is unclustered. Because as the index used is unclustered the logical ordering of the data entries is different from the physical ordering. Each record’s rid satisfying the condition may point to a different page on the disk when an index is used. If the number of records with sal > 20 is larger than the number of blocks, then a full table scan will likely be faster and more efficient due to the lower I/O cost of sequential access.

Consider the following operations: scans, equality and range selections, inserts, and deletes, and the following file organizations: heap files, sorted files, clustered files, heap files with an unclustered tree index on the search key and heap files with an unclusterted hash index. Which file organization is best suited for each operations?

File Scanning (The time complexity is O (1)):- Heap file organization with nonclustered hash index will be suitable to implement file scan operation, as it would be a tedious task to traverse the entire list of files to find a specific file, so we maintain a heap structure mapping each node with the hash Hope index so that we can traverse down the heap directly to get the file.

Range selection (The time complexity is O(log(N)):- Heap file organization with non-clustered tree index on search key can help us to traverse the heap, we have to choose the option to search higher or lower index, this property helps to maintain the range so that we can search until match the desired key. Insertion and deletion (the time complexity is O(log(N)):- Best for sorted file organization as insertion and deletion operations are easier to perform on arrays rather than trees. So in the heap, we have to maintain the heap structure after every insertion/deletion. Sorting an array has no such overhead, we can apply a binary search to find the exact location of the file

What are the main contributions to the cost of database operations? Discuss a simple cost model that reflects this.

A simple cost model for estimating the cost of database operations focuses on the I/O component, as I/O is typically the dominant cost.

• B : # of data pages

• R: # of records per page

• D: average time to read or write a disk page.

• C: average time to process a record

• H: time to apply hash function to a record

• F: fan-out, which is average number of children for non-leaf node (typically at least 100)

Typical value; D = 15 milliseconds

Typical value C and H = 100 nanoseconds

• A sorted file also offers good storage efficiency but insertion and deletion of records is slow. Searches are faster than in heap files. It is worth noting that, in a real DBMS, a file is almost never kept fully sorted.

• A clustered file offers all the advantages of a sorted file and supports inserts and deletes efficiently. Searches are even faster than in sorted files, although a sorted file can be faster when a large number of records are retrieved sequentially because of blocked I/O

• Unclustered tree and hash indexes offer fast searches, insertion, and deletion, but scans and range searches with many matches are slow. Hash indexes are a little faster on equality searches, but they do not support range searches.

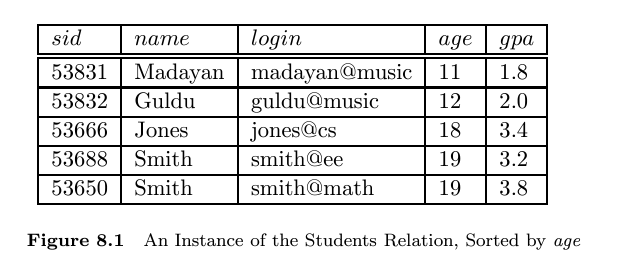
Consider the instance of the Students relation shown in Figure 8.1, sorted by age: For the purposes of this question, assume that these tuples are stored in a sorted file in the order shown; the first tuple is on page 1 the second tuple is also on page 1; and so on. Each page can store up to three data records; so the fourth tuple is on page 2.

Explain what the data entries in each of the following indexes contain. If the order of entries is significant, say so and explain why. If such an index cannot be constructed, say so and explain why.

1. An unclustered index on age using Alternative (1).

2. An unclustered index on age using Alternative (2).

3. An unclustered index on age using Alternative (3).

4. A clustered index on age using Alternative (1).

5. A clustered index on age using Alternative (2).

6. A clustered index on age using Alternative (3).

7. An unclustered index on gpa using Alternative (1).

8. An unclustered index on gpa using Alternative (2).

9. An unclustered index on gpa using Alternative (3).

10. A clustered index on gpa using Alternative (1).

11. A clustered index on gpa using Alternative (2).

12. A clustered index on gpa using Alternative (3).

The answer to each question is given below/For Alternative (2) the notation (A,(B,C)} is used where A is the search key for the entry and (B,C) is the rid for data entry with B being the page number of entry and c being location on page B of entry For alternative (3) the notation is the same but with the possibility of additional rid's listed.

1. An unclustered index on age using Alternative (1).

   1. Contradiction. Cannot build an unclustered index using alternative (1) since the method is inherently clustered.

2. For unclustered index on age using Alternative (2).

   1. Each page can store up to three data records.

   2. Answer: 11, (1,1), 12, (1,2), 18,(1, 3), 19,(2,1), 19, (2,2). The order of entries is not significant.

3. An unclustered index on age using Alternative (3).

   1. Answer: 11, (1,1), 12(1,2), 18,(1,3), (19, (2,1), (2,2)). The order of entries is not significant.

4. A clustered index on age using Alternative (1).

   1. Answer: 11, 12, 18, 19, 19. The order of entries is significant since the order of the entries is the same as the order of data record.

5. A clustered index on age using Alternative (2).

   1. 11, (1,1), 12, (1, 2), 18,(1,3), 19, (2,1), 19,(2,2). The order of entries is significant since the order of the entries is the same as the order of data record

6. A clustered index on age using Alternative (3).

   1. 11, (1,1), 12, (1, 2), 18,(1,3), 19, (2,1), 19,(2,2). Data records are ordered by age.

7. An unclustered index on gpa using Alternative (1

   1. Cannot build an unclustered index using alternative (1) since the method is inherently clustered.

8. An unclustered index on gpa using Alternative (2).

   1. 1.8, (1,1), 2.0, (1,2), 3.4, (1,3), 3.2,(2,1), 3.8, (2,2)

9. An unclustered index on gpa using Alternative (3).

   1. 1.8, (1,1), 2.0, (1,2), 3.4, (1,3), 3.2,(2,1), 3.8, (2,2)

10. A clustered index on gpa using Alternative (1).

    1. It is not possible to build a clustered index using Alternative (1) because the data file is sorted by age, not gpa.

11. A clustered index on gpa using Alternative (2).

    1. It is not possible to build a clustered index using Alternative (1) because the data file is sorted by age, not gpa.

12. A clustered index on gpa using Alternative (3).

    1. It is not possible to build a clustered index using Alternative (1) because the data file is sorted by age, not gpa.

Explain the difference between Hash indexes and B+ tree indexes. In particular, discuss how equality and range searches work, using an example.

Hash indexes:

• A hash index is a collection of buckets, organized in the form of an array. A hash function maps an element or search key to one of the bucket locations in the hash index. The hash function is selected in such a way that no two search key values point to the same bucket location.

• Insertions and deletions in a hash based index are simple.

• Hash indexes are especially good at equality searches because they allow a record look up very quickly with an average cost of 1.2 I/Os.

  • Assume we have the employee relation with primary key eid and 10,000 records total. Looking up all the records individually would cost 12,000 I/Os for Hash indexes.

• Hash is not good for range queries since the data is not sorted.

B+ trees Indexes:

• B+tree is a tree-type data structure that sorts data and arranges them in a hierarchical fashion for retrieval.

• Inserting and deleting is costly as every time a new element is inserted the entire tree is sorted and is arranged.

• B+ tree have a cost of 3-4 I/Os per individual record lookup.

• B+ tree indexes are more suitable for range queries.

Why issues are considered in using clustered indexes? what is an index only evaluation method? what is its primary advantage?

Clustered indexes

• A file organization for data records

• At most one clustered index on a given collection of data

• There can be several unclustered indexes on a data file.

• A clustered index is expensive to maintain, therefore, used only when there are frequent queries that benefit from it.

• A clustered index is typically built using tree not hashing.

Index-only evaluation method

• The index-only evaluation method refers to the ability to answer a query using only the data stored in an index, without accessing the actual data records in the base table.

  • Index-only plans can also be found for queries involving more than one table.

• Primary advantage is the significant reduction in I/O operations, leading to faster query performance and reduced contention.

What is a composite search key? what are the pros and cons of composite search key?

A composite search key is search key for an index can contain several fields. As an example, consider a collection of employee records, with fields name, age and sal stored in sorted order by name.

• Equality query: every field value is equal to a constant value

  • e.g. <sal,age> index: age = 20 and sal = 75

• Range query: some field value is not a constant

  • e.g. age = 20 or age 20 and sal > 10

Data entries in index are sorted by search key to support range queries.

Composite indexes are larger, updated more often

what sql commands support index creation?

MS SQL Server

CREATE[ UNIQUE ] [ CLUSTERED | NONCLUSTERED ] INDEX index_name ON { table |view } ( column [ ASC | DESC ] [ ,...n ] )

CREATE CLUSTERED INDEX index_name ON table_name (column1, column2, ...);

If you were about to create an index on a relation, what considerations would guide your choice? Discuss:

1. . The choice of primary index.

The choice of the primary key is made based on the semantics of the data. If we need to retrieve records based on the value of the primary key, as is likely, we should build an index using this as the search key. If we need to retrieve records based on the values of fields that do not constitute the primary key, we build (by definition) a secondary index using (the combination of) these fields as the search key.

If you were about to create an index on a relation, what considerations would guide your choice? Discuss:

2. Clustered versus unclustered indexes.

A clustered index offers much better range query performance, but essentially the same equality search performance (modulo duplicates) as an unclustered index. Further, a clustered index is typically more expensive to maintain than an unclustered index. Therefore, we should make an index be clustered only if range queries are important on its search key. At most one of the indexes on a relation can be clustered, and if range queries are anticipated on more than one combination of f ields, we have to choose the combination that is most important and make that be the search key of the clustered index.

If you were about to create an index on a relation, what considerations would guide your choice? Discuss:

3. Hash versus tree indexes

Hash indexes:

• Cannot perform range queries.

• Only going to perform equality queries, for example the case of social security numbers, than hash indexes are best choice since its faster retrieval than B+ trees by 2-3 I/Os per request

B+ trees:

• Can ranged queries are going to be performed.

If you were about to create an index on a relation, what considerations would guide your choice? Discuss:

4. The use of sorted file rather than a tree-based index

First of all, both sorted files and tree-based indexes offer fast searches. Insertions and deletions, though, are much faster for tree-based indexes than sorted files. On the other hand scans and range searches with many matches are much faster for sorted files than tree-based indexes. Therefore, if we have read-only data that is not going to be modified often, it is better to go with a sorted file, whereas if we have data that we intend to modify often, then we should go with a tree-based index.

Choice of search key for the index. What is a composite search key, and what considerations are made in choosing composite search keys? What are index-only plans, and what is the influence of potential index-only evaluation plans on the choice of search key for an index?

A composite search key is a key that contains several fields. A composite search key can support a broader range as well as increase the possibility for an index-only plan, but are more costly to maintain and store. An index-only plan is query evaluation plan where we only need to access the indexes for the data records, and not the data records themselves, in order to answer the query. Obviously, index-only plans are much faster than regular plans since it does not require reading of the data records. If it is likely that we are going to performing certain operations repeatly that only require accessing one field, for example the average value of a field, it would be an advantage to create a search key on this field since we could then accomplish it with an index-only plan.

What main conclusions can you draw from the discussion of the five basic file organizations discussed in Section 8.4? Which of the five organizations would you choose for a file where the most frequent operations are as follows?

1. Search for records based on a range of field values.

2. Perform inserts and scans, where the order of records does not matter.

3. Search for a record based on a particular field value.

The main conclusion about the five file organizations is that all five have their own advantages and disadvantages. No one file organization is uniformly superior in all situations. The choice of appropriate structures for a given data set can have a significant impact upon performance. An unordered file is best if only full file scans are desired. A hash indexed file is best if the most common operation is an equality selection. A sorted file is best if range selections are desired and the data is static; a clustered B+ tree is best if range selections are important and the data is dynamic. An unclustered B+ tree index is useful for selections over small ranges, especially if we need to cluster on another search key to support some common query.

1. Using these fields as the search key, we would choose a sorted file organization or a clustered B+ tree depending on whether the data is static or not.

2. Heap file would be the best fit in this situation.

3. Using this particular field as the search key, choosing a hash indexed file would be the best.

Consider the following relation:

Emp(eid: integer, sal: integer, age: real, did: integer)

There is a clustered index on eid and an unclustered index on age.

1. How would you use the indexes to enforce the constraint that eid is a key?

2. Give an example of an update that is definitely speeded up because of the available indexes. (English description is sufficient.)

3. Give anexample ofan update that is definitely slowed down because of the indexes. (English description is sufficient.)

4. Can you give an example of an update that is neither speeded up nor slowed down by the indexes?

1. Given there enforce the constraint that clustered index eid is a key:

   1. The database system automatically enforces uniqueness for eid.

2. Give an example of an update that is definitely speeded up because of the available indexes:

   1. Index on eid column is a clustered index that speeds up insert, updates, and search operations.

   2. In a clustered index data is sorted and retrieving range-based data from sorted data requires less number of I/O operations and is executed faster.

3. Give an example of an update that is definitely slowed down because of the indexes

   1. Index on age column is an unclustered index. An update operation on an unclustered index column requires more amount of time as data in an unclustered index is not sorted and each record is saved on a different page on the disk.

   2. Updating the age of all employees by adding 5, this operation slows down the process.

4. Can you give an example of an update that is neither speeded up nor slowed down by the indexes?

   1. There is no index on the column “did”, any change on non indexed columns neither slows down nor improves the performance of execution

   2. Updating”did” value of all the records whose did value = “100” to “200”

Consider the following relations:

Emp(eid: integer, ename: varchar, sal: integer, age: integer, did: integer) Dept(did: integer, budget: integer, floor: integer, mgr eid: integer)

Salaries range from $10,000 to $100,000, ages vary from 20 to 80, each department has about five employees on average, there are 10 floors, and budgets vary from $10,000 to $1 million. You can assume uniform distributions of values.

For each of the following queries, which of the listed index choices would you choose to speed up the query? If your database system does not consider index-only plans (i.e., data records are always retrieved even if enough information is available in the index entry), how would your answer change? Explain briefly.

1. Query: Print ename, age, and sal for all employees.

   1. (a) Clustered hash index on ename,age,sal fields of Emp.

   2. (b) Unclustered hash index on ename,age,sal fields of Emp.

   3. (c) Clustered B+ tree index on ename,age,sal fields of Emp.

   4. (d) Unclustered hash index on eid,did fields of Emp.

   5. (e) No index

2. Query: Find the dids of departments that are on the 10th floor and have a budget of less than $15,000.

   1. (a) Clustered hash index on the floor field of Dept.

   2. (b) Unclustered hash index on the floor field of Dept.

   3. (c) Clustered B+ tree index on floor,budget fields of Dept.

   4. (d) Clustered B+ tree index on the budget field of Dept.

   5. (e) No index.

Step 1

a) To retrieve all employee records a simple scan operation is sufficient.

• Clustered hash index is suitable to retrieve records for range based searches. But clustered hash index is expensive to maintain and to retrieve all employees’ records where order of the records is not considered a clustered hash index is of no use. Hence option A is not the correct answer.

• Clustered B+ tree index is suitable for update, insert and range based search operations. Clustered B+ trees indexes are also expensive to maintain and to retrieve all employees record clustered B+ tree index is not suitable. Hence option C is not the correct answer.

• Unclustered hash index is suitable for scan operations. Unclustered hash index is less expensive than clustered index, for retrieving all employee records an unclustered hash index is sufficient to process the query.

• As ename, age and sal, are the fields used in the query an unclustered hash index on ‘eid’ and ‘did’ columns will have no effect. So option D is not correct the correct answer

• An unclustered hash index on ‘ename’, ‘age’ and ‘sal’ is suitable for processing the query. Hence option B is the correct answer.

• When the system has no index only plan, creating an index on the file is of no use. When no index only plans are used option E is the correct answer.

Step: 2

b) To retrieve department information where floor =10 and budget is less than 15000

An index on floor and budget fields must be built.

• To process such query first the floor =10 records are identified and then the budget column satisfying the condition are identified. A sorted file is more suitable for such queries.

• A clustered index on floor field is suitable to process the query as the records are sorted based on the floor field but as budget column is not considered in the index. Option A is not the correct answer.

• In an unclustered index records are not sorted so building an unclustered index slows down the query process. Hence option B is not the correct answer.

• A Clustered B+ tree index only on budget field is not suitable as in the query process first the floor with value 10 is identified, so floor field must also be included in the index. Hence option D is not suitable.

• As only records which are satisfying the condition are retrieved creating index on the file speeds up the process, hence option E is not suitable.

• A Clustered B+ tree index on floor and budget field is suitable for the query as records are ordered based on the floor and budget fields resulting in efficient processing of the query. Thus option C is the correct answer.

Given an unclustered alternative-2 tree index with a tree height of 10, what is the IO cost for finding the matching data entry? What is the total cost for using this index to find a matching data record? Explain why a hash index would perform better.

1. IO cost for finding the matching data entry

   1. Determined by the number of levels that need to be traversed, which is 10. Each level represents a disk IO operation.

2. Total cost for using the index to find a matching data record

   1. Total IO cost = cost to traverse the tree + cost to retrieve the data record (additional IO operation since the index is unclustered)

   2. Total IO cost = 10 + 1 = 11

3. Why a Hash Index would perform better

   1. A hash index could be more efficient as it typically only requires just a single IO operation for any access. This is because a hash function directly maps each data and its location, allowing efficient access directly to the data.

4. Comparison

   1. Tree Index IO cost: 11 IO operations(10 to traverse the tree and 1 to fetch the data record).

   2. Hash Index IO cost: 2 IO (1 to access the hash bucket and 1 to fetch the data record, assuming no collisions).

(2)  If the above index is for the attribute salary, what is the IO cost for finding the 10 employees with a salary higher than $1M?

Using an unclustered alternative 2-tree index is well-suited for range queries because it maintains a sorted order of the indexed attribute, allowing efficient traversal of records within a specified range.

IO Cost = cost to find the starting point + cost to retrieve data records

IO cost = 10 + 10 = 20.

If a clustered index is used, what would be the IO cost for the search operation described in Question 2, assuming each disk page can hold 50 data records?

Using a clustered index for range queries significantly reduces the IO cost because the relevant data records are stored sequentially on disk, minimizing the number of disk page accesses required. In this case, the total IO cost for finding 10 employees with a salary higher than $1M is 11, one page.

Given a heap file containing 10,000 records and an unclustered hash index on the attribute SSN, what is the IO cost for performing an equality search to find a record with a specific SSN?

Equality Search with Unclustered Hash Index:

• Step 1: Use the hash function to locate the appropriate bucket (1 IO).

• Step 2: Scan the bucket to find the specific record (1 IO since each bucket fits into one disk page).

• Total IO cost: 1+1=21 + 1 = 21+1=2 IOs.

Question: Heap File Operations

Problem: Consider a heap file containing 10,000 records, where each record is 100 bytes. Assume each disk page can hold 4,000 bytes.

1. Calculate the number of disk pages required to store the heap file.

2. If the average number of records per page is 40, calculate the IO cost for performing a full table scan.

3. Calculate the IO cost for finding a specific record using an equality search without any indexes, assuming the worst-case scenario where the record is found on the last page.

1. Calculate the number of disk pages required to store the heap file.

Records per page = 4000 bytes (each disk page )/ 100 bytes (each record) = 40

Disk page = 10000 (total number of record) /40 (record per page) = 250

2. If the average number of records per page is 40, calculate the IO cost for performing a full table scan.

IO cost for full table scan = 250 pages.

2. Calculate the IO cost for finding a specific record using an equality search without any indexes, assuming the worst-case scenario where the record is found on the last page.

• Without any indexes, each page needs to be read sequentially until the record is found.

• In the worst-case scenario, the record is found on the last page.

• Number of disk pages to be read:

  IO cost=250 pages\text{IO cost} = 250 \text{ pages}IO cost=250 pages

  So, the IO cost is 250 disk I/Os in the worst case.

Additional Problem: Heap File with Insertion and Deletion

Problem: Given the same heap file with 10,000 records and 250 disk pages:

1. Calculate the IO cost for inserting a new record at the end of the file.

2. Calculate the IO cost for deleting a record, assuming you have to search for the record first and then delete it.

1. Calculate the IO cost for inserting a new record at the end of the file.

• Insertions in a heap file are typically done at the end of the file.

• The IO cost involves writing the new record to the last page.

• Number of disk pages to write:

  IO cost=1 (write to the last page)

1. Calculate the IO cost for deleting a record, assuming you have to search for the record first and then delete it.

searching for the record (as calculated earlier, 250 IOS in the worst case)

Deleting the record from the page, which involves reading and writing the page.

Total IO cost = 250 + 2 = 252 disk I/Os

Question 1: Sorted File for Equality Search

Problem: Given a sorted file sorted on the attribute age, containing 10,000 records, and each disk page can hold 50 records. What is the IO cost for finding a specific record with age = 30? Explain why a B+ tree index might be preferred over a sorted file for equality searches.

Since the file is sorted, a binary search can be used to find the specific record. The binary search on 200 pages (10,000 records / 50 records per page) requires log⁡2200≈8\log_2 200 \approx 8log2​200≈8 IOs. To fetch the specific record requires 1 more IO. Therefore, the total search cost is 8 + 1 = 9 IOs. A B+ tree index might be preferred because it can provide faster search times with fewer IOs, especially if the tree height is less than the depth needed for a binary search in a sorted file.

Question 2: Sorted File for Range Query

Problem: If the above file is sorted on salary, what is the IO cost for finding 10 employees with a salary higher than $100,000?

Answer: A binary search is used to find the starting point for salaries higher than $100,000, which costs log⁡2(200)≈8 IOs. Retrieving the data records of the 10 employees requires additional IOs. Assuming each page holds 50 records, the 10 records might span across 1 page. Therefore, the total search cost is 8 + 1 = 9 IOs.

Question 3: Sorted File for Range Query with More Records

Problem: If the sorted file is used to find 100 employees with a salary higher than $100,000, what is the IO cost assuming each disk page can hold 50 records?

Answer: A binary search is used to find the starting point, which costs log⁡2(200)≈8 IOs. Retrieving the data records of the 100 employees requires additional IOs. Assuming each page holds 50 records, the 100 records might span across 2 pages. Therefore, the total search cost is 8 + 2 = 10 IOs.

Question 4: Insertions in a Sorted File

Problem: Given a sorted file with 10,000 records sorted on the attribute employee_id, calculate the IO cost for inserting a new record.

Answer: Inserting a new record requires finding the correct position using a binary search, which costs log⁡2(200)≈8 IOs. After locating the correct position, inserting the new record may require shifting subsequent records to maintain the sorted order. In the worst case, this could involve moving half of the records, leading to high IO costs. Therefore, the total IO cost is 8 + additional IOs for shifting records, which can be significant depending on the position and number of records to shift.

Question 5: Deletion in a Sorted File

Problem: Calculate the IO cost for deleting a record from a sorted file containing 10,000 records sorted on the attribute SSN.

Answer: Deleting a record requires finding the specific record using a binary search, which costs log⁡2200≈8 IOs. After locating the record, deletion may require shifting subsequent records to maintain the sorted order, which involves additional IOs. Therefore, the total IO cost is 8 + additional IOs for shifting records, which can be significant depending on the number of records to shift.

Question 6: Sorted File vs. Clustered Index for Range Query

Problem: Compare the IO costs for finding 20 employees with a salary higher than $90,000 in a sorted file versus a clustered B+ tree index on salary, assuming the B+ tree has a height of 3 and each disk page holds 50 records.

Answer: Sorted File:

• Binary search to find the starting point: log⁡2(200)≈8 IOs.

• Retrieving 20 records, assuming each page holds 50 records, might span 1 page.

• Total IO cost: 8 + 1 = 9 IOs.

Clustered B+ Tree Index:

• IO cost to find the starting point in the B+ tree: tree height = 3 IOs.

• Retrieving 20 records might span 1 page.

• Total IO cost: 3 + 1 = 4 IOs.

Comparison: The clustered B+ tree index is more efficient with a total IO cost of 4 compared to the sorted file's 9 IOs.

Question 1: Clustered B+ Tree Index

Problem: Given a clustered B+ tree index on a file with a tree height of 3 and 1000 leaf pages, what is the IO cost for finding a matching data entry? What is the total cost for using this index to find a matching data record?

Answer: Since the tree height is 3, the cost of finding the matching data entry is 3 IOs. Because the index is clustered, the data entries are stored along with the data records, so no additional IO is needed to fetch the data record. Therefore, the total search cost is 3 IOs.

Question 2: Clustered Index for Range Queries

Problem: If the above index is for the attribute salary, what is the IO cost for finding 10 employees with a salary higher than $1M, assuming each disk page can hold 50 data records?

Answer: The cost of finding the starting point in the B+ tree is the height of the tree, which is 3 IOs. Since each disk page can hold 50 records, the 10 employees with a salary higher than $1M can reside in 1 disk page. Therefore, the total search cost is 3 + 1 = 4 IOs.

Question 3: Clustered Index for Equality Search

Problem: Given a clustered B+ tree index on the attribute age with a tree height of 2 and 200 leaf pages, what is the IO cost for finding all employees aged 30, assuming there are 20 such employees and each disk page can hold 50 records?

Answer: The cost of finding the starting point in the B+ tree is the height of the tree, which is 2 IOs. Since there are 20 employees aged 30 and each disk page can hold 50 records, they can reside in 1 disk page. Therefore, the total search cost is 2 + 1 = 3 IOs.

Question 4: Inserting into a Clustered B+ Tree Index

Problem: Given a clustered B+ tree index on the attribute employee_id with a tree height of 4 and 500 leaf pages, calculate the IO cost for inserting a new record.

Answer: The cost of finding the correct leaf page to insert the record involves descending the tree, which is 4 IOs. Inserting the record into the leaf page requires 1 IO. If a page split occurs, additional IOs are needed to update the tree. Assuming a split and update to the parent node, the total cost is:

• 4 IOs (descending the tree) + 1 IO (insert record) + 1 IO (split page) + 1 IO (update parent node) = 7 IOs.

Question 5: Deleting from a Clustered B+ Tree Index

Problem: Given a clustered B+ tree index on the attribute department with a tree height of 3 and 300 leaf pages, calculate the IO cost for deleting a record from the HR department.

Answer: The cost of finding the correct leaf page to delete the record involves descending the tree, which is 3 IOs. Deleting the record from the leaf page requires 1 IO. If a page merge occurs, additional IOs are needed to update the tree. Assuming a merge and update to the parent node, the total cost is:

• 3 IOs (descending the tree) + 1 IO (delete record) + 1 IO (merge page) + 1 IO (update parent node) = 6 IOs.

Question 6: Comparing Clustered and Unclustered Indexes

Problem: Compare the IO costs for finding 50 employees with a department_id of 5 in a clustered B+ tree index versus an unclustered B+ tree index, assuming a tree height of 3 and each disk page can hold 50 records.

Question 6: Comparing Clustered and Unclustered Indexes

Problem: Compare the IO costs for finding 50 employees with a department_id of 5 in a clustered B+ tree index versus an unclustered B+ tree index, assuming a tree height of 3 and each disk page can hold 50 records.

Answer:

Clustered B+ Tree Index:

• IO cost to find the starting point in the B+ tree: 3 IOs.

• Retrieving the 50 records can span 1 page.

• Total IO cost: 3 + 1 = 4 IOs.

Unclustered B+ Tree Index:

• IO cost to find the starting point in the B+ tree: 3 IOs.

• Retrieving the 50 records might require 50 IOs (assuming each record needs a separate IO).

• Total IO cost: 3 + 50 = 53 IOs.

Comparison: The clustered B+ tree index is significantly more efficient with a total IO cost of 4 compared to the unclustered B+ tree index's 53 IOs.

Question 1: Unclustered Tree Index

Problem: Given an unclustered alternative-2 tree index with a tree height of 8 and 2000 leaf pages, what is the IO cost for finding the matching data entry? What is the total cost for using this index to find a matching data record? Explain why a hash index would perform better.

Answer: Since the tree height is 8, the cost of finding the matching data entry is 8 IOs. To fetch the matching data record requires one more IO. Therefore, the total search cost is 8 + 1 = 9 IOs. A hash index would perform better because it directly maps the search key to the bucket, typically requiring only 2 IOs: one to locate the bucket and one to read the page.

Question 2: Unclustered Tree Index for Range Queries

Problem: If the above index is for the attribute salary, what is the IO cost for finding 15 employees with a salary higher than $90,000?

Answer: The cost of finding the starting point in the B+ tree is the height of the tree, which is 8 IOs. Assuming each page holds 50 records, retrieving the data records of the 15 employees might span across 1 page (best case) or up to 15 pages (worst case). Therefore, the total search cost ranges from:

• Best case: 8 + 1 = 9 IOs.

• Worst case: 8 + 15 = 23 IOs.

Question 3: Unclustered Tree Index for Equality Search

Problem: Given an unclustered tree index with a tree height of 6 and 1000 leaf pages, what is the IO cost for finding all employees with age = 35, assuming there are 30 such employees and each disk page can hold 50 records?

Answer: The cost of finding the starting point in the B+ tree is the height of the tree, which is 6 IOs. Retrieving the 30 records might span across 1 page (best case) or up to 30 pages (worst case). Therefore, the total search cost ranges from:

• Best case: 6 + 1 = 7 IOs.

• Worst case: 6 + 30 = 36 IOs.

Question 4: Inserting into an Unclustered Tree Index

Problem: Given an unclustered tree index on the attribute employee_id with a tree height of 5 and 1500 leaf pages, calculate the IO cost for inserting a new record.

Answer: The cost of finding the correct leaf page to insert the record involves descending the tree, which is 5 IOs. Inserting the record into the leaf page requires 1 IO. If a page split occurs, additional IOs are needed to update the tree. Assuming a split and update to the parent node, the total cost is:

• Without split: 5 + 1 = 6 IOs.

• With split: 5 + 1 + 1 + 1 = 8 IOs (split page and update parent node).

Question 5: Deleting from an Unclustered Tree Index

Problem: Given an unclustered tree index on the attribute department with a tree height of 7 and 800 leaf pages, calculate the IO cost for deleting a record from the Sales department.

Answer: The cost of finding the correct leaf page to delete the record involves descending the tree, which is 7 IOs. Deleting the record from the leaf page requires 1 IO. If a page merge occurs, additional IOs are needed to update the tree. Assuming a merge and update to the parent node, the total cost is:

• Without merge: 7 + 1 = 8 IOs.

• With merge: 7 + 1 + 1 + 1 = 10 IOs (merge page and update parent node).

Question 6: Comparing Unclustered and Clustered Indexes

Problem: Compare the IO costs for finding 25 employees with a department_id of 7 in an unclustered tree index versus a clustered tree index, assuming a tree height of 4 and each disk page can hold 50 records.

Answer:

Unclustered Tree Index:

• IO cost to find the starting point in the tree: 4 IOs.

• Retrieving the 25 records might require 25 IOs (assuming each record needs a separate IO).

• Total IO cost: 4 + 25 = 29 IOs.

Clustered Tree Index:

• IO cost to find the starting point in the tree: 4 IOs.

• Retrieving the 25 records might span 1 page (best case) or 1 page (worst case).

• Total IO cost: 4 + 1 = 5 IOs.

Comparison: The clustered tree index is significantly more efficient with a total IO cost of 5 compared to the unclustered tree index's 29 IOs.

Question 1: Unclustered Hash Index

Problem: Given an unclustered hash index with 1000 buckets and 10,000 records, each bucket can fit into one disk page. What is the IO cost for finding a record with a specific SSN? Explain why a hash index is more efficient for equality searches compared to a tree index.

Answer: The cost of locating the appropriate bucket in the hash index is 1 IO. Retrieving the data record from the bucket requires 1 more IO. Therefore, the total search cost is 1 + 1 = 2 IOs. A hash index is more efficient for equality searches because it directly maps the search key to the bucket, minimizing the number of IO operations needed compared to a tree index, which requires traversing the tree structure.

Question 2: Unclustered Hash Index for Range Queries

Problem: If the above hash index is for the attribute salary, what is the IO cost for finding 15 employees with a salary higher than $90,000?

Answer: Hash indexes are inefficient for range queries because they do not preserve any order among the keys. Therefore, each matching record might need an individual IO. Assuming each record is in a different bucket, the total search cost is 1 IO to locate the starting bucket plus 15 IOs to fetch each matching record. Therefore, the total search cost is 1 + 15 = 16 IOs.

Question 3: Unclustered Hash Index for Equality Search

Problem: Given an unclustered hash index with 200 buckets on the attribute age and 10,000 records, calculate the IO cost for finding all employees aged 40, assuming there are 30 such employees and they are evenly distributed across 5 buckets.

Answer: The cost of locating the appropriate bucket is 1 IO per bucket. Since the records are evenly distributed across 5 buckets, we need to read 5 buckets to retrieve all 30 records. Therefore, the total search cost is 5 IOs.

Question 4: Inserting into an Unclustered Hash Index

Problem: Given an unclustered hash index on the attribute employee_id with 500 buckets, calculate the IO cost for inserting a new record.

Answer: The cost of locating the appropriate bucket to insert the record is 1 IO. Inserting the record into the bucket requires 1 IO. Therefore, the total IO cost is 1 + 1 = 2 IOs.

Question 5: Deleting from an Unclustered Hash Index

Problem: Given an unclustered hash index on the attribute department with 300 buckets, calculate the IO cost for deleting a record from the HR department.

Answer: The cost of locating the appropriate bucket to find the record is 1 IO. Deleting the record from the bucket requires 1 IO. Therefore, the total IO cost is 1 + 1 = 2 IOs.

Question 6: Comparing Unclustered and Clustered Hash Indexes

Problem: Compare the IO costs for finding 20 employees with a department_id of 5 in an unclustered hash index versus a clustered hash index, assuming there are 100 buckets and each disk page can hold 50 records.

Answer:

Unclustered Hash Index:

• The cost of locating the appropriate bucket is 1 IO per bucket.

• Retrieving the 20 records might require 20 IOs (assuming each record is in a different bucket).

• Total IO cost: 1 + 20 = 21 IOs.

Clustered Hash Index:

• The cost of locating the appropriate bucket is 1 IO.

• Since records in a clustered index are stored contiguously, retrieving 20 records might span across 1 page.

• Total IO cost: 1 + 1 = 2 IOs.

Comparison: The clustered hash index is significantly more efficient with a total IO cost of 2 compared to the unclustered hash index's 21 IOs.