week 11- Problem Solving, Reasoning and Decision Making

Problem Solving Case Study (Goel & Grafman, 2000)

Patient PF

• his right anterior prefrontal cortex was damaged due to a stroke 

• successful architect before the stroke

• he seemed perfectly normal and intelligent 

• however, he lost his ability in architectural design 

kohler's (1917) studies

Köhler’s 1917 studies showed that chimpanzees could solve problems through insight rather than trial-and-error, challenging behaviorist views and supporting Gestalt psychology.

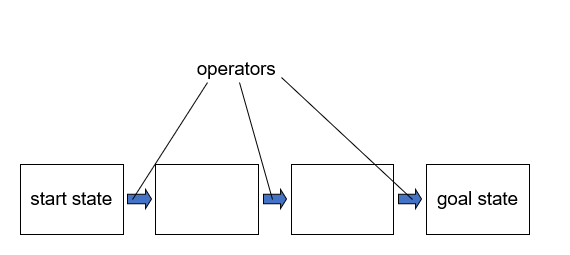
what is a Problem space and a problem state and an operator (dont look at image first)

•Problem space

•Consists of various states of the problem

•Problem state

•A representation of the problem in some degree of solution

•Operator

•An action that will transform the problem state into another problem state

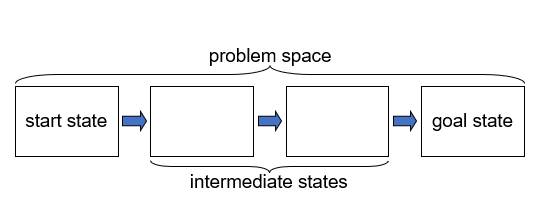
what is problem solving and two important questions 

•Problem solving = searching a sequence of states in a problem space that goes from the start state to the goal state

•Two important questions:

What determines the operators available to the problem solver?

•This defines the problem space

How does the problem solver select a particular operator?

•This determines the path the problem solver will take

3 ways to acquire new operators

•Discovery

•Direct instruction

•Analogy/imitation

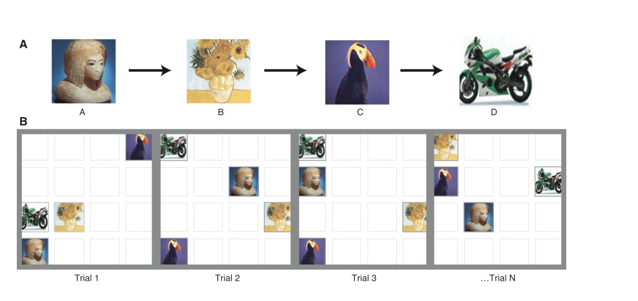
Imitation Subiaul et al. (2004) more monkeys 

•Subiaul et al. (2004) showed that rhesus monkeys can learn how to perform a certain task by looking at other monkeys performing it

• Monkeys who observed the expert learned the sequences faster than those who learned through trial and error.

• This showed they weren’t just copying movements—they were imitating the underlying cognitive rule (e.g., “touch in this order”).

• The effect was robust across multiple trials, confirming that monkeys can engage in rule-based observational learning.

what are the 3 criteria for selecting operators

1.Backup avoidance

2.Difference reduction

3.Means-ends analysis

what is backup avoidance

•The tendency in problem solving to avoid operators that take one back to a state already visited

what is difference reduction

•The tendency in problem solving to select operators that eliminate a difference between the current state and the goal state

•It is a useful method, but not always optimal

•It only considers whether the next step is an improvement and not whether the larger plan will work

what is means-end analysis

Means-ends analysis:

•creates a new subgoal to enable an operator to apply

-An operator is not abandoned even if it cannot be applied immediately

•identifies the biggest difference between the current state and the goal state and try to eliminate it first

How It Works

1. Compare current state to goal state

2. Identify the biggest difference

3. Choose an operation that can reduce that difference

4. Apply the operation

5. Repeat until the goal is reached

This process continues recursively, often creating subgoals that must be solved before the main goal can be achieved.

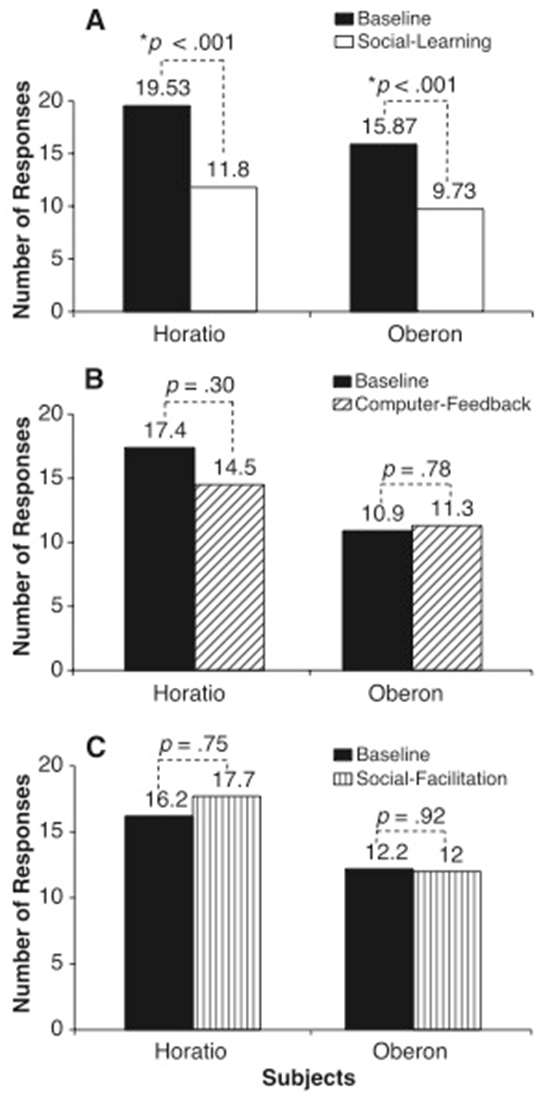
operator selector with tower of hanoi problem

•Difference reduction doesn’t allow you to solve the Tower of Hanoi problem

•People tend to adopt the difference reduction strategy first and then start using means-ends analysis when they try to solve the Tower of Hanoi problem (Kotovsky et al., 1985)

•Patients with prefrontal damage often have difficulty in making backward moves in the Tower of Hanoi problem (Goel & Grafman, 1995)

•They cannot maintain the goal in working memory very well

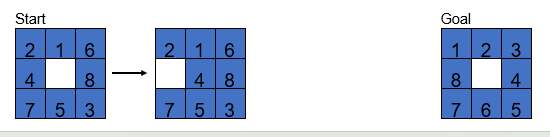
Problem representation

•How states of a problem are represented has significant effects

•

•Successful problem solving depends on representing problems in a way appropriate operators can be applied

•

•e.g., mutilated-checkerboard problem

•Cover the 62 remaining squares using 31 dominos. Each domino covers two adjacent squares

•Or prove logically why such a covering is impossible

• Each domino always covers one black and one white square.

• Removing two same-colored corners (e.g., both white) means there are now 30 white and 32 black squares.

• You can’t pair them evenly → logical contradiction.

🔍 Insight:

• If you represent the board visually with colors, the imbalance becomes obvious.

• If you just think of it as numbers (62 squares, 31 dominoes), it’s harder to spot the issue.

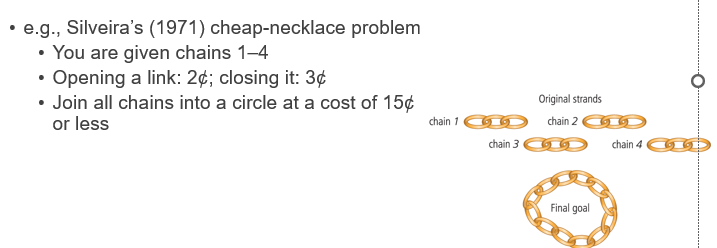
•Incubation effects e.g Silveiras (1971) STUDY cheap necklace problem

•The phenomenon that sometimes solutions to a particular problem come easier after a period of time in which one has ignored trying to solve the problem

Instead, you can:

1. Open all 3 links from one chain → 3 × 2¢ = 6¢

2. Use those 3 open links to connect the other 3 chains together:

   • Each open link is used to close a gap between chains → 3 × 3¢ = 9¢

3. Total cost: 6¢ + 9¢ = 15¢ ✅

•Three groups of participants (they all worked on the problem for 30 min)

•Control: continuous 30 min  55%

•Group 1: interrupted by 30-min of other activities  64%

•Group 2: interrupted by a 4-hour break   85% 

•Incubation effects occur because people forget inappropriate ways of solving problems

Reasoning and decision making AND •Four areas where human irrationality is often found:

•Faced with logical problems, people often come to conclusions that are judged as incorrect from the perspective of formal logic and mathematics

•On the other hand, computer systems that are based on formal logic make so many silly mistakes that humans never make

•Four areas where human irrationality is often found:

•Reasoning about conditionals

•Reasoning about quantifiers

•Reasoning about probabilities

•Decision making

Reasoning about conditionals

•Conditional statement

•If A, then B

•An assertion that if an antecedent (A) is true, then a consequent (B) must be true

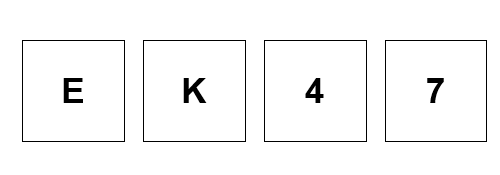
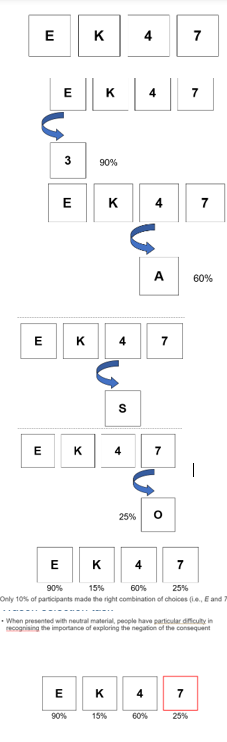
Wason selection task

If a card has a vowel on one side, then it has an even number on the other side

•In other words, neither a vowel nor a consonant on the other s

Your job: Which cards must you turn over to test the rule?

✅ Correct Answer

• Turn over E: To check if the other side is an even number (required by the rule).

• Turn over 7: To check if the other side is a vowel (which would violate the rule).

Do NOT turn over 4 or K—they don’t help falsify the rule.

•When presented with neutral material, people have particular difficulty in recognising the importance of exploring the negation of the consequentide of 4 will falsify the rule.

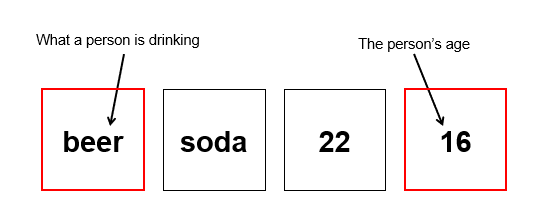
Permission Schema and STUDY •Griggs and Cox (1982)

•Performance on the selection task can be enhanced when the material has meaningful content

•Griggs and Cox (1982)

•“If a person is drinking a beer, then the person must be over 19.”

•74% of participants selected the logically correct combination

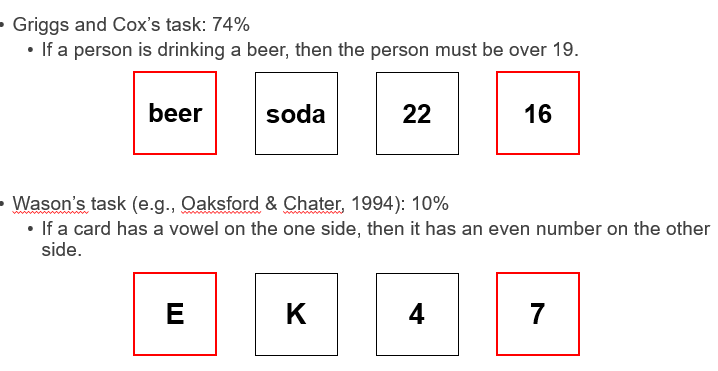
when the material has meaningful content is performance on a selection task enhanced? in terms with Wason and Griggs & Cox

YES, Wason is 10% right with Griggs and Cox's 75% right! big difference 

•Permission schema

•When the conditional statement is interpreted as a rule about what should be the case, performance on the Wason’s selection task tends to be enhanced

It means that when we interpret the conditional statement as a normative rule (what should happen), our brains are more motivated and better equipped to spot violations. We shift from abstract logic to social reasoning, which we’re naturally good at.

Probabilistic interpretation •Why do we perform so poorly on the Wason selection task?

•People tend to select cards that will be informative under a probabilistic model, not a strict logical model

•If A, then B

  → B will probably occur when A occurs

Probabilistic interpretation •Oaksford and Chater (1994)

•“If a car has a broken headlight, it will have a broken taillight.”

•Finding cars that have broken headlights would be reasonable

•There wouldn’t be many of them anyway

•If you find one, it is necessary to check its taillight

•However, do you really want to check all cars  that have intact taillights?

•Cars with broken headlights/taillights are very rare

•Thus, if you find a car with a broken taillight, checking it to see whether it also has a broken headlight helps you make reasonable inference

•It is not logical, but informative choice

•We tend to interpret conditional statements on the basis of a probabilistic model, not a strict logical model

•because doing so actually makes sense in many situations in real life

•This might be one reason why making the correct (= logical) choice in the original Wason’s selection task is so difficult

Reasoning about probabilities, •Prior probability,•Posterior probability

•Prior probability

•The probability that a statement is true before consideration of the evidence

•Posterior probability

•The probability that the statement is true after consideration of the evidence

•To calculate the posterior probability, you need to take into account:

•Prior probability (base rate)

•Evidence

•How reliable the evidence is

•Bayes’s theorem computes the posterior probability

•Don’t worry about its mathematical details!

what is •Base-rate neglect and •Hammerton (1973)

•People often fail to take base rates into account in making probability judgments

•Hammerton (1973)

•Suppose you take a diagnostic test for a rare form of cancer

•Only 1 in 10,000 people has this cancer

•This cancer results in a positive test 95% of the time

•If a person does not have the cancer, the probability of a positive result is 5%

•

If you get a positive result, how do you feel about it (well bad duh)

•Many people feel that the positive result means their chance of actually having the cancer is 95%

•However, the fact that this type of cancer is very rare (0.01%) is not taken into account

•The actual probability of having this cancer (given the positive result) is only 0.19%

•Judgements of probability/frequency and •Tversky and Kahneman (1974)

*decision making

*decision making and subjective utility 

•The subjective value tends to decrease more steeply in negative direction

•Which one would you choose?

•No gain/loss with probability = 1

•0 x 1 = 0

•+1 million dollars with probability = 1/2, or  −1 million dollars with probability = 1/2

(1 million $ x 1/2) + (−1 million $ x 1/2) = 0

•People make decisions under uncertainty in terms of subjective utilities and subjective probabilities