Stats level 3 (Midterm 1)

Statistical analysis doesn’t eliminate uncertainty, but it allows us to

quantify it so we can decide how much we’re willing to live with

Descriptive Statistics

describe the
properties of a
sample

Inferential statistics

uses properties
of the sample to make conclusions
about the population

Examples of descriptive statistics

Sample statistic mean and we calculate M from our sample data

A representative sample is a useful for

inferring population parameters

Random sampling is the best technique to obtain

Representative samples

We are using data from a sample to estimate the truth about a
much larger population

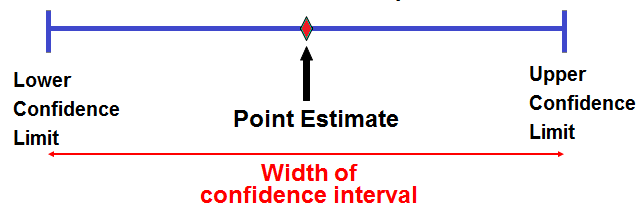
The Estimation Approach

Samples are not a perfect guide to the population; therefore, we
express our uncertainty by reporting a

point estimate and a
confidence interval

The point estimate is our

best single guess about the population, it is
exactly what we found in the sample

The Margin of Error (MoE) is the

likely largest error in the point
estimate

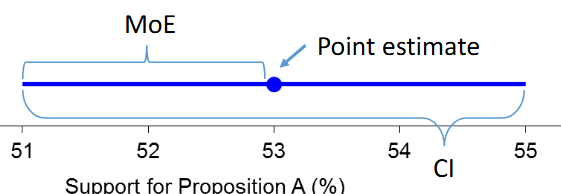
The Confidence Interval (CI) is the

point estimate +/- the MoE

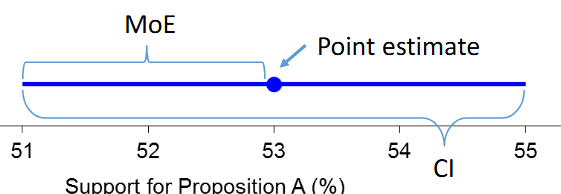
The Confidence Interval (CI) quantifies our

uncertainty about the population. It gives the range of population values which are plausible or likely given the sample data

When we have a Short CI

-> Precise estimate -> Little uncertainty

When we have a Long CI

-> Not a precise estimate -> Lots of uncertainty

What counts as a short and long CI is a

Matter of judgement

How do we get more certainty in our CI

Collect more data! 4x the sample size typically cuts the CI by ½

If you replicated a poll with a new sample, would you reach
exactly the same result?

Probably not! There is sampling variability—differences due to using
different samples to draw conclusions about the population.

• It will probably be close, though! The most likely result of the
replication is an answer within the CI of the original study!

Sampling variability:

Each sample gives somewhat
different results
The Estimation Approach: A simple
example

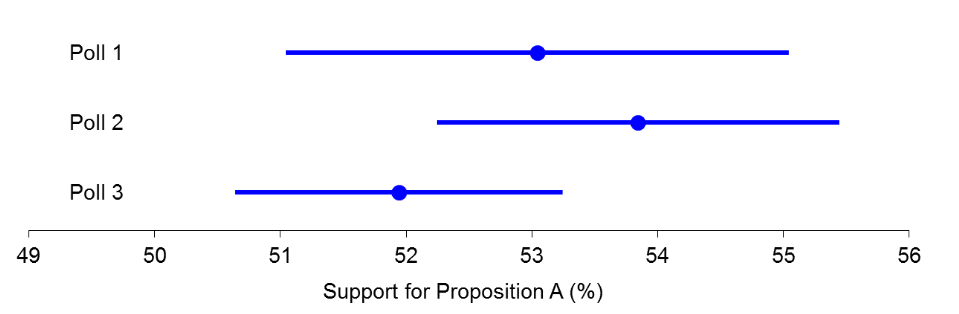
• If we conduct replications, we can conduct a

meta-analysis to synthesize or integrate the results

What does a meta-analysis ensure?

we are examining the whole story, and it gives us an overall estimate more precise than any one study

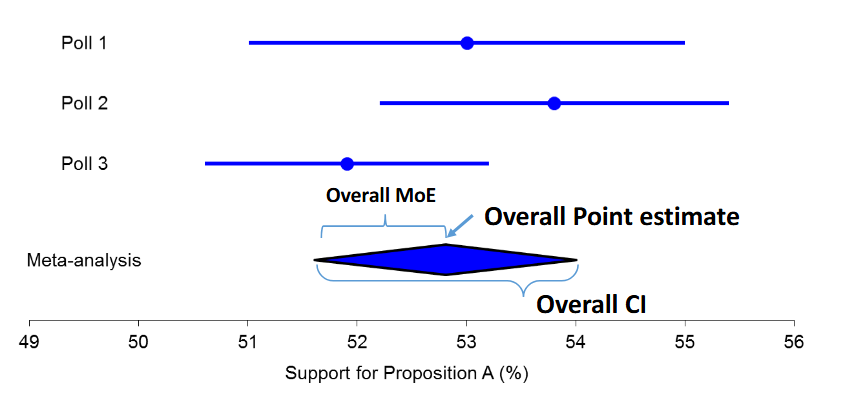
How are the results of a meta analysis summarized?

in a forest plot and the diamond indicates the overall point estimate and CI.

What are the basic principles of a research design

1: Random sampling

2:Experimental vs non-experimental studies

3: Measurement

Random sampling is the 

• Fundamental Assumption in statistical inference

Measurement include

• Operational definitions

• Reliability/Validity

• Levels of Measurement

• Every member of the population has an equal probability of
being chosen.

• All members of the sample are chosen independently.

Random Sampling

• Statistical inference, including the use of Confidence

Intervals, assumes

the data are from a random sample.

In practice, random samples can be difficult to obtain:

• Most psychology research is conducted with young university-

educated adults between 17 and 30 years of age

• Experiments include

• One or more variables are manipulated or assigned by the researcher

• Independent Variable (IV): the variable that is manipulated

• Dependent Variable (DV): the outcome that is observed

• Can justify causal conclusions; confounds controlled (random assignment)

• Describe with causal language: affects/effects, produces, causes, makes

In experiments, the independent variable is the variable that is

being manipulated

In experiments, the dependent variable is the variable that is

the outcome being observed

In experiments, they can justify 

causal conclusions; confounds controlled (random assignment)

• Non-Experiments:

• No manipulation or assignment

• Can not justify causal conclusions; cannot rule out confounds

• Describe with association language: relates to, associated with, correlated with

Non-experiments do not have

manipulation or assignments

Non-experiments cannot

justify causal conclusions; cannot rule out confounds

What is the language used in non-experiments

association language: relates to, associated with, correlated with

What is the language used in experiments

causal language: affects/effects, produces, causes, makes

What is a construct

• The abstract concept we are interested in

What is an operational definition

• A precise procedure for measuring values that represent a construct

What is a measured variable

• The actual variable measured

The measured variable should be

Reliable and Valid

Reliable is

Repeatable;

similar results on repeated

measurement

Valid is

Accurate, true,

measuring what it is meant to

measure

In NOIR, the N is

Nominal

In NOIR, the O is 

Ordinal

In NOIR, the I is

Interval

In NOIR, The R is

Ratio

Nominal is the

Numbers represent characteristics according to a simple

code

a level of measurement in statistics that categorizes data into distinct, non-ordered groupsa level of measurement in statistics that categorizes data into distinct, non-ordered groups

Ordinal is the 

Numbers are assigned based on rank amount of

characteristic:

Interval is the 

• Numbers are assigned based on relative quantity of

characteristic, with no true 0 point

• Examples: year, longitude, latitude, temperature

Ratio is the

• Numbers are assigned based on the absolute

magnitude of a characteristic. The scale has a

true zero point.

What are the two ways a variable can be classified?

Continuous & Discrete

A continuous Variable is a

variable that can take any of

the unlimited number of values in some range.

What are examples of continuous variables 

Height & time spent on a task

A discrete variable is a

variable that can take only distinct or separated values.

What are examples of discrete variables

Number of eggs in a basket, Children in a family,

Toys in a box

Continuous variables can take values

along a smooth curve

discrete variables cannot

take values along a smooth curve

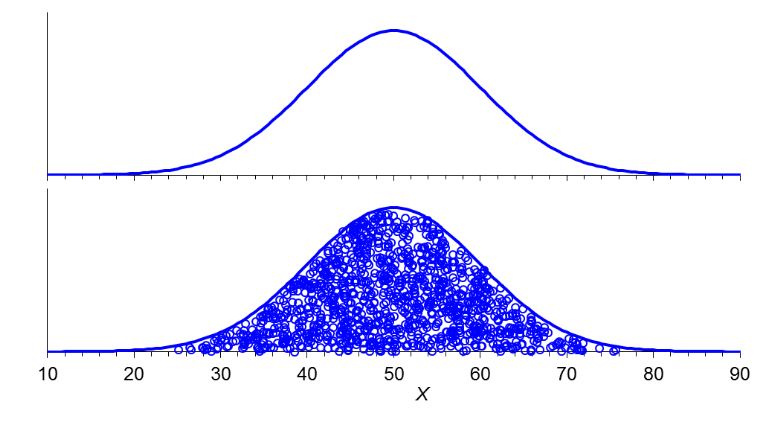
The probability distribution of a continuous variable is a

smooth curve—like this normal distribution you may

remember seeing

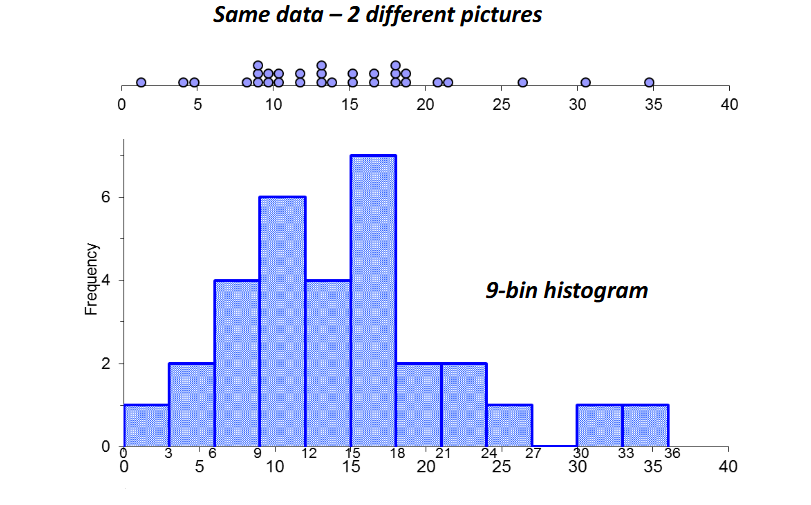
• Histograms depict

the data sorted into bins – each bin contains

X observations of values contained within that bin

What is included in the measure of central tendency?

Mean, Median, and Mode

What is included in a spread?

Standard deviation, Variance, Range, Inter-quartile range

What is the symbol for summation

Σ

What is the mean formula

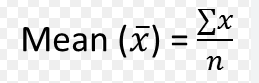
The mean is also known as the

average

M is for the

Sample

μ is for the

population

The mean represents the 

balancing point for the distribution 

Is the mean influenced by outliers?

Yes, especially in small data sets

The median is the

middle point in the distribution, the score at which half the others are above and the other half below (50th
percentile)

Only requires interval scaling; can be used for any type of data

except nominal

Median

The median is not 

as sensitive to outliers as the mean

The mode is

whatever response is most frequent.

Requires only nominal scaling; can be used for any type of

data and is Not very sensitive to outliers

The mode

• Characteristics of the normal distribution:

• Smooth, symmetrical bell shape with most data points near center

• Normal curve defined by two parameters: mean and SD

Normal distributions are not always the same 

• Some are much narrower, some wider

• Mean and SD can vary between distributions

The range is

-The distance from the minimum score to the maximum score

• Easy to understand, but can change dramatically with outliers

or even just with some new data.

The better way then the range is the

SD

What is the formula for the sample SD

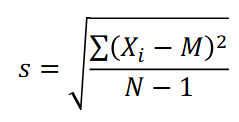
For the SD

—Each data point, there is a possible deviation from the mean (X-M)

• Think of the standard deviation as the average or typical deviation from the mean

s is the symbol for the

Sample SD

σ is the symbol for the

Population SD

The SD is sensitive to

outliers

The Standard Deviation is the square root of

the variance,
another measure of spread

What is the formula for the variance

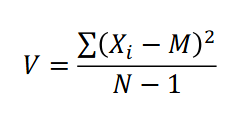
• Variance is useful, but

expressed spread in squared units,

which are a bit difficult to understand.

• Interquartile Range (IQR) only requires

Ordinal scaling and is not very sensitive to outliers 

The z score at the mean is 0, as labeled.

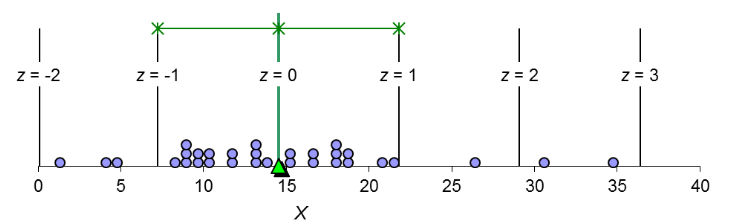
• A z score expresses an individual’s score in

standard

deviation units.

What is the z-score formula

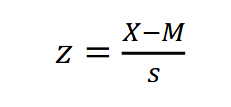
What is the formula for turning a z-score back into a raw score

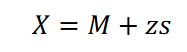
z scores provide standardization

once expressed in z scores, no

need to worry about range of measurement (1 to 10 scale, 1-7 scale,

etc.) or units (inches, feet, etc.)

• z scores allow comparisons across

different measures with different

scales

Percentile% is the

% of data below a score, X

• Only requires ordinal scaling

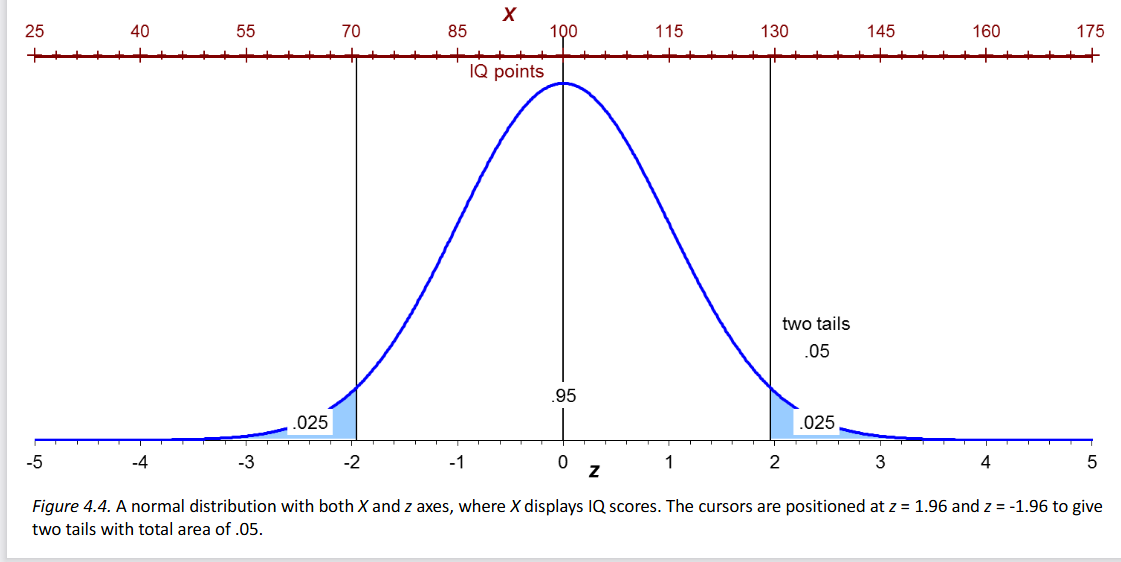
If we transform each observation from a population into a z-
score and then examine how these z-scores are distributed, we
get the standard normal distribution always has a mean

of

0 and standard deviation of 1

Mean uses

Interval or Ratio scaling

Median uses

Ordinal, Interval, or ratio scaling

The mode uses

NOIR scaling

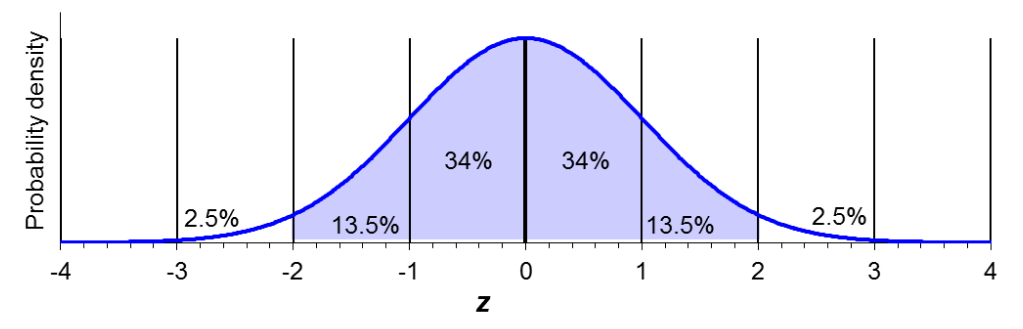
The distribution is labeled with z scores and

corresponding percentages—these represent how much of the

distribution falls between any two z scores

We know M and s for our

Sample

• M and s are expected to change

from

Sample to Sample