Week 2 Data, Statistics, and Visualization

Critical Factors for Data

• Source reliability

• Accuracy

• Accessibility

• Security/privacy

• Richness

• Consistency

• Currency/timeliness

• Granularity

• Validity

• Relevancy

Structured Data

• Easier for computers to process

• Categorial vs. numerical.

• Categorical variables classify information into categories, e.g., nationality, college major, breed (animals).

• A variable is numerical if meaningful arithmetic can be performed on it, e.g., age, income, service duration.

• Ratio data takes values only from zero and above, allowing for reference to multiples.

Unstructured data

Easier for humans to process/digest

Semi-structured data

XML, HTML, Log files, etc.

Elements of Structured Data

• Variable: characteristic of members of a population (e.g. age, gender)

• Observation: conceptually, what is observed for a variable with respect to a member of the dataset.

• Value: the specific datum (number, letters, etc.) observed for one variable with respect to a member of the dataset

Mean

…of a set of numerical values is the arithmetical average of all values in the set. For example, the mean � 𝑿 𝑿 of n observations 𝑋𝑋1,…, 𝑋𝑋𝑛𝑛 is � 𝑿 𝑿 = ∑𝑖𝑖=1 𝑛 𝑛 𝑋𝑋𝑖𝑖 �

Mode

…of a set of numerical values is the value that appears most frequently. There can be more than one mode or no mode at all … it depends on the data.

Median

The middle observation when data are sorted from smallest to largest.

• If number of observations is odd, median is the middle observation.

• If number of observations is even, median is average of the two middle observations.

• The median is more robust to outliers than the mean. • Outliers are values that are ‘unusually large or small’ compared to the range of most other values.

• Large outliers will have a large effect (positive or negative) on the mean, but median will generally not change much

Quartile

Divides the data into four groups, each with a quarter of all observations

• 1st quartile (25th percentile): 25% of observations below it

• 2nd quartile (50th percentile / median): 50% of observations below it

• 3rd quartile (75th percentile): 75% of observations below it

• 4th quartile (100th percentile / maximum): all other observations below it

Variance

A measure that quantifies the amount of variability in numerical data. (denoted by 𝜎𝜎2 – ‘sigma squared’)

• is in squared units: for example, if observations are measured in dollars or minutes, the ________ is in dollars squared or minutes squared.

Standard Deviation

A measure of variability that is easier to interpret is the_________: the square root of variance

• is measured in the same units as the original variable and observations.

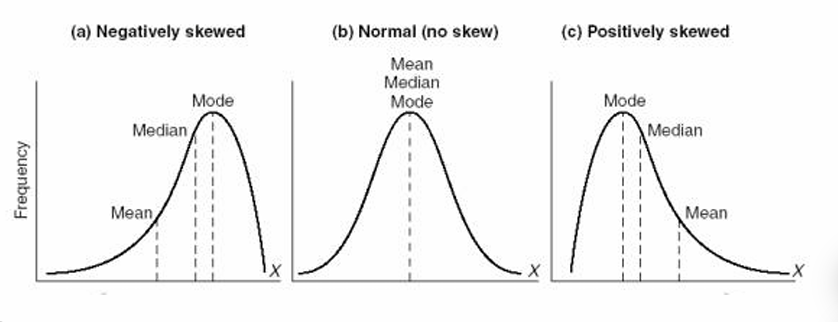
Skewness

A measure of symmetry (or lack of symmetry).

• _______ of the values of a numerical variable is compared to normal distribution (symmetrical, skewness is close to 0).

• The values of a numerical variable can be ____ to the right (or positively ____) because of some very large values.

• The values of a numerical variable can be _____ to the left (or negatively _____) because of some very small values

Data Visualization

The use of visual representations to explore, interpret, and communicate data or information derived from the data.

• Goal: present key insights from data in ways that reduce the cognitive burden for the audience – in a business context, typically someone who needs to make a decision.

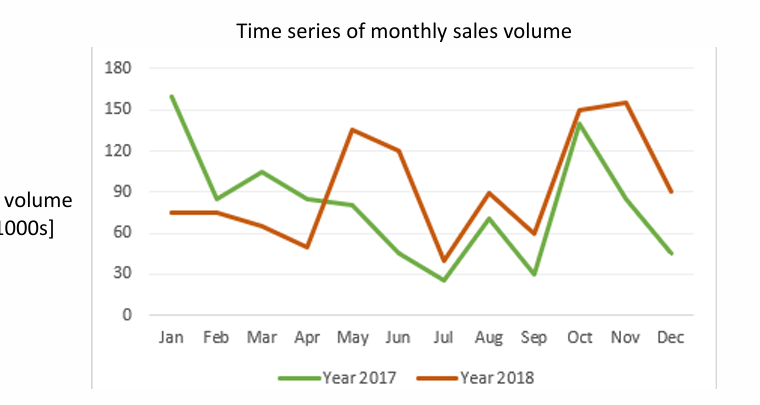
Line Graphs

Good when there is progression of a variable, e.g., with respect to time (called ‘time-series’ data).

• Sequentially connects data points of a variable.

• Often one axis is time: track changes or trends over time.

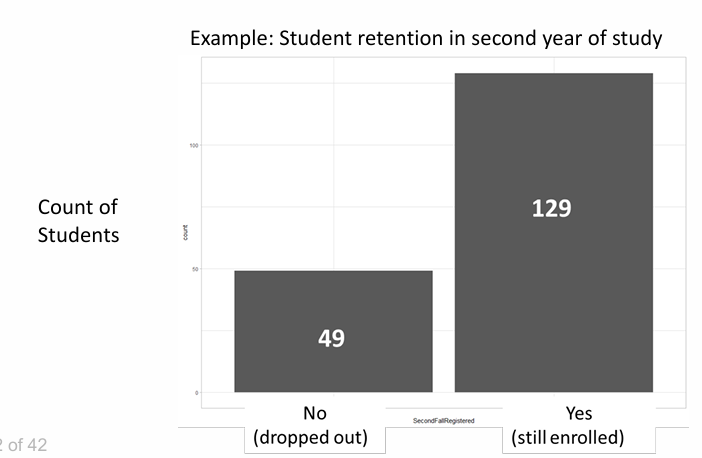
Bar Charts

Useful for depicting nominal or numerical data that is naturally categorized.

• Splits categorical or numeric data into different categories

• Compare data across the categories

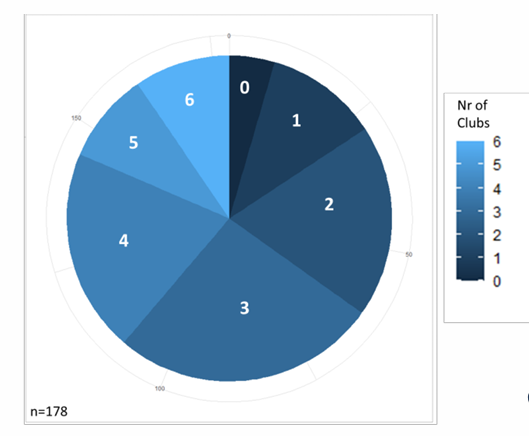
Pie Charts

Used to depict proportions within a variable.

• Shows relative proportions in data for a variable

• Example: Number of high school clubs that applicants to an undergraduate program served as an officer

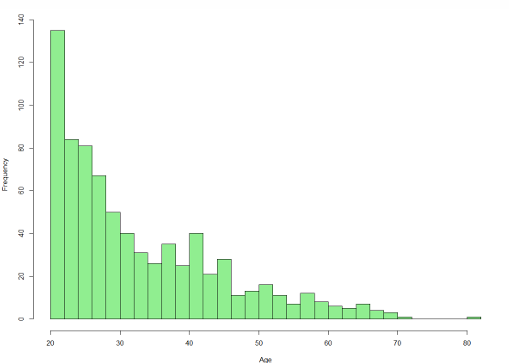
Histograms

Shows frequency distribution for a variable

• Shows the distribution of a numerical variable

• Divide the horizontal axis into bins (usually of equal length)

• Draw a rectangle over each bin with the area of the rectangle proportional to the number of observations in that specific bin.

• Number of bins determines granularity.

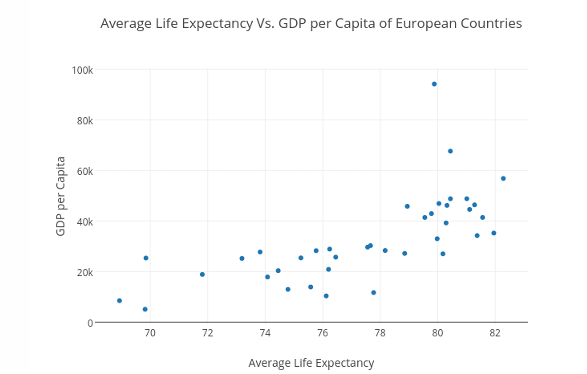
Scatter Plots

Illustrates relationships between two or more numerical variables.

• Shows a scatter of points where each point denotes the values of an observation for two numerical variables

• Detects relationships between two numerical variables, often labeled as X and Y

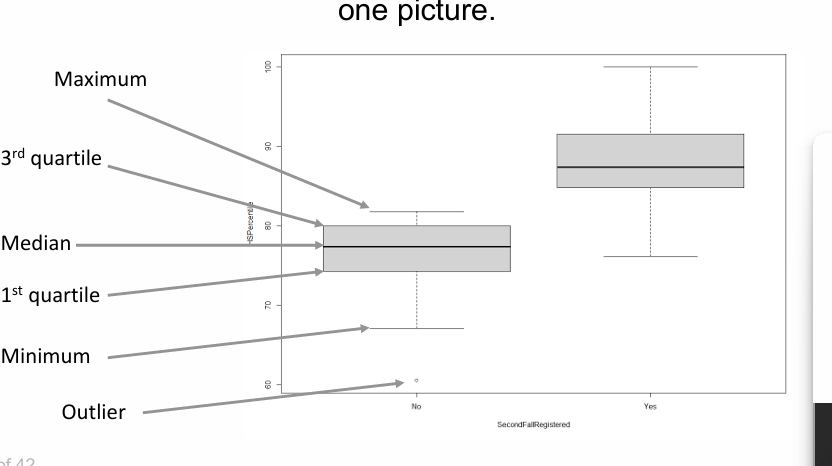
Boxplots

Shows key descriptive statistics for a numerical variable, e.g., minimum, maximum, median, first and third quartiles.