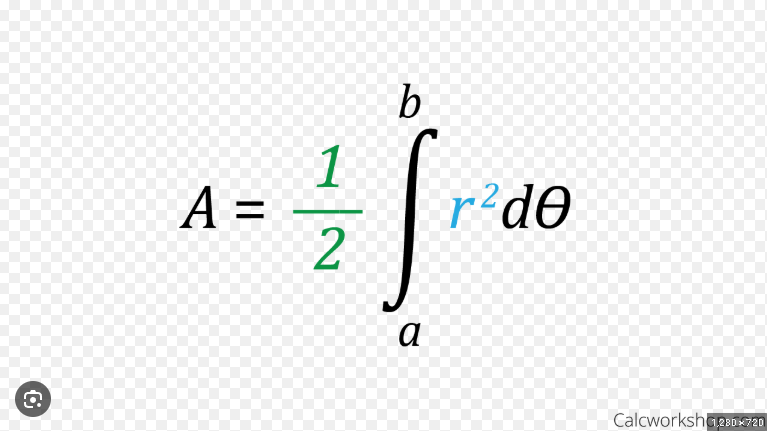Math Equations to Memorize

Area Between Two Curves

A=∫_b^a​[f(x)−g(x)]dx, if using y-axis, use y-coords in integral

Method of Discs & Washers

Or integral from a to b pi times f(x)², if hole between graph and function use washer method, or integral from a to b pi times outer - inner, both squared. For this and all others besides shells, axis matches values on the integral

Method of Cylindrical Shells

For x-axis: Integral from c to d(2pi*y(f(x))

For y-axis: Integral from a to b(2pi*x(g(y)))

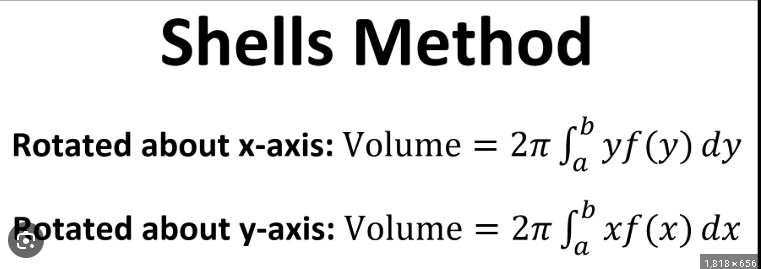
Arc Length

Matches axis of rotation,

x-axis: Integral from a to b(sqrt[1+(f’(x))²])

y-axis: Integral from c to d(sqrt[1+(g’(y))²]

Surface Area

Matches axis of rotation,

x-axis: Integral from a to b(2pi(f(x)) * sqrt[1+(f’(x))²])

y-axis: Integral from c to d(2pi(g(y)) * sqrt[1+(g’(y))²])

Integration by Parts

Remember LIATE, log, inverse trig, algebraic, trig, exponential

Select the u to be LIATE determination

Integral of u dv = u*v - integral(v du)

Each part is an actual value, u and dv are in the first equation, du is derived u, and v is integrated dv. (dv includes the dx term)

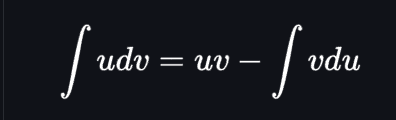
Trig Integral Important Identities

The following identities are important

sin²x + cos²x = 1

sin²x = (1-cos2x)/2

cos²x = (1+cos2x)/2

sec²x - tan²x = 1

csc²x - cot²x = 1

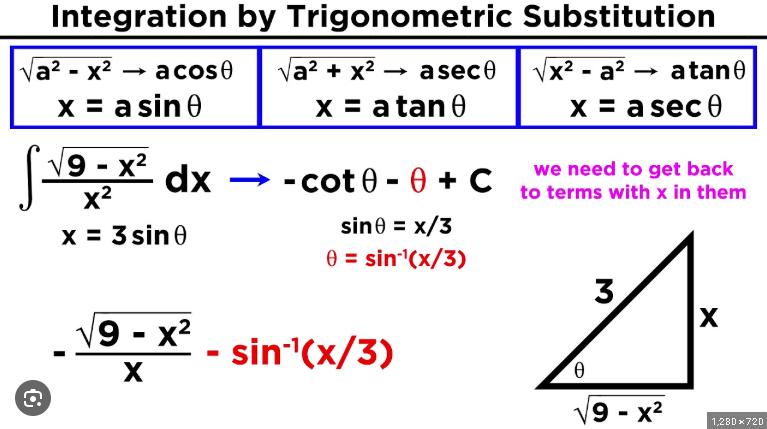
Trig Substitutions

Look under the square root, find which forms match

a²-x²; set x = a*sin(theta)

a²+x²; set x = a*tan(theta) (Cross in + and t)

x²-a²; set x = a*sec(theta) (A is SECond)

Use the original form of x = a*trig(theta), solve for theta and plug into a triangle. Solve for x

Improper Integrals

Take the bad part (inf or DNE part of domain) and set a lim and L.

If DNE is in middle of domain, like x = 1 DNE and domain is [0,3] split into two integrals and use lim thing for both, approaching from the side the function exists.

Separable Diff EQ

Get the dy and dx on isolated side with the terms with that variable, then integrate both sides

First order Linear

Will be in the form y’ + P(x)y = Q(x), if not need to get it into this form

When in the form, set u = e^integral(P(x)), then multiply the whole thing by mew

When this is done, a product rule is made. Set up du/dx (u = the e^ thing) and solve by integrating both sides.

You’ll end up with a C, if IVP use the values to figure out C

Parametric Curve derivative

C’ = dy/dt / dt/dx, basically y’ / x’, x and y are give by C: (x,y)

Arc Length of Parametric Curve (In form C: (x,y))

L = integral from a to b(sqrt[(x prime)²+(y prime)²] dt

Basically Integral from a to be for the square root of the derivatives added and squared

Surface Area for Parametric Curves

Translating Polar and Cartesian

y = r*sin(theta)

x = r*cos(theta)

r = x² + y², theta = tan^-1(x/y)

Shape of Polar Equations

Cardioids: Anything with a -/+, is a cardioid, sin ones go up and down cos ones go left and right. Sign indicates where the long end goes, so if its a - acos the long end points in the -x direction.

Circles: In the form 2acos, or just r = a, with center at x = a if cos and y = a if sin

Rose Curves: In the form a trig (ntheta). If n is even, has 2n petals. If odd, has n petals

Area of Polar Curves

For cardioids and circles range is 0 to 2pi, for rose curves set r =0 and solve to find bounds for one petal, then if problem asks for whole area multiply by amount of petals.