BMM Module 6: Potential Energy surface

Relation PES and FF

PES= full energy landscape of a moleucle, showing how energy changes with atomic positions

Force field= simplified mathemeatical model (using equations and paramaters) to aporximate that landscape

Relation: FF provide an approximate PES that simulations can explore

Relation to MD

Gradient of PES= negative slope of PES at a certain postion = force acting on atoms

MD simulations use FF to calculate these force to navigate the PES

What is the PES?

it maps every possible conformation to it’s energy, allowing us to predict which conformations are the most stable and/or the most populated

• Boltzmann distribution determines the populations

  • the deeper the well depth the more populated

  • transitions occur through saddle point by structural changes

• It gives a 3N dimensional landscape (N= number of atoms)

  • it can’t be visualised

  • you can visualise a 2D slice when varying two coordinates (like torsion angles) while keeping all other others fixed

• at minima:derivative of the energy is 0, so the force acting on it is 0 and it’s in a stable conformation

Goal molecular modelling

Identiy, characterize and navigate between the minima of the PES

How to navigate the PES

Simply minimizing E (goin downhill) is not enough for complex processes like protein folding or ligand docking where many local minima exist so you need sampling techniques to explore multiple minima and find the global one:

• Monte carlo: randomly generates a new conformation, accepts or rejects based on energy and repeats this a lot of times which allows broad exploration of the landscape quickly

• Simulated annealing= type of monte carlo with gradually decreasing temperature, this allows the system to escope local minima in the beginning and later settle into low energy conformations

• Molecular dynamics: solves newtonian equations of motion for all atoms, the system continuously moves over the PES over time, this captures the thermally most accessible position

• Genetic algorithms

PES of propane

• it has 11 atoms so a total of 33 coordinates = 33 variables that define the PES

Total number of paramaters

• 10 covalent bonds

• 18 bond angles

  • each carbon atom is connected to 4 atoms, and these four atoms form bonds with each other

  • atom 4 forms bond with 3 others, atom 3 with 2, atom2 with 1 = 3+2+1 = 6 or (N*(N-1)/2)

  • 6×3 carbon centers

• 18 torsion angles

• 27 non bonded terms

  • 11×10/2 = 55 atom pairs

  • 10 are bonded

  • 18 are connected via bond angles and are not counted

  • 55-10-18 = 27

  • non bonded terms are counted twice for coulomb AND vdw

• =27×2+18+18+10= 100 parameters

XYZ parameters are the independent positional degrees of freedom of the atoms, while bonded and non-bonded parameters are force-field energy terms that depend on and are coupled through those Cartesian coordinates.

Bonded and non-bonded interaction terms are functions of the Cartesian (xyz) coordinates and are fully determined by them.

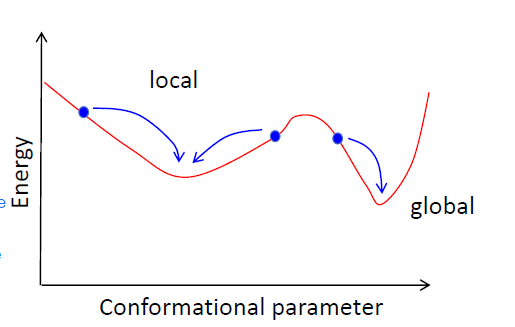
Minima

LMEC= local minimum energy conformation

GMEC= global minimum engergy conformation

• gmec is not always the most populated: a wide valley that is higher in energy might be more populated than a steep lower energy conformation

• prion disease = normal protein misfolds into deep low energy conformation, which is stable, resists degradation and induces other proteins to misfold leading to aggregates that can dammage neurons

EM workflow
EM vs forcefields

(not really in slides but just for clarity)

• 1)build molecule with molecule editior or importing coord,

  • geometry is a rough guess, you rarely start from a stabble conformation

• 2)assign a MM force field that describes how atoms interact and provides the PES

• 3) EM algorithms use the FF to calculate forces on each atom and iteratively move the coordinates to lower the energy

• 4)output = new xyz coordinates of atoms and the minimized structure is then used for tasks like

  • ligand binding

  • docking

  • MD simulations

EM methods

• non-derivative methods

  • simplex method

  • sequential univariate method (bad)

• derivative methods

  • steepest descent

  • conjugated gradient

simplex method

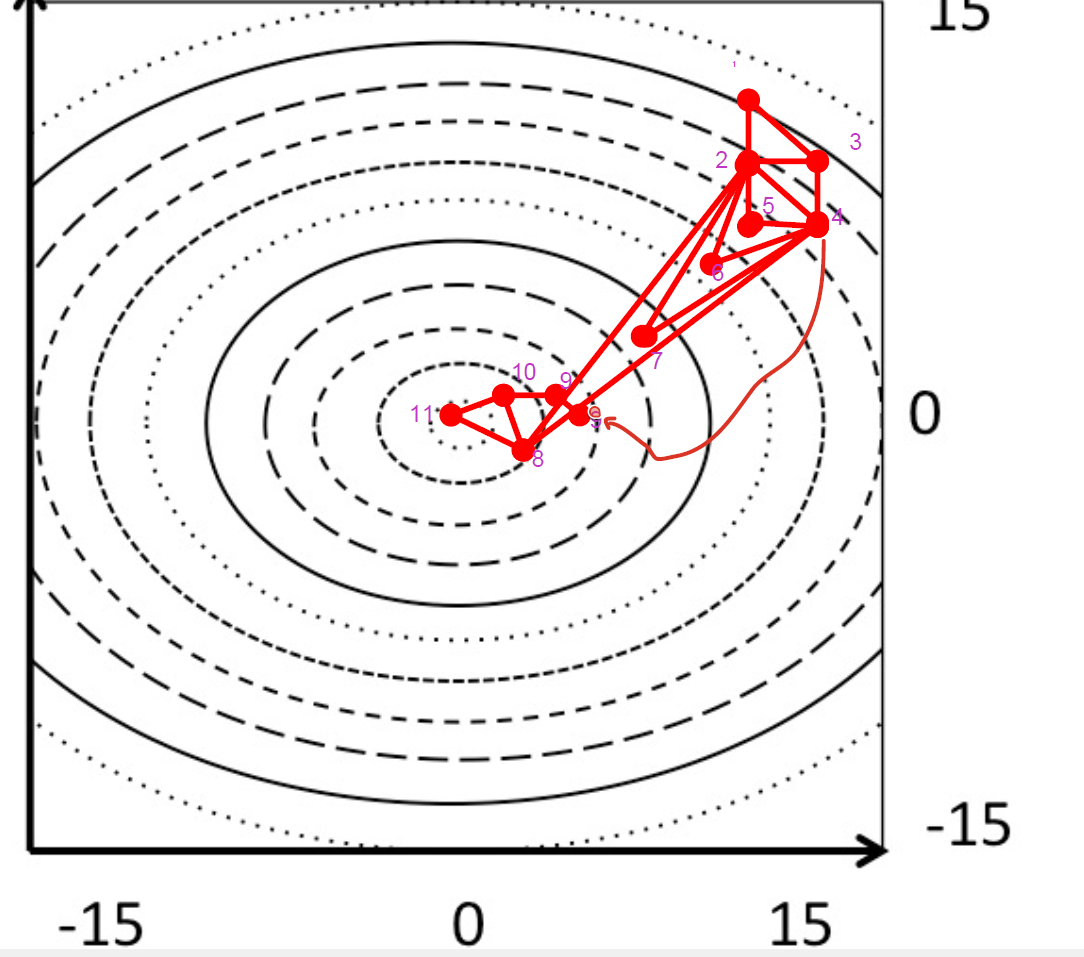
EM algorithm that finds local minima in N-dimensional space for small molecules

simplex= geometric figure with N+1 vertices (corners) each with their own energy

• 1)start with random poin on PES with N neighbouring points

• 2) ID highest E point and reflect through the centroid of the lower energy points

• 3) if reflected point:

  • improves the situation: stretch further along the reflection direction

  • doesn’t improve: move point partially back towards the centroid and then contract the the vertices of higher E towards the lowest E one

• 4) repeat until a local minimum is found

• useful when inital energy is very high and good for intial steps

• but costly in comp time,

  • needs many conformations and E’s before it can start

  • can get trapped in local minima and converges slowly once close to minimum, so better to swithch to other methods at that point

sequential univariate method

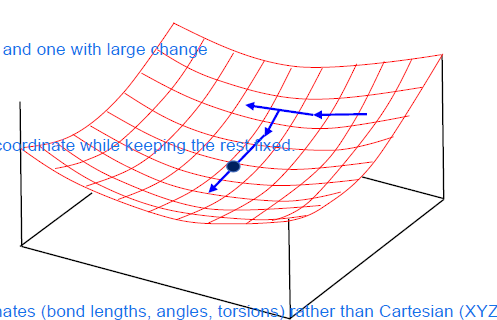
= EM method by optimizing one internal coordinate at a time: xi= bondlengths, bond angles and torsion angles rather than cartesion coordinates

• 1) start wiht conformation xi

• 2) create two new structures xi+deltaxi and xi+2deltaxi and compute the energy

  • one wiht big change and one with small

• 3)fit parabole through the three points and determine the minimum xi+1 = xi+a*delta*xi

• 4) continue with xi+1 keeping the rest fixed until minium is reached

But changing one coordinate can affect others, so each coordinate has to be revisited multiple times - so this method is slow, inefficient and limited to small molecules

Derivative methods

Principle = move in direction parallel to the force (first derivative of energy) until minimum of the line

When to stop along the line?

• line search method

• arbitrary step method

These are two different strategies that tell you how far to move along a certain direction once the derivative has told you which way to move.
these are used in other algorithms and are not complete optimization methods themselves

second derivative

minimum = where curvature changes direction

line search method

• 1)start with point 1 with E1 move along direction of the gradient and chooses two now point such that they bracket a minimum (E2<E3)

• 2) fit a parable and compute the minimum= next point

• 3) continue with the new 3 lowest points and repeat until minimum is found

• High accuracy but computationally expensive

difference line search method and sequential univariate method

• Line search method optimizes along derivative guided direction in multidimensional space, (based on cartesion coordinates)

• non derivative sequential univaritate methods only update one paramater at a time (holding others fixed)without derivatives (based on internal coordinates)

during an energy minimization, cartesian coordinates are updated as you move to a low energy conformation, what happens to parameters like bondlenghts, bond angles, strength constants etc.?

During energy minimization, the Cartesian coordinates of atoms are updated to move the system toward a lower-energy conformation. Force field parameters like bond lengths, bond angles, and force constants remain fixed. However, the observed geometric values in the molecule—actual bond lengths, angles, and dihedrals—adjust toward the parameter-defined “ideal” values.

Force field parameters only define ideal values (like bond lengths r0r_0r0​) and how strongly deviations are penalized (force constants). The observed values are the actual bond lengths and angles in the current structure. During minimization, the atoms move to balance all forces, so the observed geometry naturally relaxes toward the ideal values—it emerges from minimizing the total energy, not from the parameters directly.

Arbitrary step approach

• 1) start from initial conformation and compute gradient (direction of steepest descent)

• 2) atomic coordinates are moved along the gradient by a predetermined stepsize

• 3)recompute the gradient

• 4) repeat until no descent in E anymore

• if lambda

  • to big: it overshoots the minimum, so next iteration lower it

  • to small = slow convergence, so next itteration increase its value

• although it may require more itterations than line search method it will always be faster because no repeated E evaluations are done (no optimal lambda)

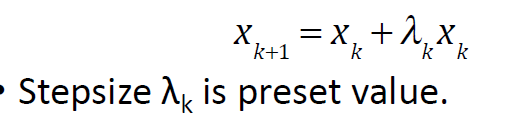
Steepest descent

• 1)Start with an intial structure and calculate the gradient

• 2) move coordinates in this direction of steepest descent by a certain stepsize

  • arbitrary step: fixed

  • line search: optimized every time

• 3) recompute the gradient at the new geometry

  • this itteration will move orthogonal to the previous direction because it now has no component along that direction (if minimization in previous direction is exact with line search, not with aribitrary step)

• 4) repeat until convergence

• simple and good for early stage minimization

• not for final refinement

  • can oscillate in narrow valleys

  • slow convergence near minima due to zig zag behavior

Conjugated gradient

1. start with intial structure and calculate the gradiant

2. move atom coordinates in the direction of the gradient

   1. The first step is a steepest descent

3. Choose a stepsize via line search

   1. usually nog arbitrary step

4. The next step will move in a direction which is a weighted ocmination of the current (orthogonal) gradient and the previous search direction

5. continue unitl convergens

• good for fine tuning

  • higher efficiency because it needs fewer steps to reach the minimum (no zig-zag)

• But more complex because you do a line search at every step