Week 4 Lecture 2 - Finite State Transducers: Moore and Mealy Machines

What is the difference between a finite state transducer (FST) and a deterministic state automaton (DFA)?

When processing an input string, a FST produces an output string rather than a yes/no decision at the end of processing.

It can therefore be thought of as a machine to translate from input strings (from input alphabet) to output strings (from output alphabet).

For an FST M, F_M denotes the function represented by M:

F_M: Σ* → Γ*, where Σ is the input alphabet and Γ is the output alphabet.

Why is an FST (finite state transducer) deterministic?

The output is uniquely determined by the input.

What is a moore machine?

Where are the symbols?

How many symbols does it have?

What is the accepting state?

A type of FST.

They have states emitting output symbols.

One extra symbol is emitted, one symbol more is outputted than there is in the input string

No accepting state, outputs are more inportant than whether a string is accepted.

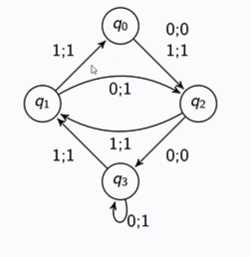
Is this a Moore machine or a Mealy machine, why, and what does it flag?

It is a moore machine because the states have symbols.

It flags a 1 everytime there is an occurance ‘aab’ in a string of ‘a’s and ‘b’s.

Formal definition of a Moore machine (the 6 components).

M = ⟨Q, Σ, Γ, δ, θ, q₀⟩

→ Q, a finite set of states.
→ Σ, the input alphabet.
→ Γ, the output alphabet.
→ δ : Q × Σ → Q, a transition function.
→ θ : Q → Γ, an output function.
→ q₀, an initial state (q0 ∈ Q)

Suppose a moore machine is in state q_i and has input a. If δ(q_i , a) = qj and θ(q_j ) = b, what happens?

The idea is that M will move to state q_j and produce output b.

What is a Mealy machine?

Where are the symbols?

Another type of FST.

The transitions emit output symbols.

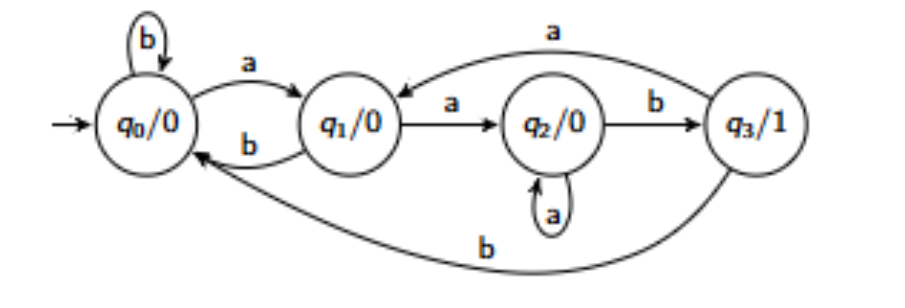
Is this a Moore or Mealy machine, why, and if there is an input of 0110, what would the output be?

This is a mealy machine because the transitions emit output symbols.

If there is an input of 0110, the output would be 1001.

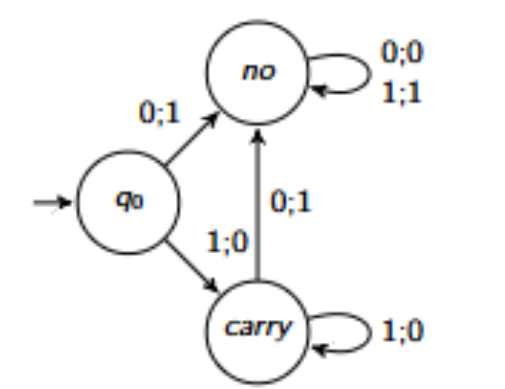
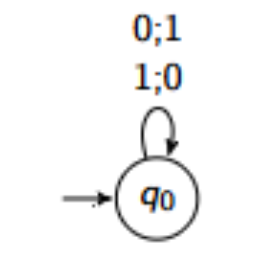
Is this a Moore or Mealy machine, and what does it do?

It is a Mealy machine.

Given k-bit binary numbers n, output k-bit binary numbers corresponding to n+1 (increment). The overflow is ignored.

Formal definition of a Mealy machine (the 6 components).

M = ⟨Q, Σ, Γ, δ, θ, q₀⟩

→ Q, a finite set of states.
→ Σ, the input alphabet.
→ Γ, the output alphabet.
→ δ : Q × Σ → Q, a transition function.
→ θ : Q x Σ → Γ, an output function.
→ q₀, an initial state (q0 ∈ Q)

Suppose a mealy machine is in state q_i and has input a. If δ(q_i , a) = qj and θ(q_j, a) = b, what happens?

The idea is that M will move to state q_j and produce output b.

How to show equivalence of Mealy and Moore machines?

Let Me be a mealy machine and Mo be a moore machine.

Ignore the very first output from the start state because there are no accepting strings.

Equivalent if, for every input string, the output string from Mo is exactly x (the output from the start state) prepended to the output string from Me

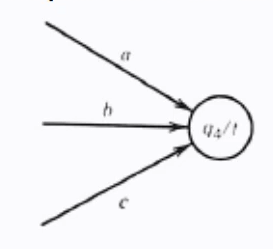
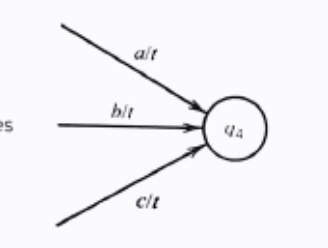
What would be the equivalent Mealy Machine to this Moore Machine?

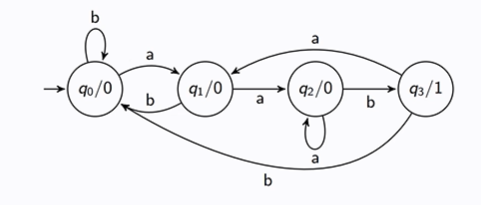
What would be the equivalent Mealy machine to this Moore machine?

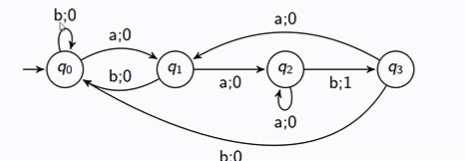
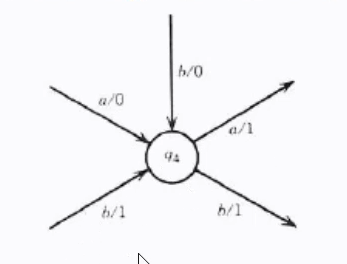
What would be the Moore machine to this Mealy machine?

Can not simply reverse the moore to mealy process because the outputs on the incoming transitions may be different. Need to split the state into 2 or more states based on the outputs on the incoming transitions.

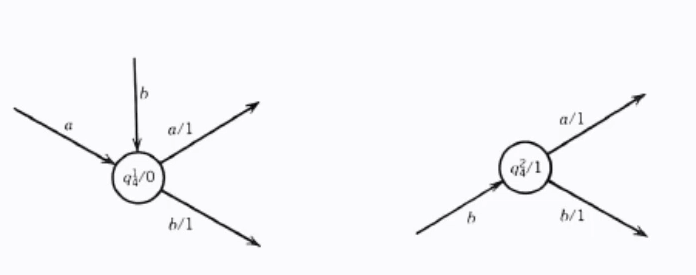
What would be the Moore machine to this Mealy machine?

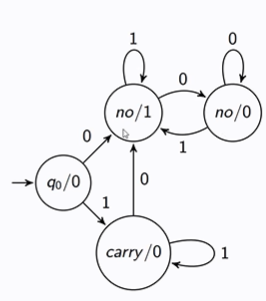
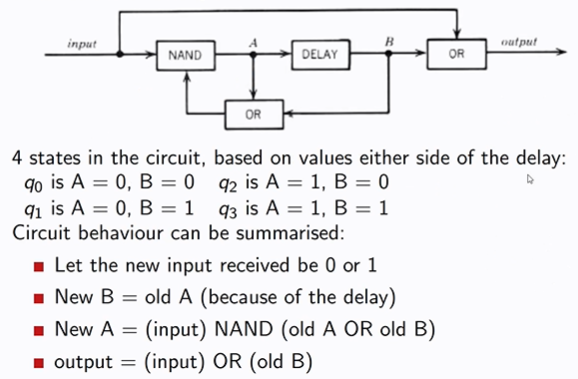
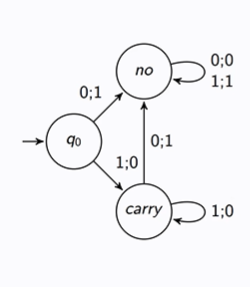
Given this sequential circuit, and the summary of its behaviour, what would be the Mealy machine?