AP Precalculus Review

Exponential function:

If input (x-values) change consistently and output (y-values) values change proportionally

Logarithmic function:

If input (x-values) change proportionally and output (y-values) change consistently

What is the horizontal asymptote in this function: y= 2x²/5x³

Y=0; the denominator power is greater than the numerator power

What is the horizontal asymptote in this function: y= 2x²/5x²

Y=2/5; the powers are equal, leaving the coefficients to be divided

What is the horizontal asymptote in this function: y= 2x³/5x²

None; the numerator power is greater than the denominator power

How do you find a slant asymptote?

Use long division (and disregard the remainder)

Can an equation have a slant and horizontal asymptote?

No

How do you find the equation of a secant line?

Using point-slope formula: y-y1=m(x-x1)

How do you click “RESID” for plots?

Make Ylist: 2nd>STAT>9:RESID

When are functions odd?

f(-x)=-f(x); passes through the origin; SWRT origin

When are functions even?

f(-x)=f(x); symmetric about the y-axis

Arithmetic sequence formula:

an=ak+d(n-k)

Geometric sequence formula:

gn=gk(r )^n-k

When are exponential equations growing?

When a>0, 0<b<1

When are exponential equations decaying?

When a>0, b>1

log(1)/ln(1)=

0

Logb(b)/ln(e)=

1

When do logarithmic functions grow?

When a>0, b>1

When do logarithmic functions decay?

When a>0, 0<b<1

What is a one-to-one function? Can it have an inverse?

When each output has exactly one input; yes

On a semi-log plot, an exponential model will appear ______________ when y-axis is logarithmically scaled

Linear

Where does a sine graph start?

Midline

Where does cosine graph start?

Maximum or minimum

Sine (sin) →

Cosecant (csc)

Cosine (cos) →

Secant (sec)

Tangent (tan) →

Cotangent (cot)

Where are trig functions positive?

QI: All (all)

QII: Students (sin, csc)

QIII: Take (tan, cot)

QIV: Calculus (cos, sec)

Reciprocal identities: sin(x) x csc(x)=

1 (because they’re each others reciprocal)

Reciprocal identities: cos(x) x sec(x)=

1 (because they’re each others reciprocal)

Pythagorean identities:

Think pythagorean equasion (a²+b²=c²)

Pythagorean identities: sin²x+cos²x=

1 (because of unit circle)

Pythagorean identities: 1+tan²x=

sec²x

Pythagorean identities: cot²x+1=

csc²x

Double angle identities:

When trigonometric functions has a 2x

Double angle identities: sin(2x)=

2sin(x) x cos(x)

Double angle identities: cos(2x)=

cos²x-sin²x

2cos²x-1

1-2sin²x

Sum/difference formulas:

Think sin=same sign; cos=different sign

Sum formulas: sin(A+B)=

(sinA)(cosB)+(cosA)(sinB)

Sum formulas: cos(A+B)=

(cosA)(cosB)-(sinA)(sinB)

Sine sum/difference formulas:

Sin and cos on both sides (sin goes first)

Cos sum/difference formulas:

Cos and sin together on both sides (cos goes first)

Difference formulas: sin(A-B)=

(sinA)(cosB)-(cosA)(sinB)

Difference formulas: cos(A-B)=

(cosA)(cosB)+(sinA)(sinB)

How do you solve for the phase shift in a sin function using start?

Equation: B(x+C)=0

FRQ 3: Go to the first midline point graphed, and plug x in

Solve for C

How do you solve for the phase shift in a cos function using maximum?

Equation: B(x+C)=0

FRQ 3: Go to the first maximum point graphed, and plug x in

Solve for C

Y=Asinx/cosx(B(x+C))+D

A=amplitude

B=number of cycles (P=2π/B)

C=phase shift

D=midline

How do you change from polar coordinates to rectangular coordinates?

x=rcosθ

y=rsinθ

How do you change from rectangular to polar coordinates?

x²+y²=r²

tanθ=y/x

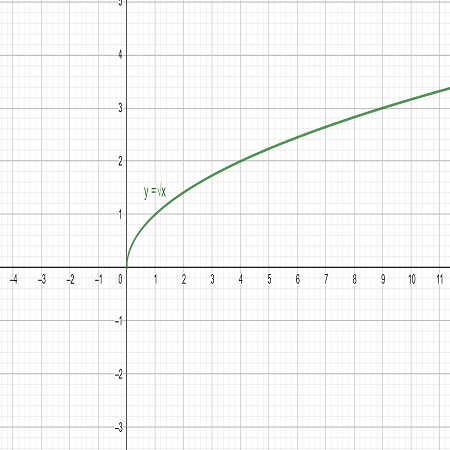
Y=√x

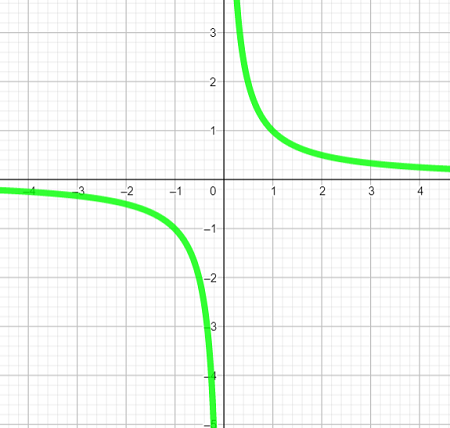
Y=1/x

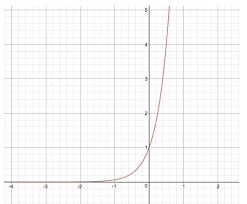
Y=2^x

Y=logx

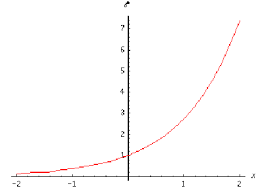
Y=e^x

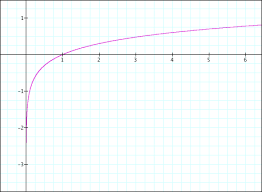
Y=lnx

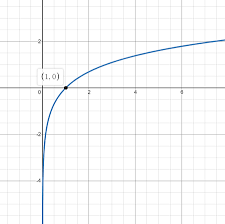
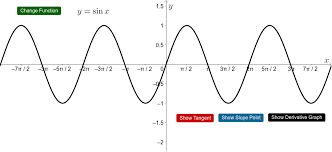
Y=sinx

Y=cosx

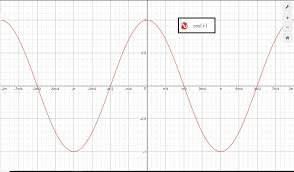
Y=tanx

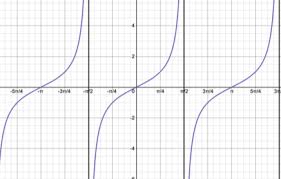
Y=cscx

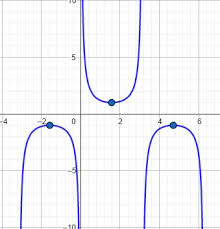
Y=secx

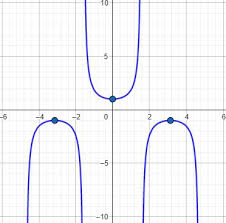
Y=cotx

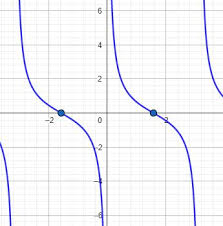
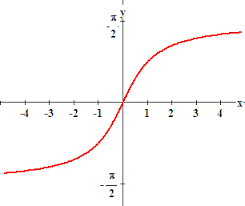
Y=sin^-1x

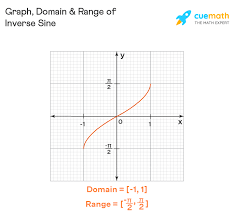
Y=cos^-1x

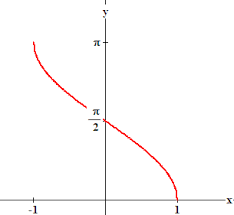
Y=tan^-1x