direct chaining

direct chaining

= a chaining strategy

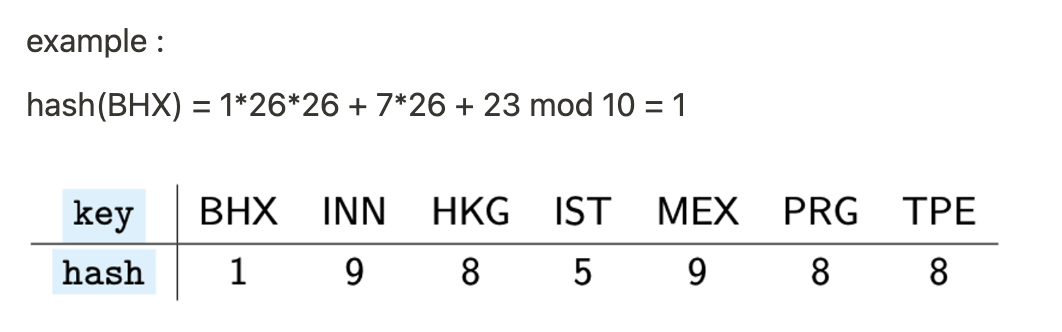
example

entries: airport codes e.g. BHX, INN, HKG, IST…

table size: 10

hash function:

• we treat the codes as a no in base 26 (A = 0, B=1, …, Z= 25)

  example: ABC = 0×26×2 + 1×26 + 2 = 28

• hashcode is computed mod 10 (to make sure that the index is 0, 1, 2, 3, … or 9)

example (see pic):

hash(BHX) = 1×26×26 + 7×26 + 23 mod 10 = 1

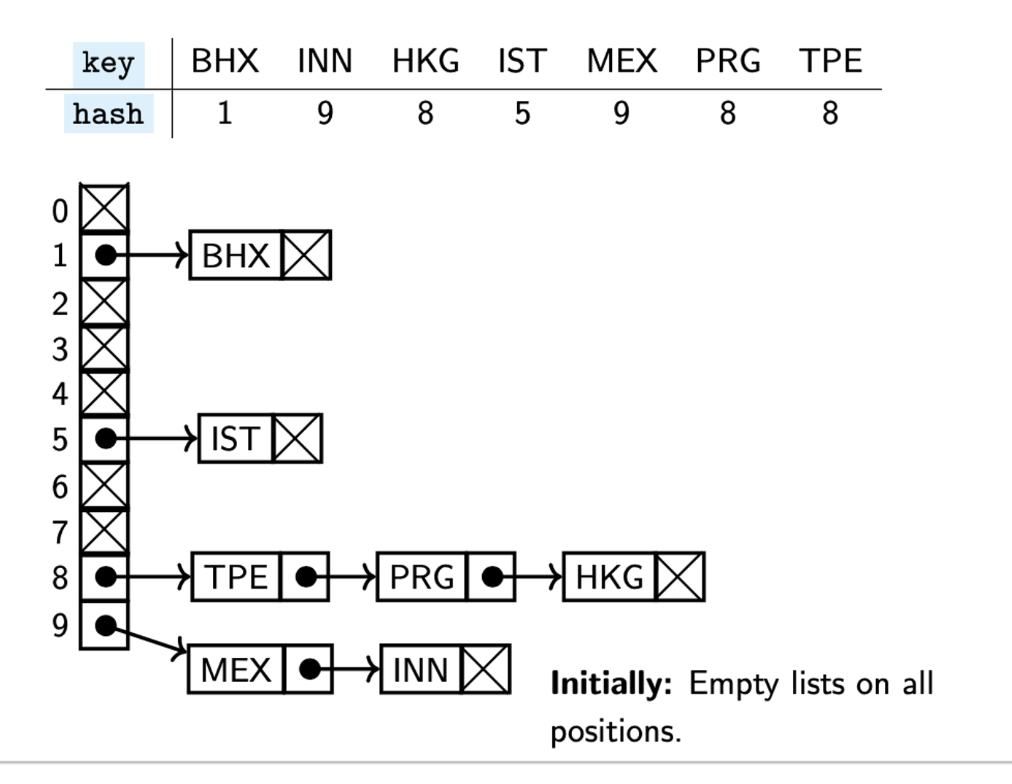
cont

to insert, always 1st check if the key we’re inserting is in the linked list on position hash(key). if it isn’t, we insert the key at the beginning of that list

• (we’re inserting without duplicates)

to delete(key) we delete key from the l.l. stored on position hash(key), if it is there. Similarly, lookup(key) returns true/false depending on if key is stored in the list on position hash(key)

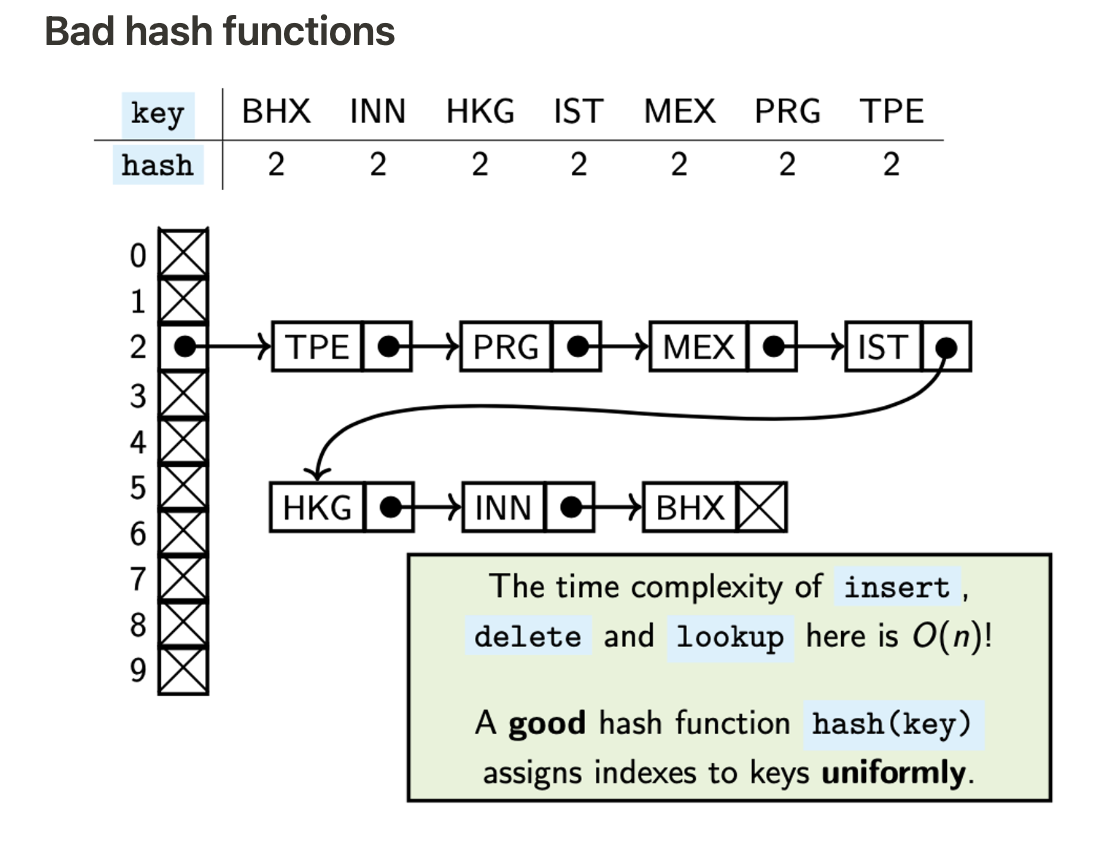
bad hash functions

the hash function assigns 2 to all keys = when inserting a new key, 1st check if key is stored in the linked list on position hash(key)=2.

• this requires to go through all the elements alr stored in the hash table = O(n) time complexity

similarly, lookup + delete are also O(n)

to tackle = need a good hash function which uniformly distributes the keys among positions aka, given a random key, it out to have the same probability of being stored on every position

time complexity of direct chaining part 1

load factor of hash table = avg no of entries stored on a location

good hash function = a location given by hash(key) has the expected no of entries stored there equal to n/T

unsuccessful lookup of key:

• key is not in the table

• location hash(key) stores n/T entries, on average

  = we have to traverse them all

load factor = how full hash table is, good hash function, the load factor 0.25 represents 25% of getting a collision

• consequence of good hash function = the l.l. on position hash(key) , for a randomly selected key, has expected length n/T

“expected” = the list stored on position hash(key)might be longer, it might be shorter, but it’s length will most likely be approximately n/T (for a randomly selected key )

time complexity of direct chaining pt 2

time complexity pt 3

to summarise

we made 2 assumptions:

1. we have a good hash function

2. we assume a max load factor

consequence of 1st assumption = the expected length of chains is n/T and the 2nd = n/T ≤ λ, for some fixed constant number λ

by assuming those 2 conditions, we have computed that the operations of hash tables are all in O(1)

whether hash function = good depends on distribution of data, on the other hand, making sure that the load factor is bounded by some λ can be done automatically

• the consequence of our approach will be that the constant time complexity will be (only) amortised

disadvantage of chaining strategies

1. typically, alot of hash collisions = alot of unused space

2. linked lists require a lot of allocations (allocate_memory) which is slow

2 open addressing strategies which avoid those problems: linear probing + double hashing…..