Honors Algebra 1 Review - 9th Grade Math Placement Test

9

Find the value of c that makes x²+6x+c a perfect square trinomial

4

Find the value of c that makes x²+4x+c a perfect square trinomial

49

Find the value of c that makes x²-14x+c a perfect square trinomial

1

Find the value of c that makes x²-2x+c a perfect square trinomial

81

Find the value of c that makes x²-18x+c a perfect square trinomial

100

Find the value of c that makes x²+20x+c a perfect square trinomial

6.25

Find the value of c that makes x²+5x+c a perfect square trinomial

1225

Find the value of c that makes x²-70x+c a perfect square trinomial

30.25

Find the value of c that makes x²-11x+c a perfect square trinomial

20.25

Find the value of c that makes x²+9x+c a perfect square trinomial

{2, -6}

Solve by completing the square. Round to the nearest tenth if necessary: x²+4x-12=0

{3, 5}

Solve by completing the square. Round to the nearest tenth if necessary: x²-8x+15

{-7, 1}

Solve by completing the square. Round to the nearest tenth if necessary: x²+6x=7

{-3, 5}

Solve by completing the square. Round to the nearest tenth if necessary: x²-2x=15

{2. 12}

Solve by completing the square. Round to the nearest tenth if necessary: x²-14x+30=6

{-11, -1}

Solve by completing the square. Round to the nearest tenth if necessary: x²+12x+21=10

{0.3, 3.7}

Solve by completing the square. Round to the nearest tenth if necessary: x²-4x+1=0

{0.8, 5.2}

Solve by completing the square. Round to the nearest tenth if necessary: x²-6x+4=0

{1.6, 6.4}

Solve by completing the square. Round to the nearest tenth if necessary: x²-8x+10=0

{-1.4, 3.4}

Solve by completing the square. Round to the nearest tenth if necessary: x²-2x=5

{-9.9, -0.1}

Solve by completing the square. Round to the nearest tenth if necessary: 2x²+20x=-2

f(x) = |x|

What is the function of this graph?

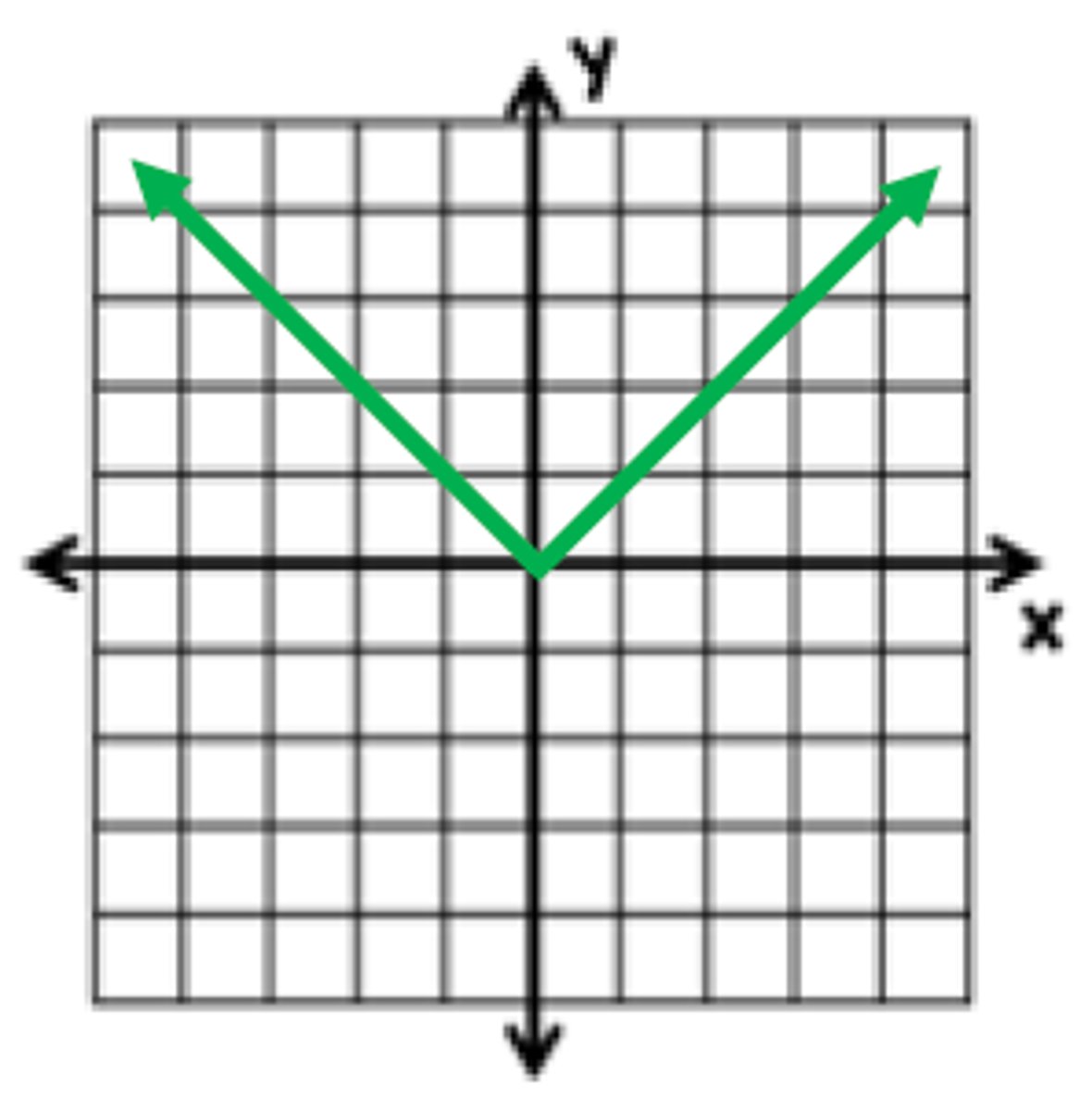
f(x) = |x| + 2

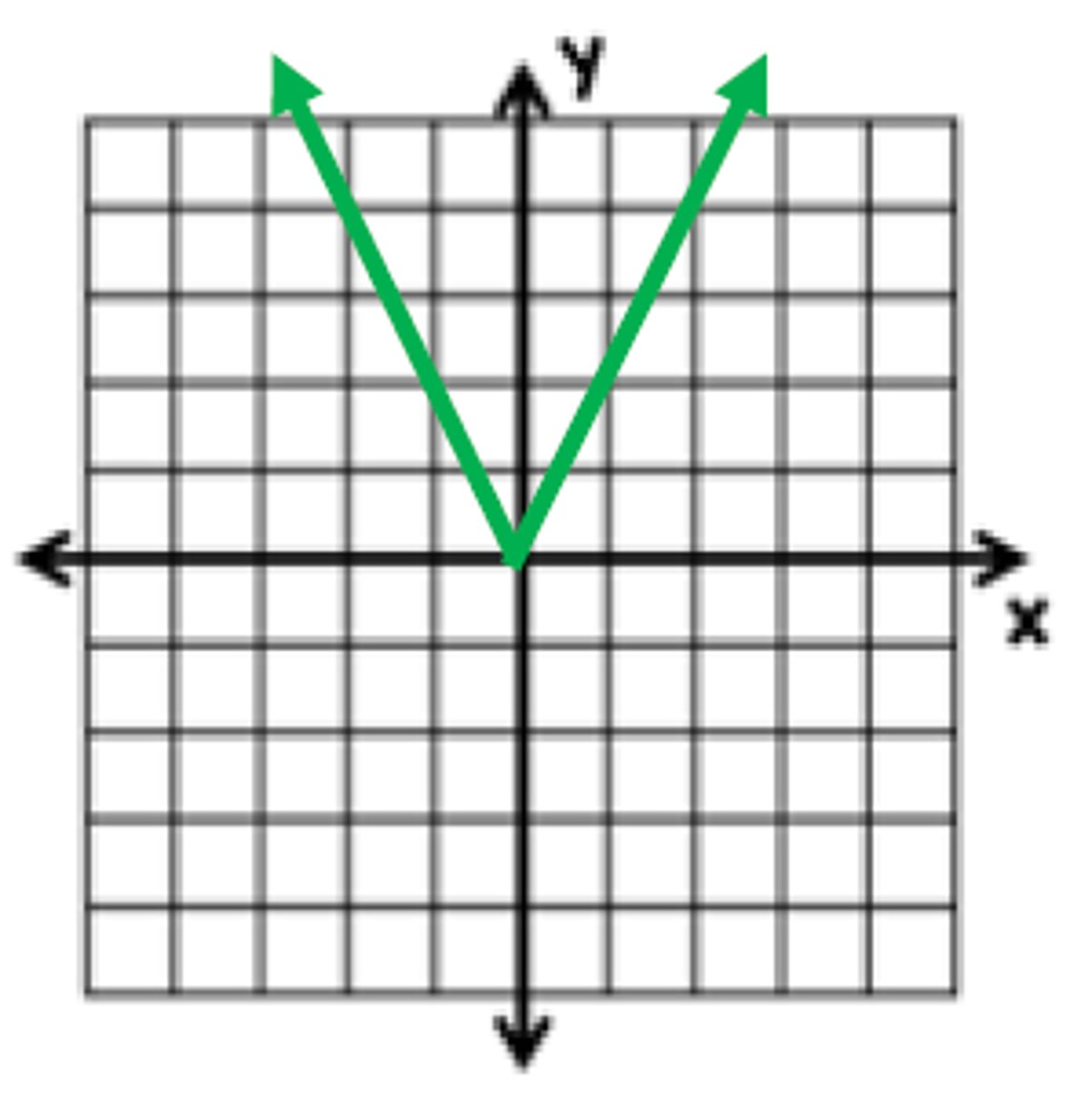
What is the function of this graph?

f(x) = 2|x|

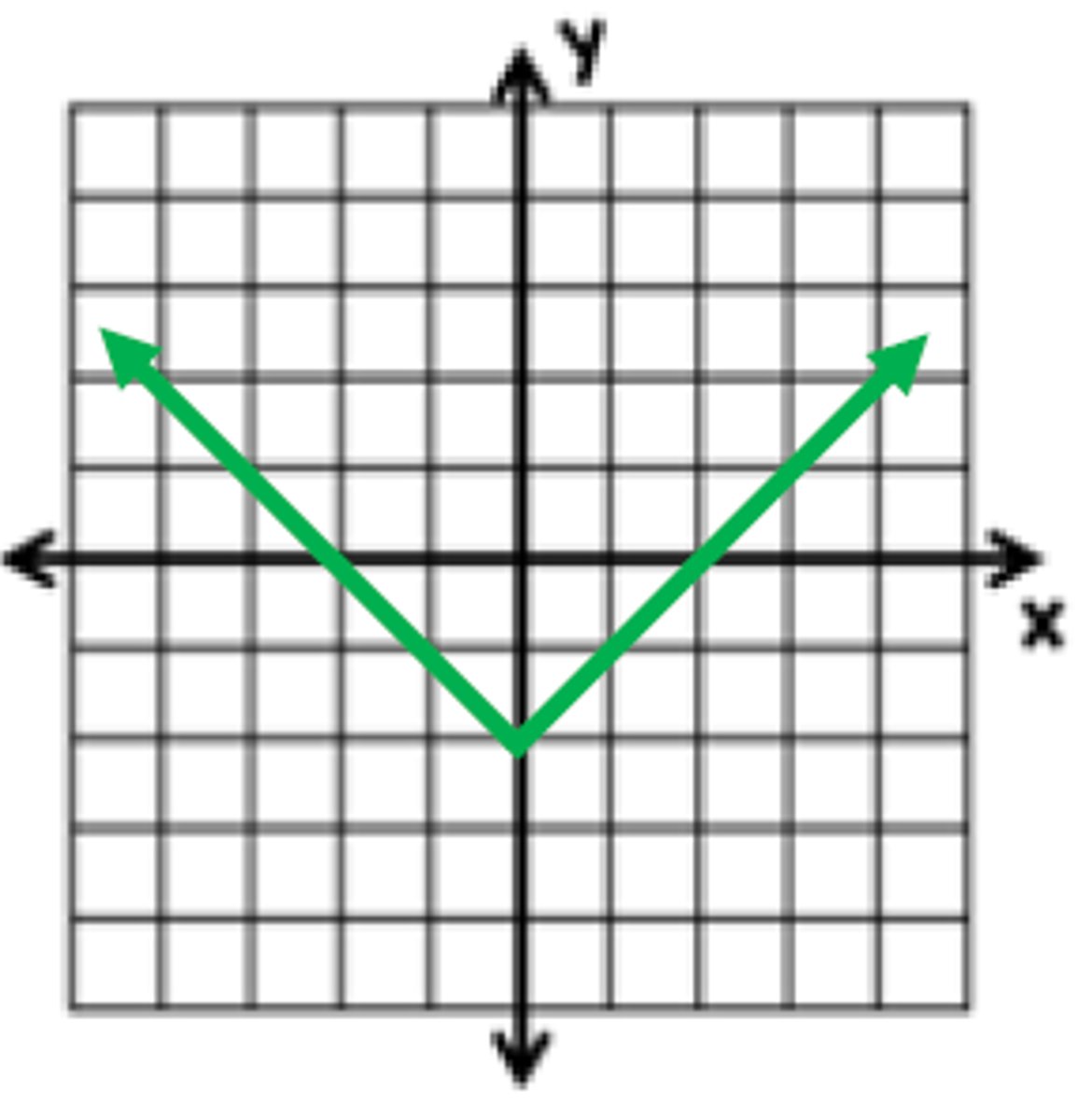
What is the function of this graph?

f(x) = |x| - 2

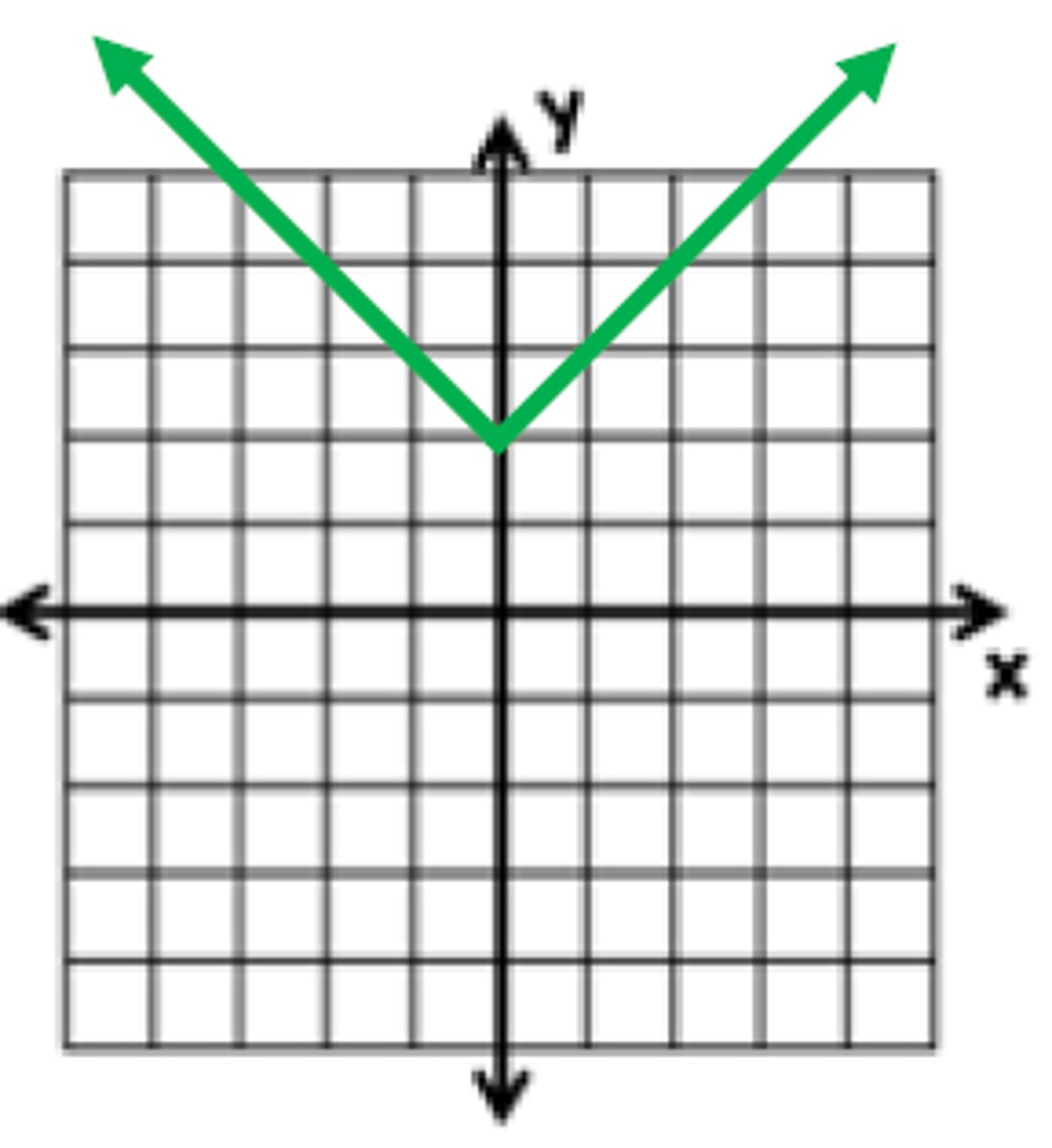
What is the function of this graph?

f(x) = |x - 2| + 1

What is the function of this graph?

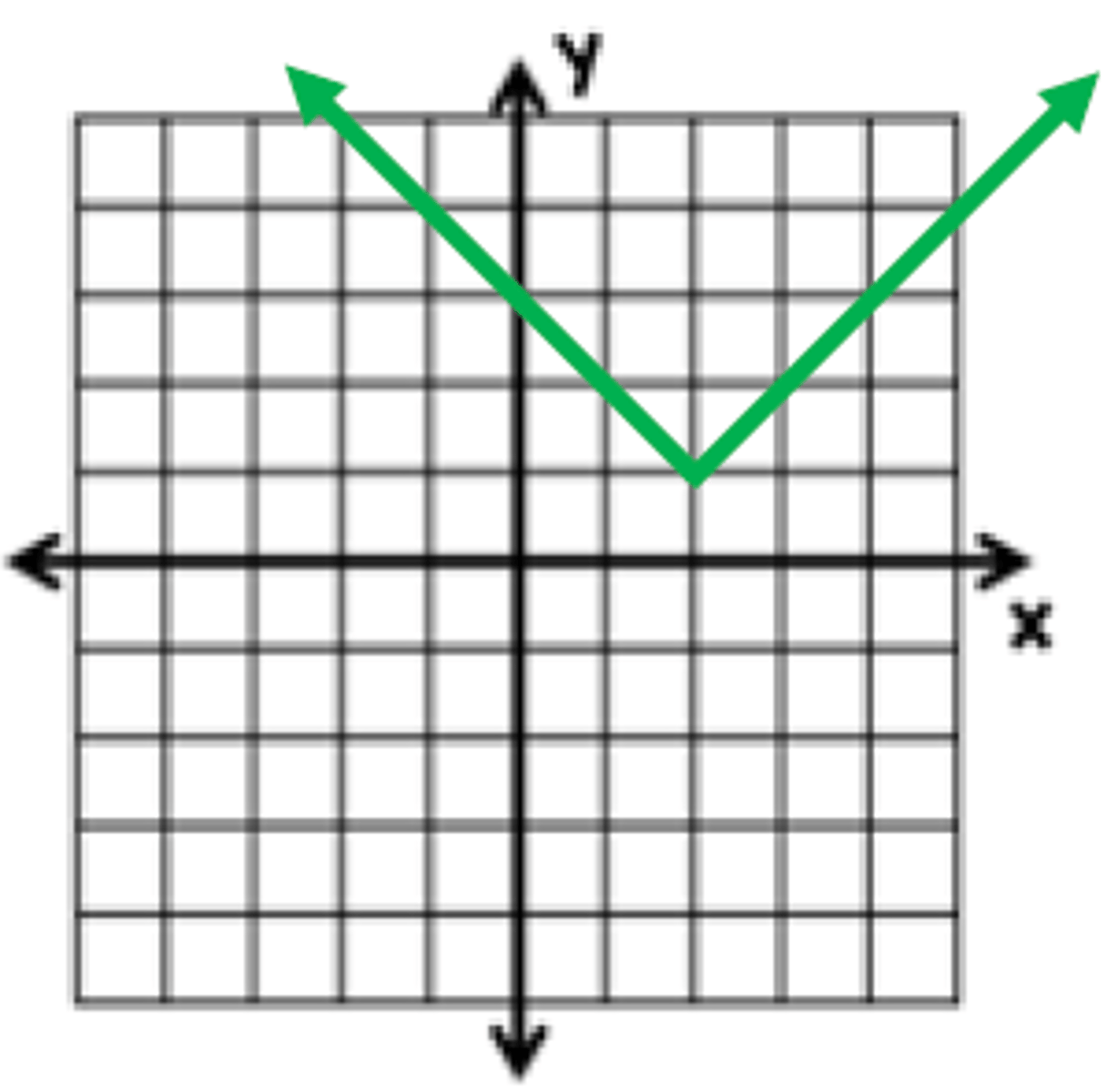
f(x) = |x - 3| - 1

What is the function of this graph?

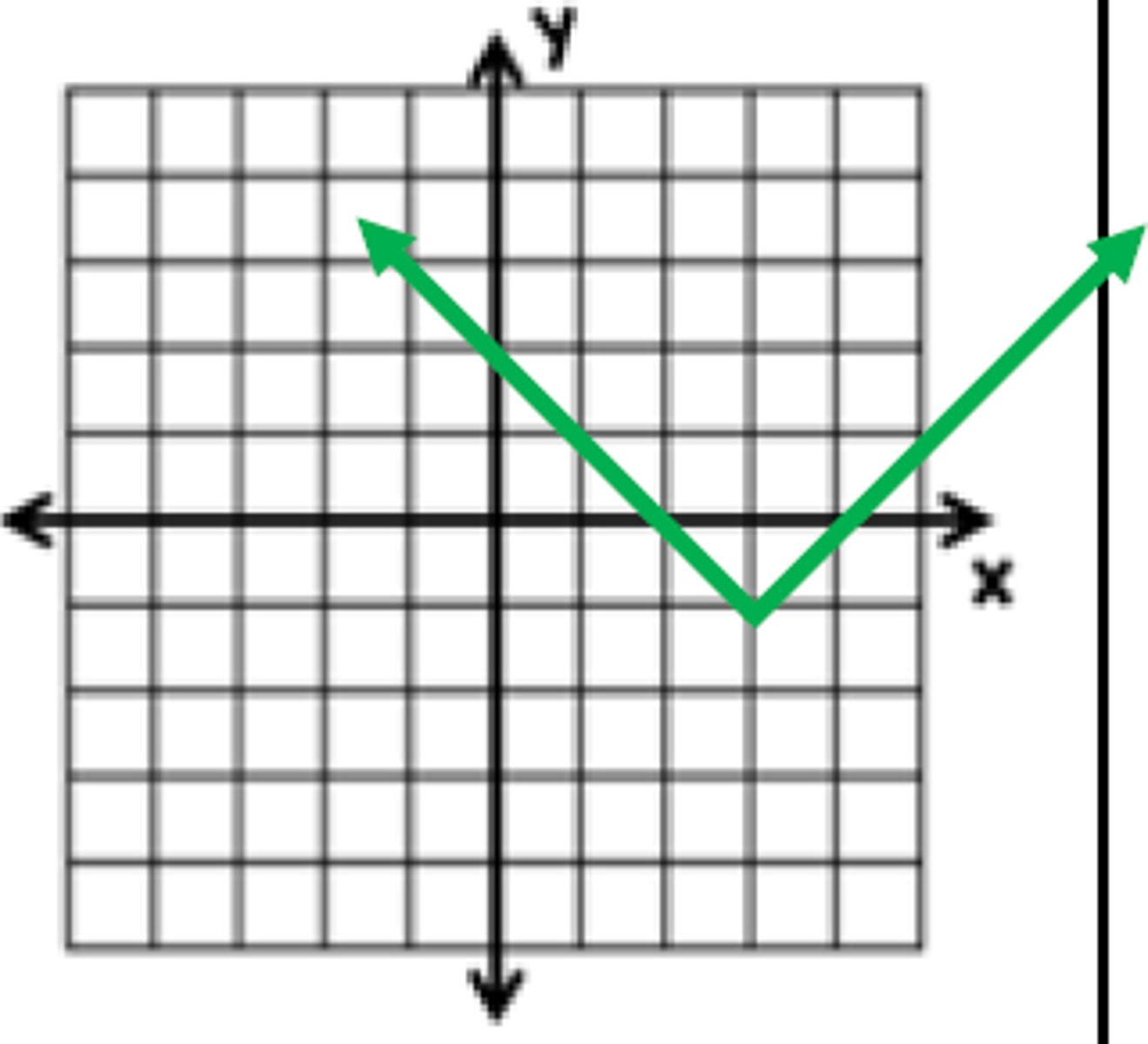
(0, 0)

What is the vertex of: f(x) = |x|

(0, -4)

What is the vertex of: f(x) = |x| - 4

(4, 0)

What is the vertex of: f(x) = |x - 4|

(2, 0)

What is the vertex of: f(x) = |x - 2|

(0, -2)

What is the vertex of: f(x) = |x| - 2

(4, 5)

What is the vertex of: f(x) = |x - 4| + 5

(5, 4)

What is the vertex of: f(x) = |x - 5| + 4

(-4, 5)

What is the vertex of: f(x) = |x + 4| + 5

(4, -5)

What is the vertex of: f(x) = |x - 4| - 5

(5, -4)

What is the vertex of: f(x) = |x - 5| - 4

narrow graph

Does f(x) = 2|x| have a narrow or wide graph?

wide graph

Does f(x) = 0.5|x| have a narrow or wide graph?

narrow graph

Does f(x) = 3|x| have a narrow or wide graph?

wide graph

Does f(x) = 0.25|x| have a narrow or wide graph?

Axis of Symmetry

The line that splits a quadratic equation at the point of symmetry is called

a

In the expression ax² + bx + c, which value determines how the parabola opens?

Vertex

What is the point at which the parabola begins to change direction?

Minimum

If a quadratic equation opens upward, is the vertex a maximum or minimum?

x

Is the axis of symmetry the x value of the vertex or the y value of the vertex

1

How many roots / solutions does a quadratic equation have if the vertex is on the x-axis?

0 or No real solution

How many roots / solutions does a quadratic equation that opens up with a vertex of (2, 4) have?

2

How many roots / solutions does a quadratic equation that opens down with a vertex of (2, 4) have?

Create an x / y table.

When graphing a quadratic equation, what is the step that follows finding the vertex?

x = 2

What is the axis of symmetry for the quadratic equation x² - 4x + 6 = 0?

(2, 2)

What is the vertex for the quadratic equation x² - 4x + 6 = 0?

Minimum

Is the vertex for the quadratic equation x² - 4x + 6 = 0 a max or a min?

x = 0

What is the axis of symmetry for the quadratic equation y = x² + 2?

(0, 2)

What is the vertex for the quadratic equation y = x² + 2?

Down

Will the graph for the quadratic equation f(x) = -2x² + 8x - 3 open up or down?

x = -2

What is the axis of symmetry in the graph shown?

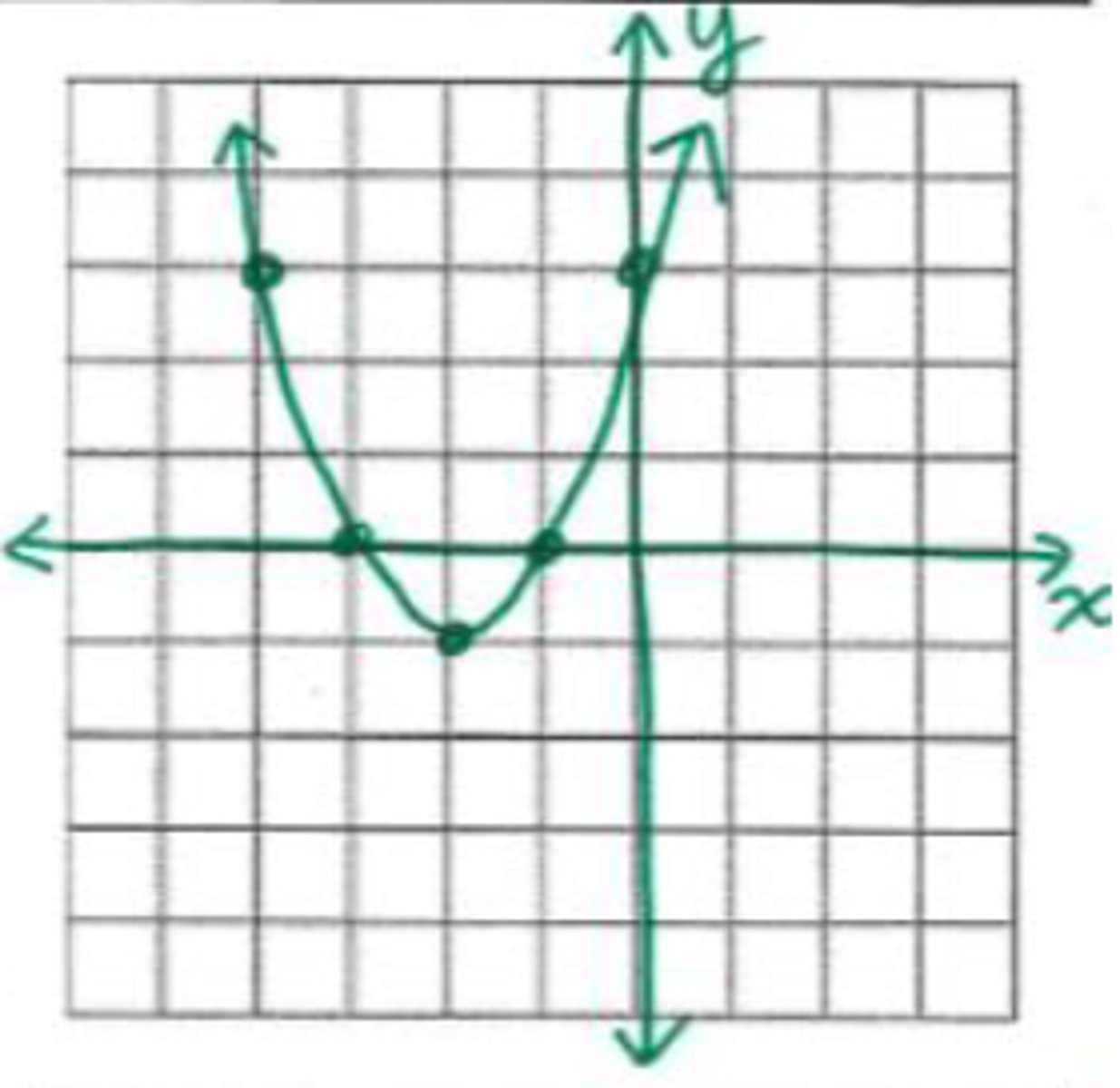
(-2, -1)

What is the vertex in the graph shown?

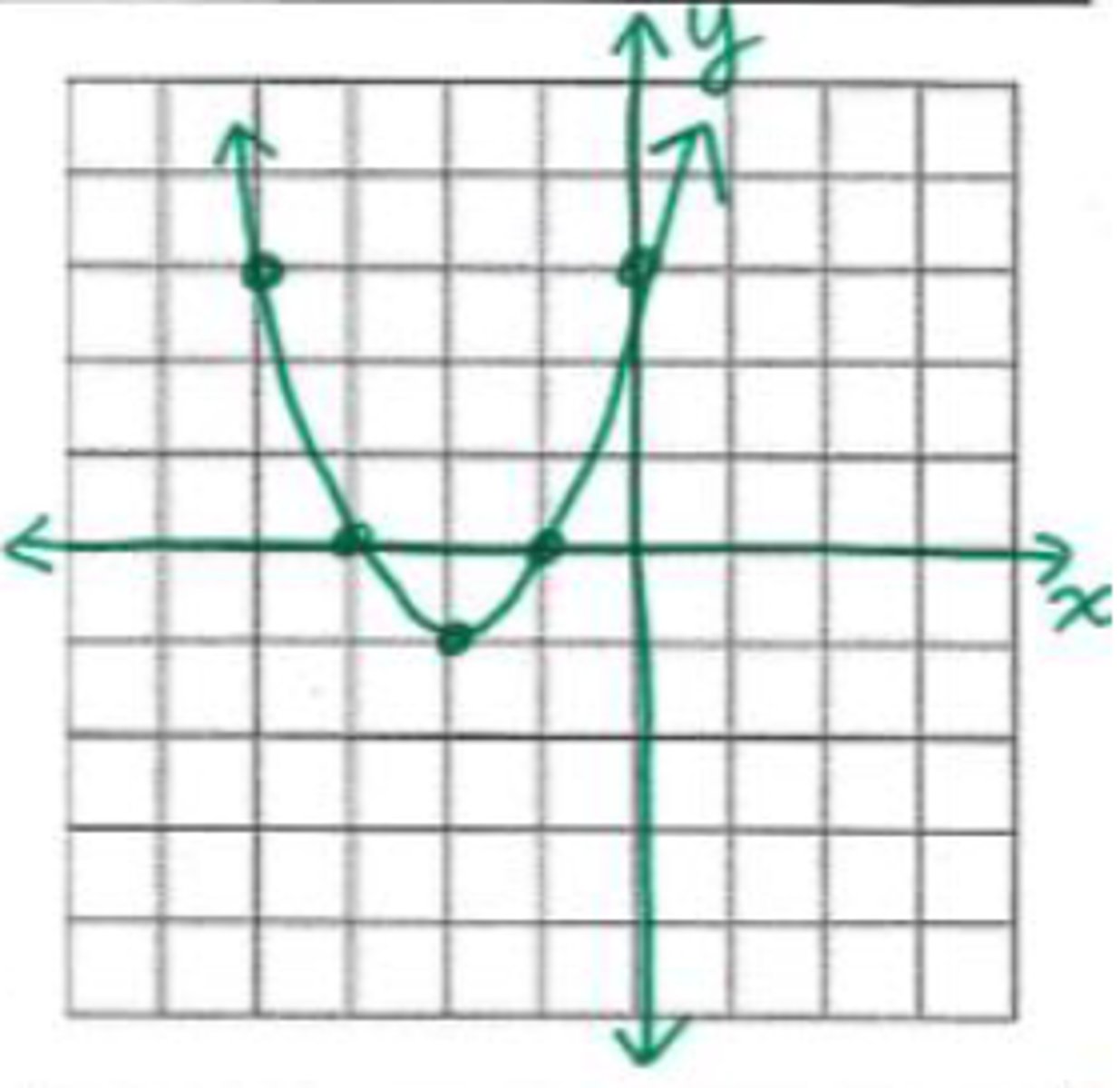
domain: all reals; range: y ≥ -1

What is the domain and range in the graph shown?

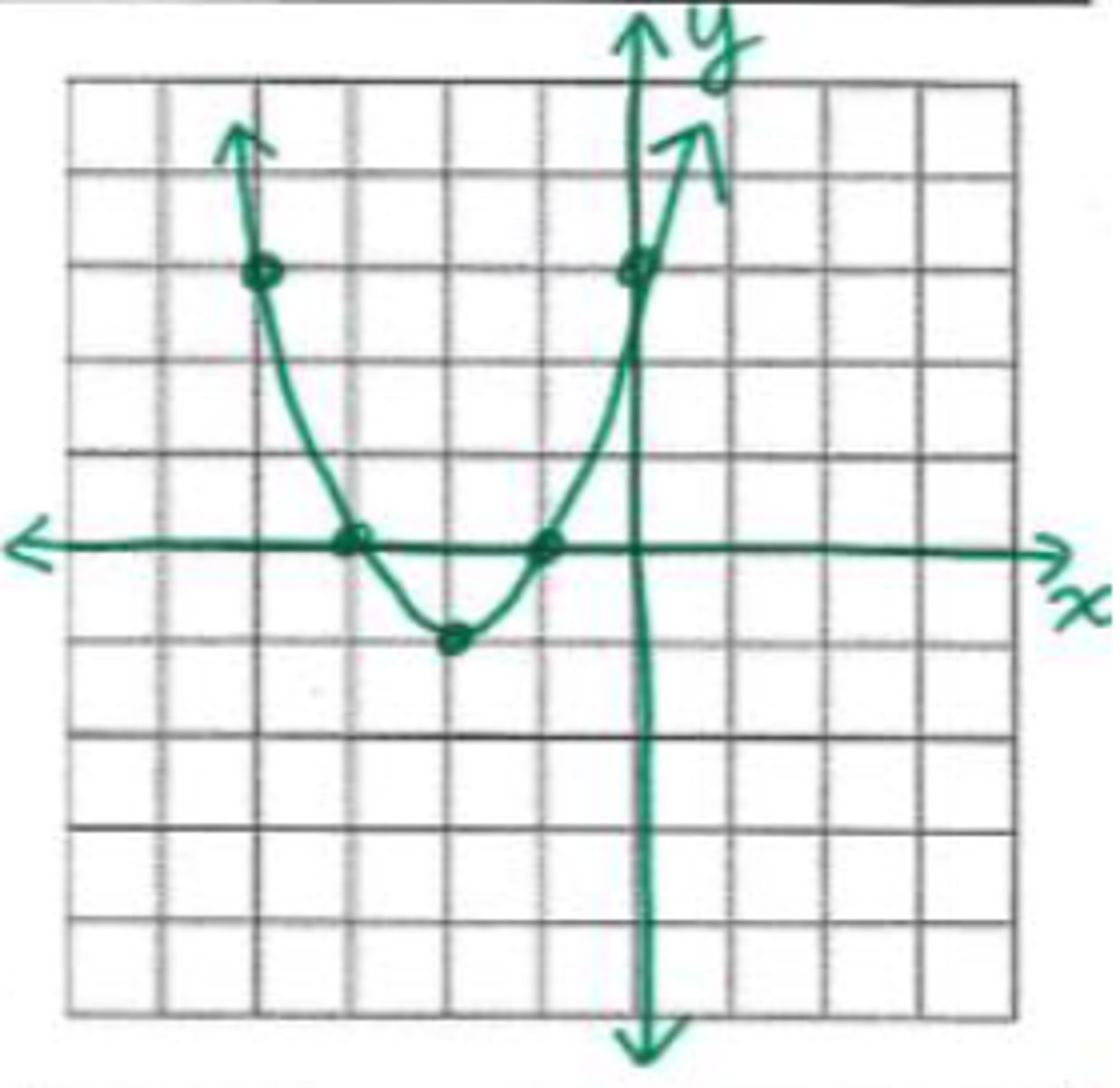
x = {-3, -1}

What are the roots of the graph shown?

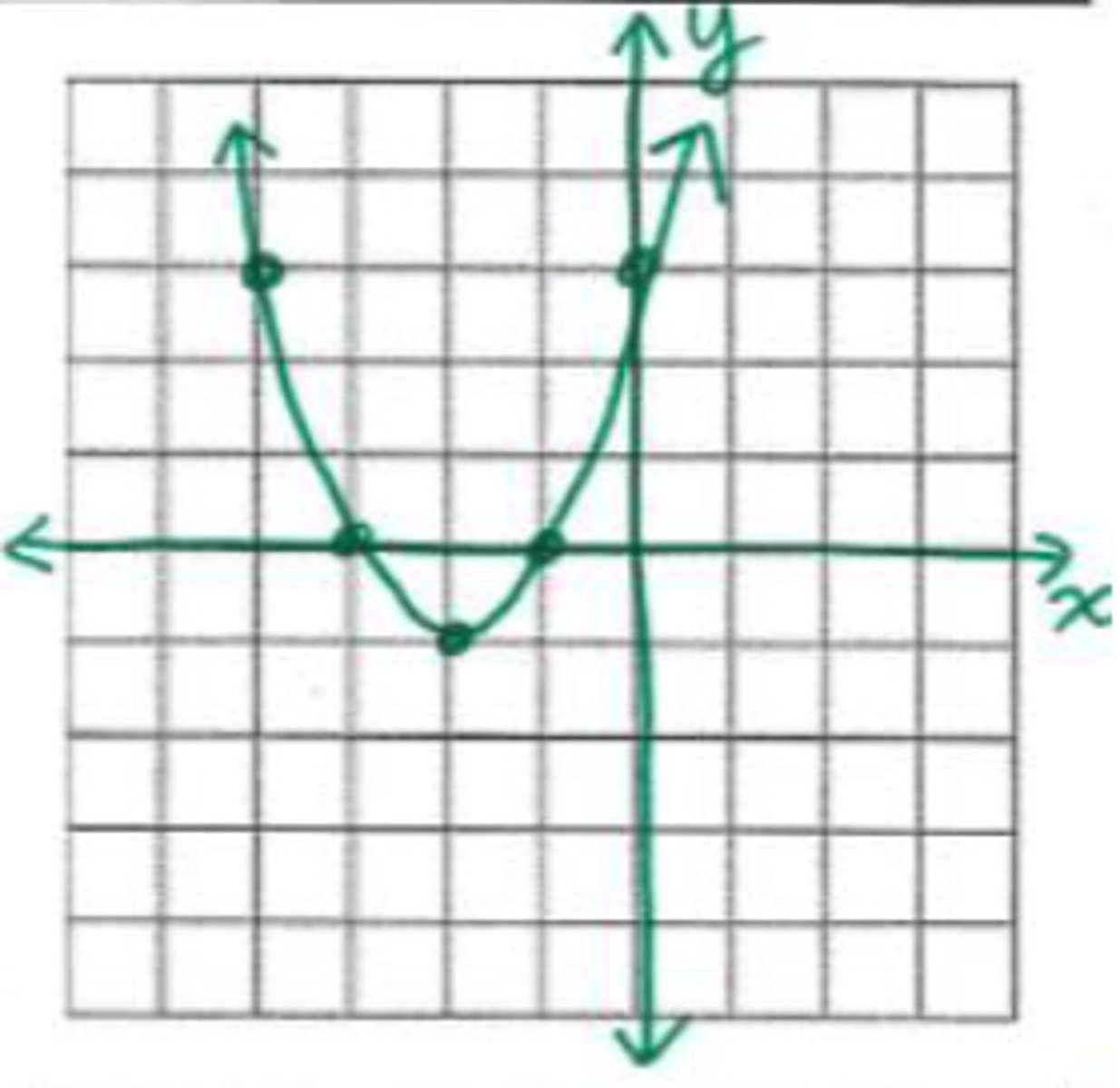
x = 0

What is the axis of symmetry in the graph shown?

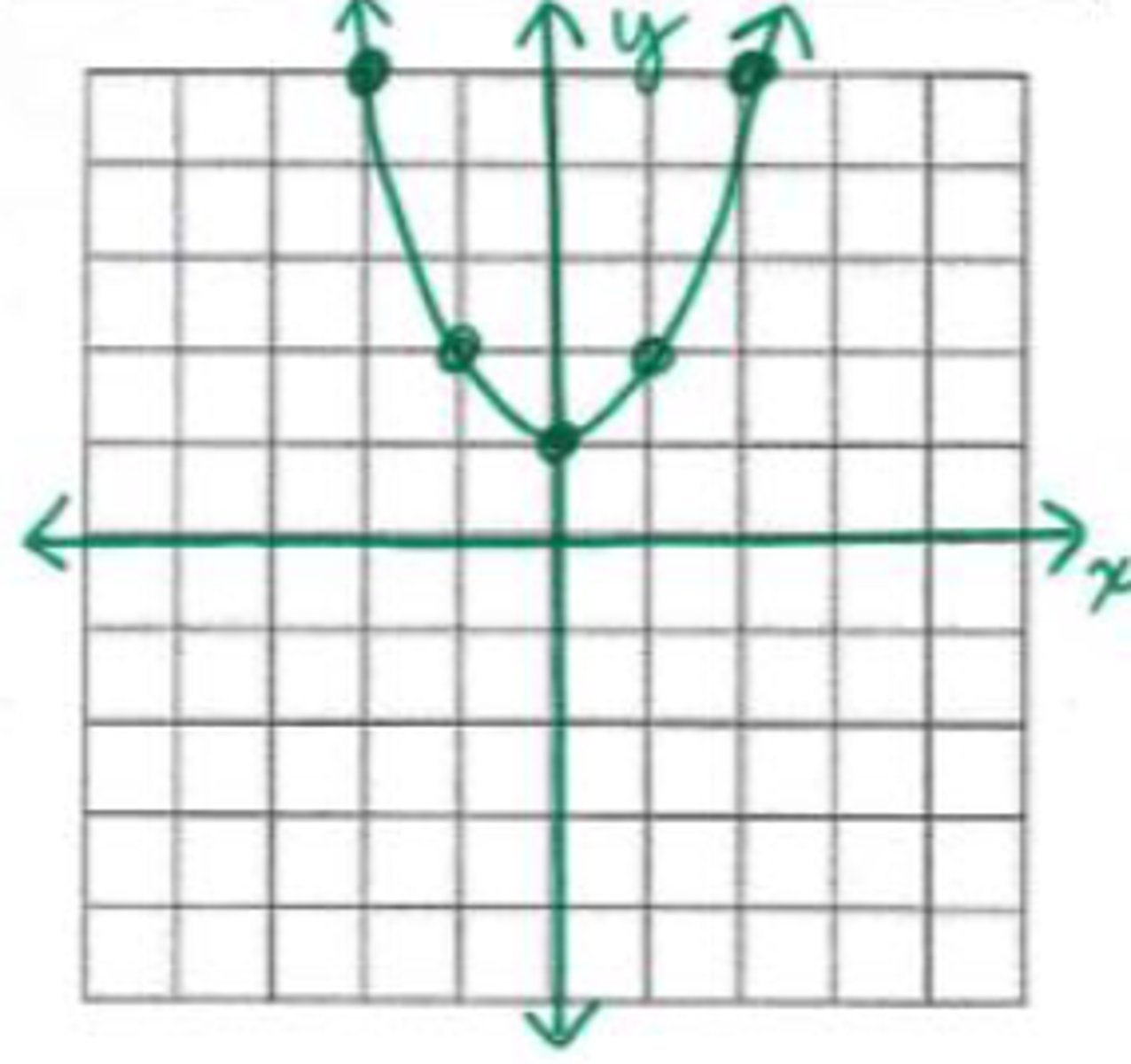
(0, 1)

What is the vertex in the graph shown?

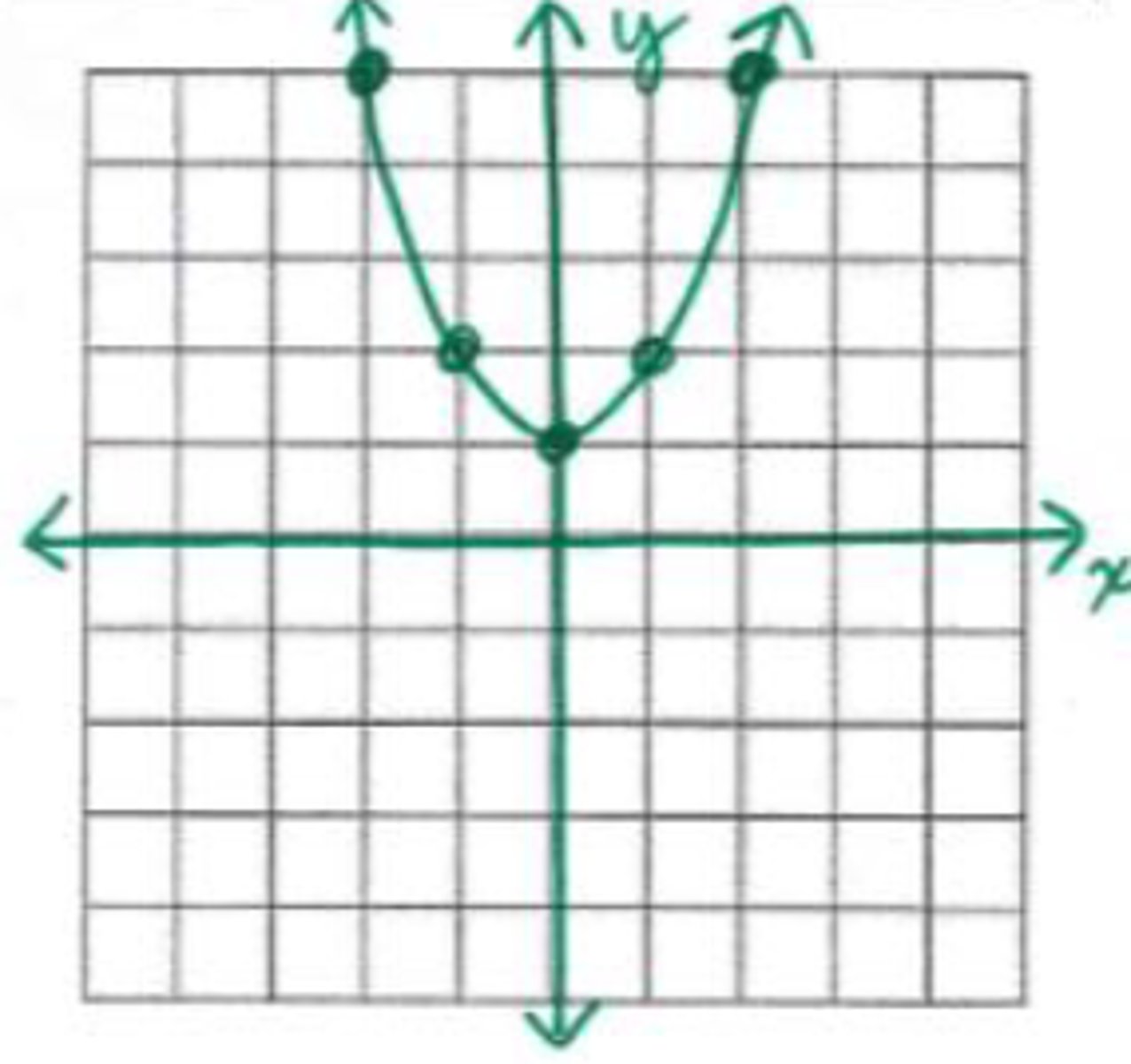
domain: all reals; range: y ≥ 1

What is the domain and range in the graph shown?

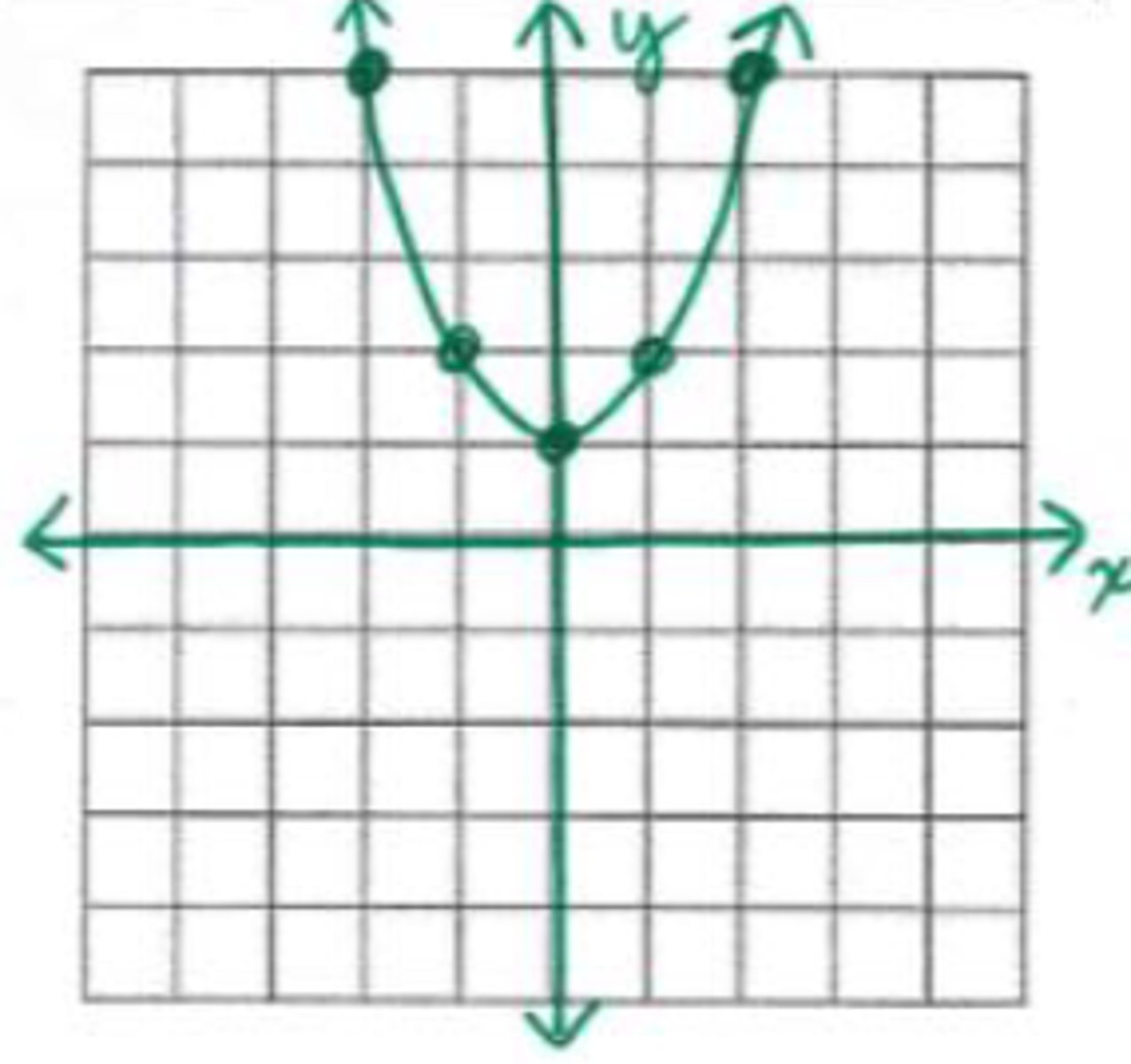
x = {∅} no roots

What are the roots of the graph shown?

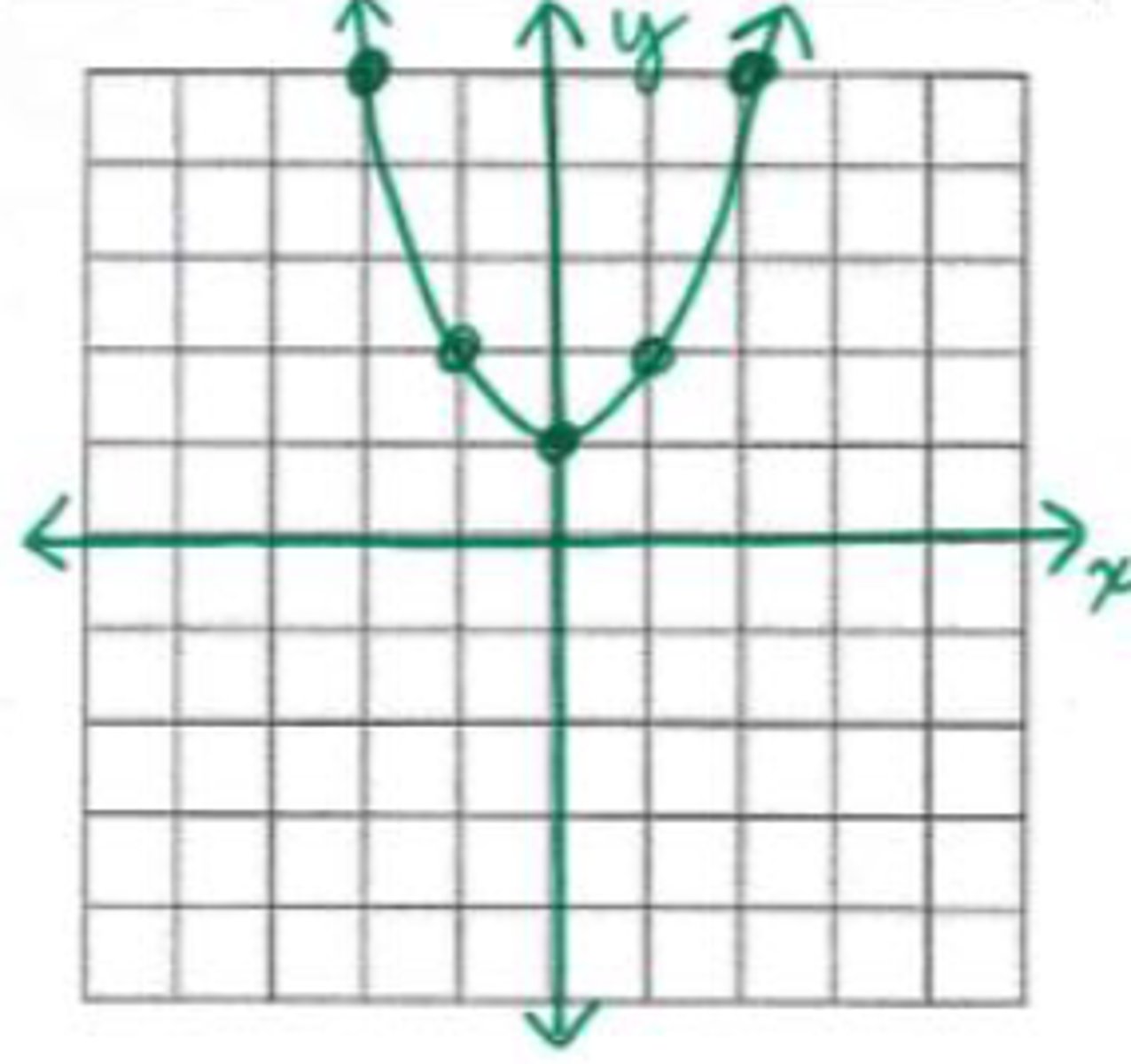
x = -1

What is the axis of symmetry in the graph shown?

(-1, -4)

What is the vertex in the graph shown?

domain: all reals; range: y ≥ -4

What is the domain and range in the graph shown?

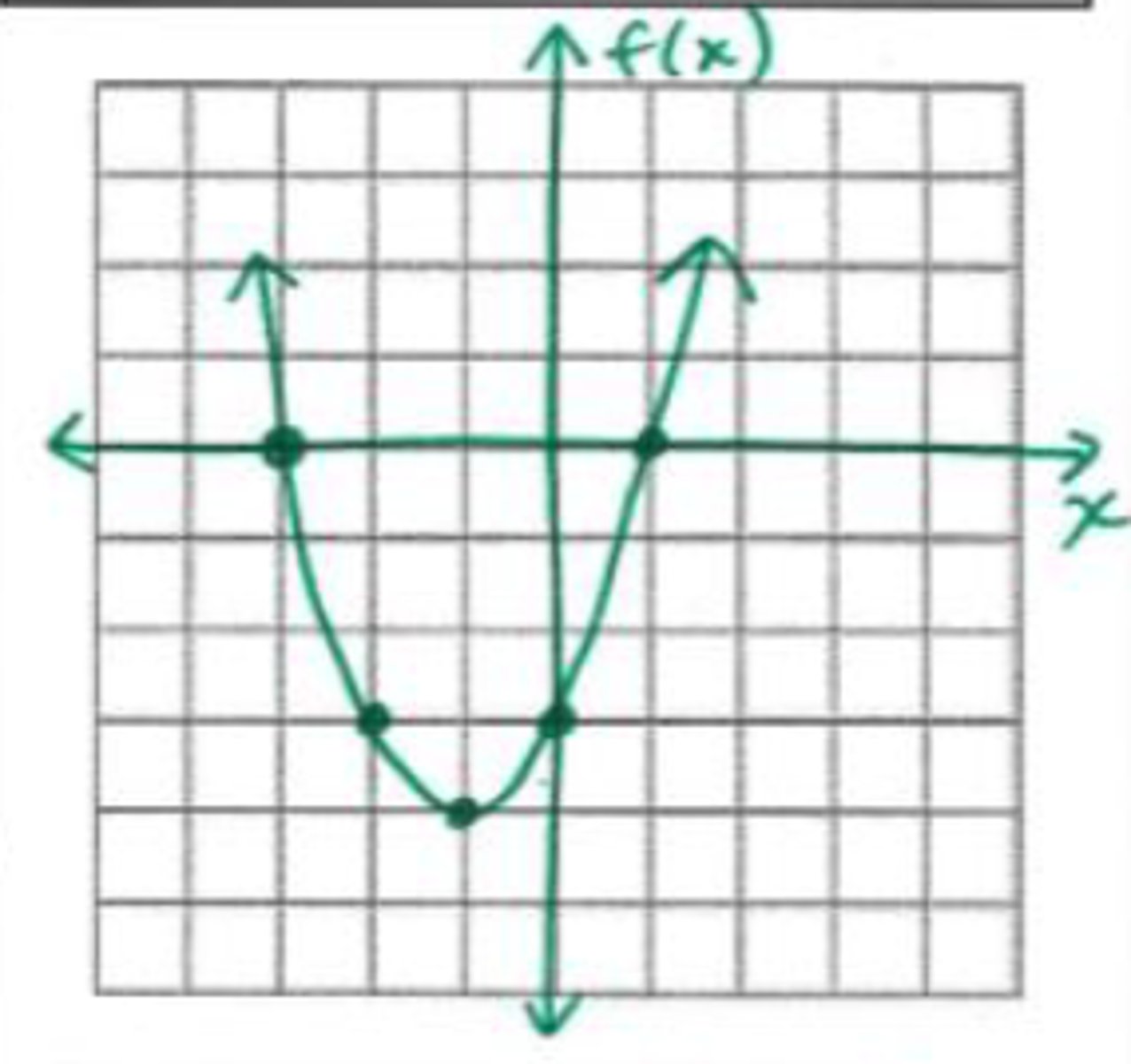
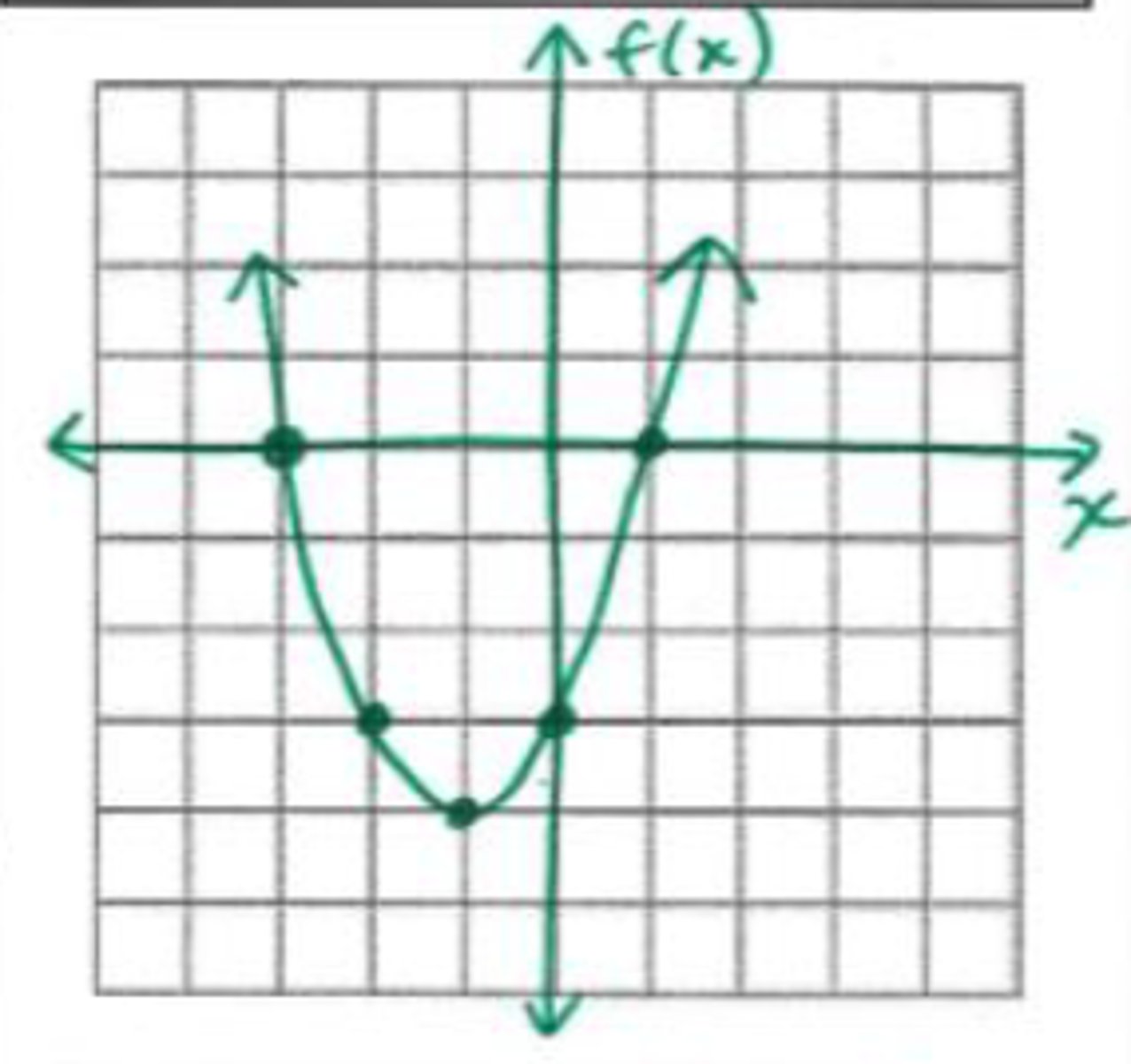
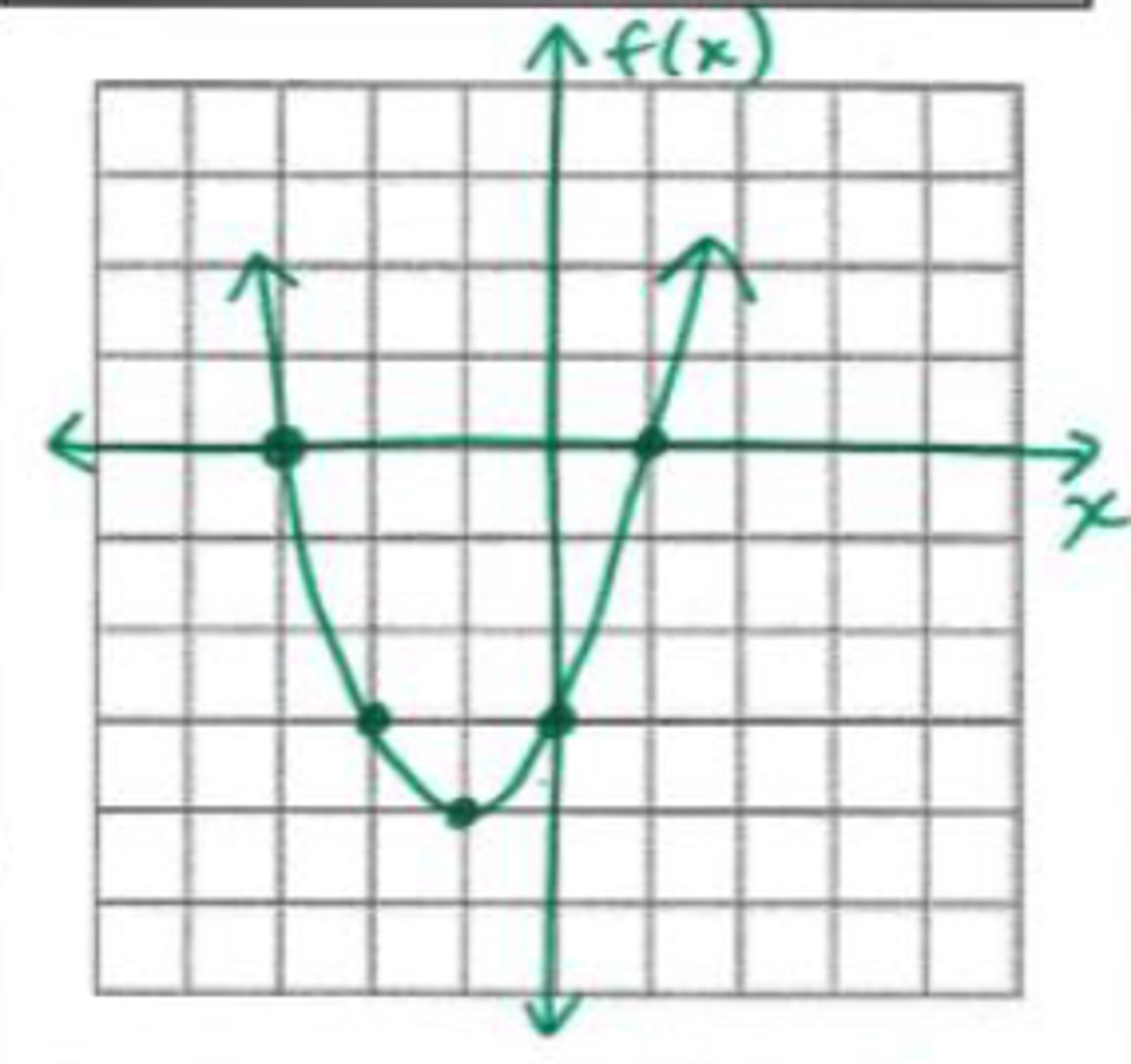
x = {-3, 1}

What are the roots of the graph shown?

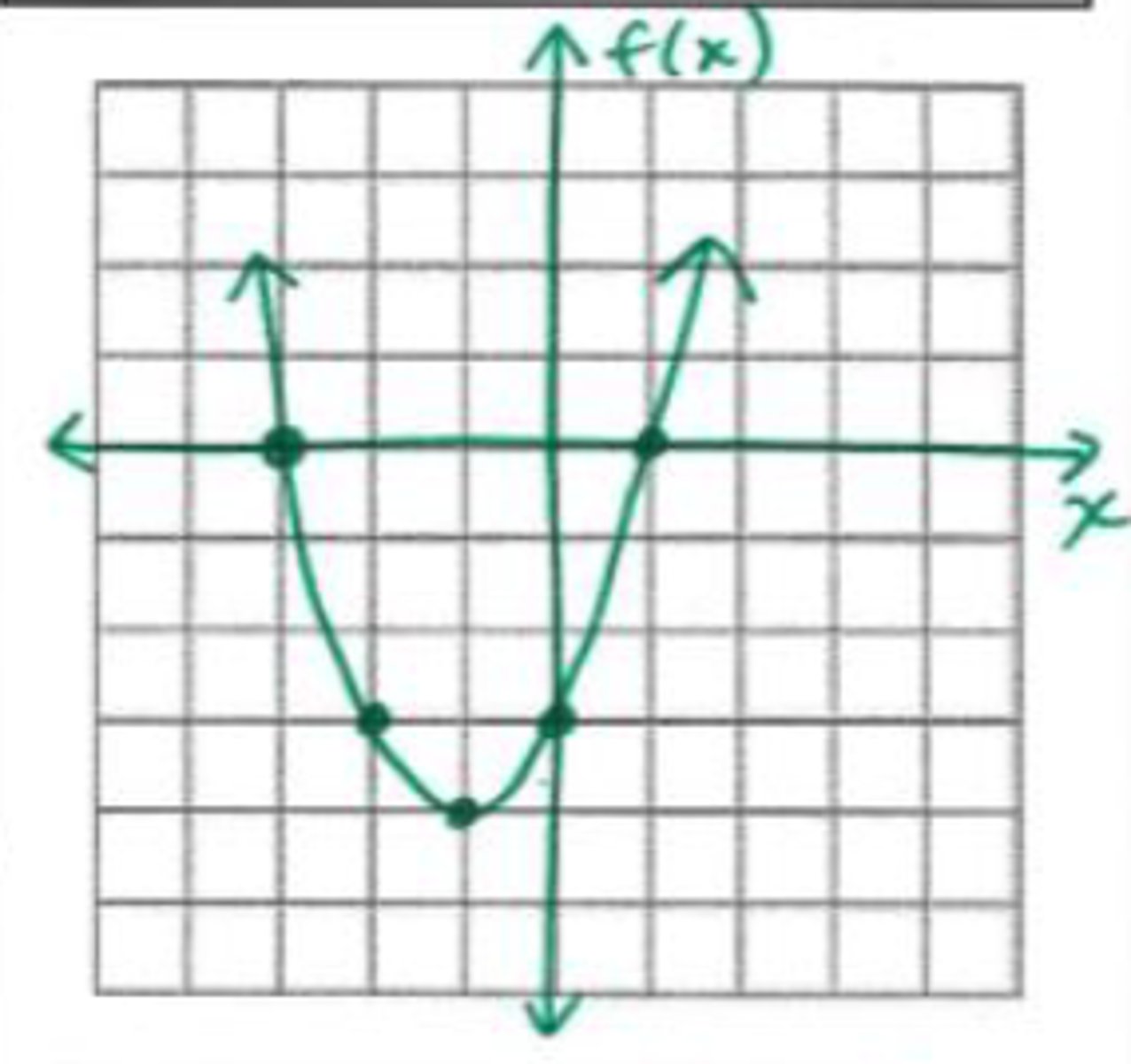
x = 0

What is the axis of symmetry in the graph shown?

(0, -4)

What is the vertex in the graph shown?

domain: all reals; range: y ≤ -4

What is the domain and range in the graph shown?

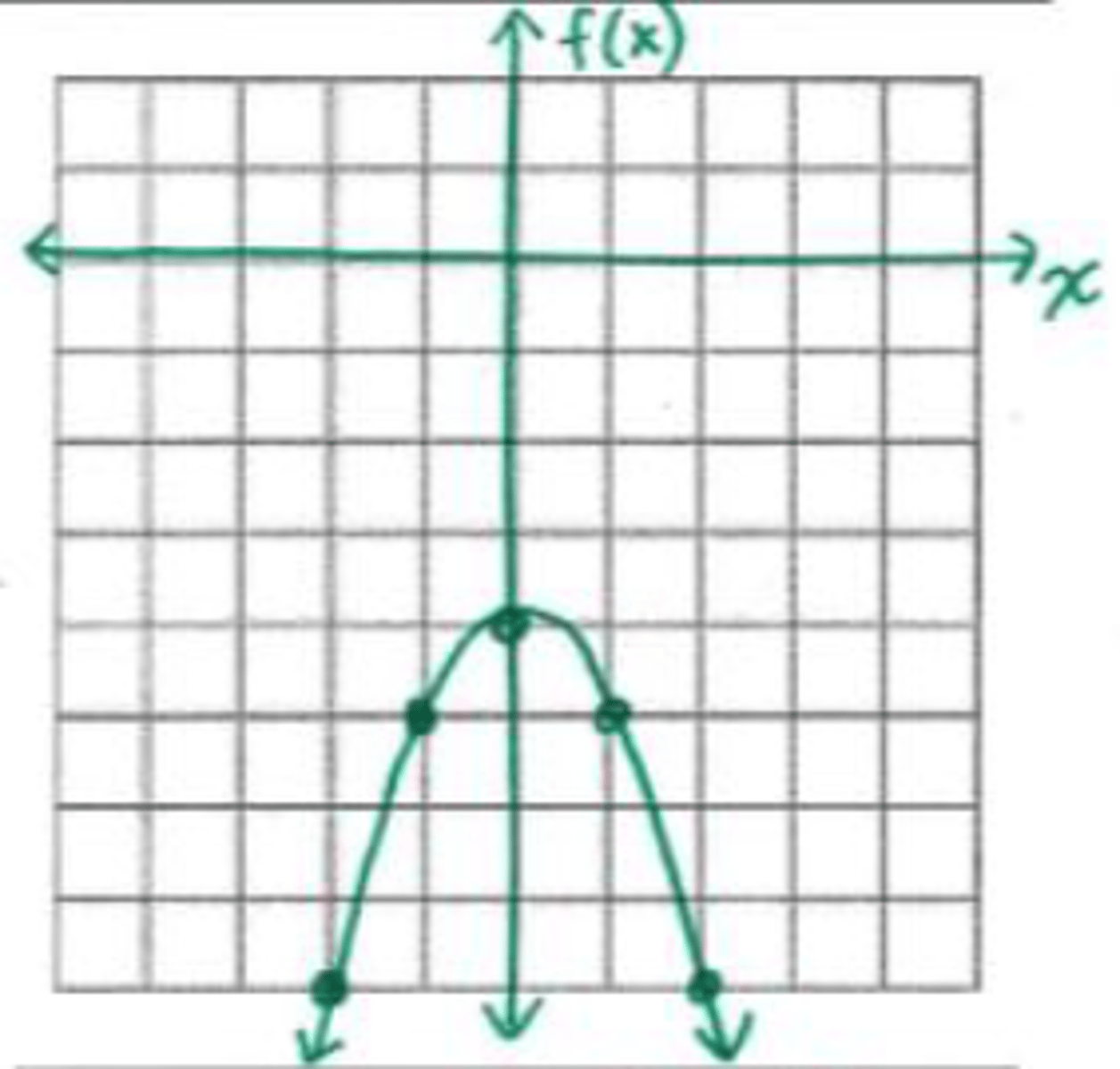
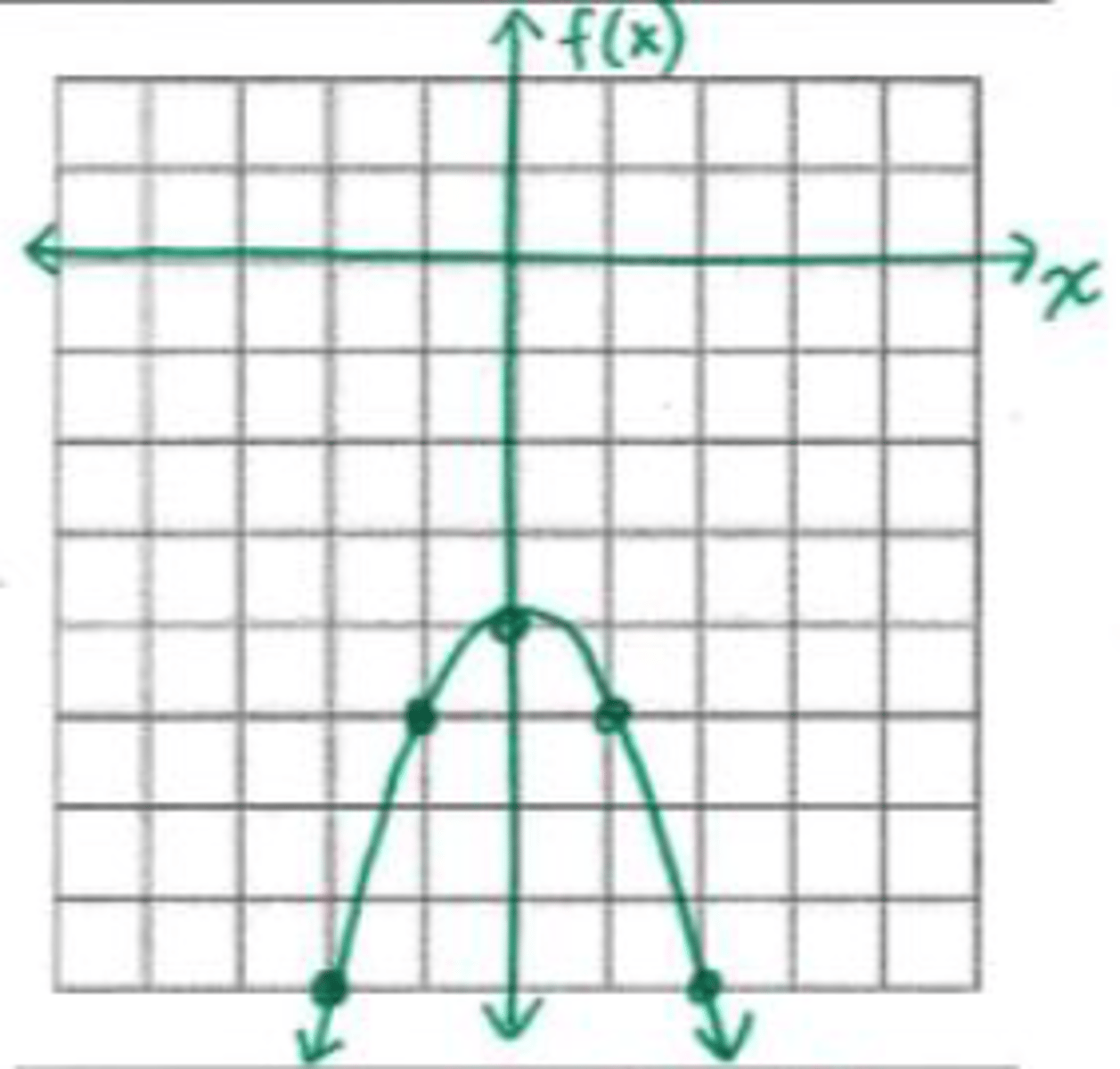
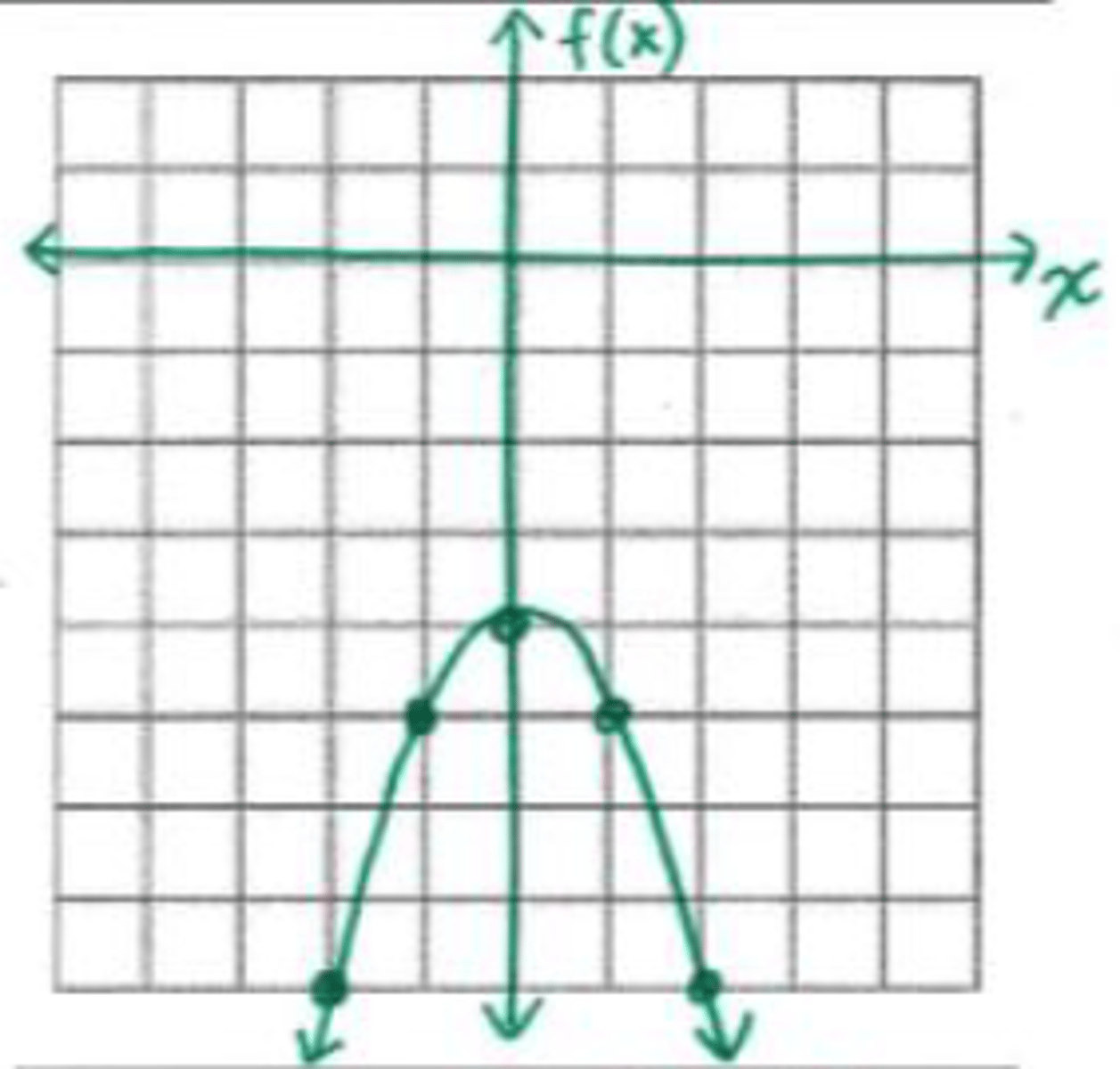
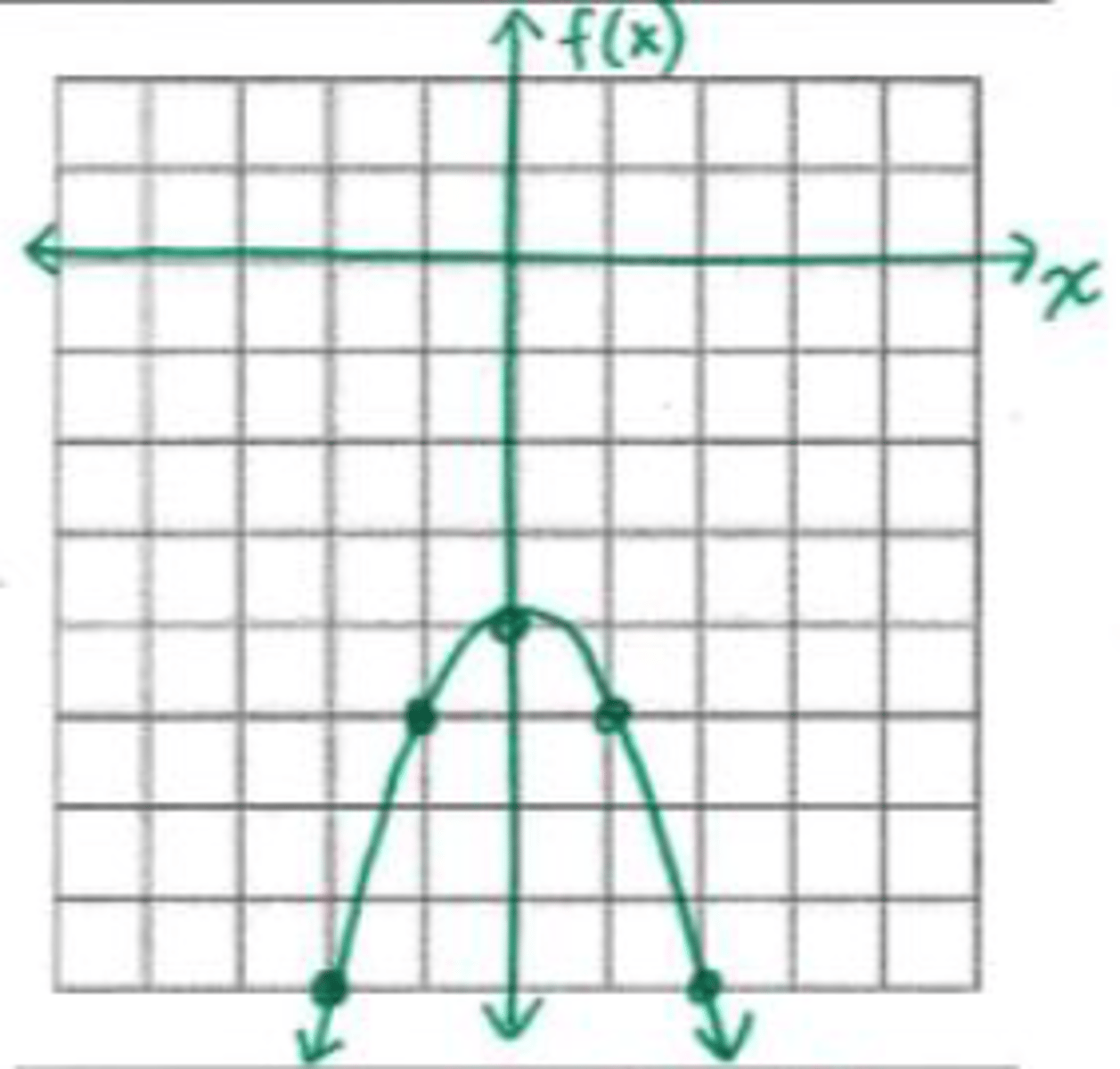
x = {∅}

What are the roots of the graph shown?

Translation of f(x)= x² up 2 units

Describe how the graph of g(x)=x²+2 is related to the graph f(x)=x²

Translation of f(x)=x² to the right one unit

Describe how the graph of g(x)=(x-1)² is related to the graph f(x)=x²

Translation of f(x)=x² down 8 units

Describe how the graph of g(x)=x²-8 is related to the graph f(x)=x²

Stretch of f(x) = x² narrower than the graph of f(x)=x²

Describe how the graph of g(x)=7x² is related to the graph f(x)=x²

Compression of f(x)=x² wider than the graph of f(x)=x²

Describe how the graph of g(x)=1/5 x² is related to the graph f(x)=x²

Stretch of f(x)=x² narrower than the graph of f(x)=x² reflected over the x-axis.

Describe how the graph of g(x)=-6x² is related to the graph f(x)=x²

Reflection of f(x)=x² over the x-axis translated up 3 units

Describe how the graph of g(x)=-x²+3 is related to the graph f(x)=x²

Compression of f(x)=x² wider than the graph of f(x)=x² reflected over the x-axis translated up 5 units.

Describe how the graph of g(x)=-½x² + 5 is related to the graph f(x)=x²

Stretch of f(x)=x² narrower than the graph of f(x)=x² translated to the right 1 unit

Describe how the graph of g(x)=4(x-1)² is related to the graph f(x)=x²

Translation of f(x)=x² to the left 10 units

Describe how the graph of g(x)=(x + 10)² is related to the graph f(x)= x²

Translation of f(x)=x² down 2/5 units

Describe how the graph of g(x) = x² - 2/5 is related to the graph f(x)=x²

Reflection of f(x)=x² across the x-axis translated up 9 units

Describe how the graph of g(x)= -x² + 9 is related to the graph f(x)=x²

Stretch of f(x) = x² narrower than the graph of f(x) translated up 2 units.

Describe how the graph of g(x)= 2x² + 2 is related to the graph f(x)=x²

Compression of f(x)=x² wider than the graph of f(x)=x², reflected over the x-axis, translated down ½ unit.

Describe how the graph of g(x)= -¾x² - ½ is related to the graph f(x)=x²

Stretch of f(x)=x² narrower than the graph of f(x)=x², reflected over the x-axis translated to the left 4 units.

Describe how the graph of g(x)=-3(x + 4)² is related to the graph f(x)=x²

{-7, 7}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: x² - 49=0

{-4, 5}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: x² - x - 20=0

{-4, 9}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: x² - 5x - 36=0

{-6, -5}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: x²+11x+30=0

{0.5, 6.5}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: x²-7x=-3

{-3.7, -0.3}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: x²+4x=-1

no real solutions

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: x²-9x+22=0

{-5.4, -0.6}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: x²+6x+3=0

{-3½, 1}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary 2x²+5x-7=0

{½, 1}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: 2x²-3x=-1

∅

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: 2x²+5x+4=0

{-4½, 1}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: 2x²+7x=9

{-1.4, 0.7}

Solve by using the Quadratic Formula. Round to the nearest tenth if necessary: 3x²+2x-3=0