Biology HL statistics

Mean

sum of the data points divided by the number of data points

Normal distribution

Bell curve.

Occurs when you have a large sample size only (as their sample means are more likely to be closer to the population mean which will cause less variation)

has a spike in the middle with the most values, and fewer on either side

Tall and narrow when values are closer together

flatter and wider if data is more spread out

mean value at the peak of the curve

x

represents a single value

n

represents the total number of values in a set

x bar. x

mean of a set of values

Σ

the sum of values

s

standard deviation of a sample

±

plus or minus

to do a t test or analyse a spread using standard deviation

requires a spread of data close to normal distribution, this is why its best to get as

Standard deviation

shows the spread of all the values around the mean. shows variability of the data set. 68% of the data lies around the 1 standard deviation from the mean on the horizontal axis

higher standard deviation, more spread around the mean

lower standard deviation, less spread around the mean, more clumped together

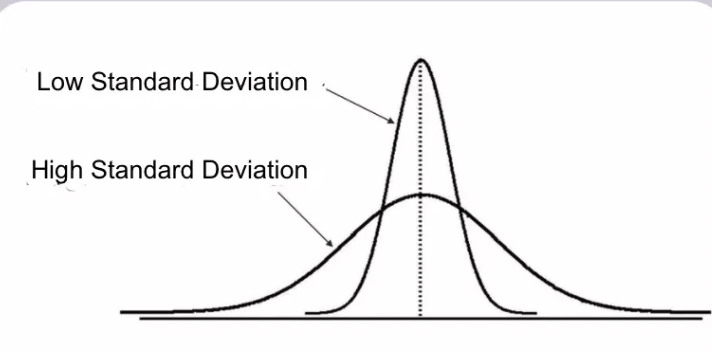
What percent of the values in a sample fall within +-1 standard deviation from the mean

68%

What percent of the values in a sample fall within +-2 standard deviation from the mean

95%

variability

Measure of how spread out the data is from the centre of the data, which can be the mean

how to calculate two standard deviations from one

multiply by two

how to calculate standard deviation

on excel type in STDEV(highlight all boxes)

higher/lower standard deviation

higher- more lower-less variation

Standard deviation can give additional information on

whether the differences between two samples are likely to be significant. The mean can be the same, but the spread around the mean can be different.

error bars

a way of showing either range or standard deviation of data, show variability

Range

spread of data from the lowest to highest value in the distribution

How do error bars work

The mean is plotted either on a bar graph or a scattered plot graph, and the error bar is plotted around the mean

to show the highest and lowest values in the set (this shows the range) (used on smaller sets).

to show standard deviation (used in bigger sets as then you have enough values for normal distribution

To find the range of values in standard deviation

add and subtract the standard deviation from the mean

t -test

Used to find if the difference between two sets of data is significant

the t test compares

mean and standard deviation of two sets of samples to see if they are the same or different (leaves on tree in front and leaves on tree in back of school)

how to calculate p value

a value for t value is calculated using a formula

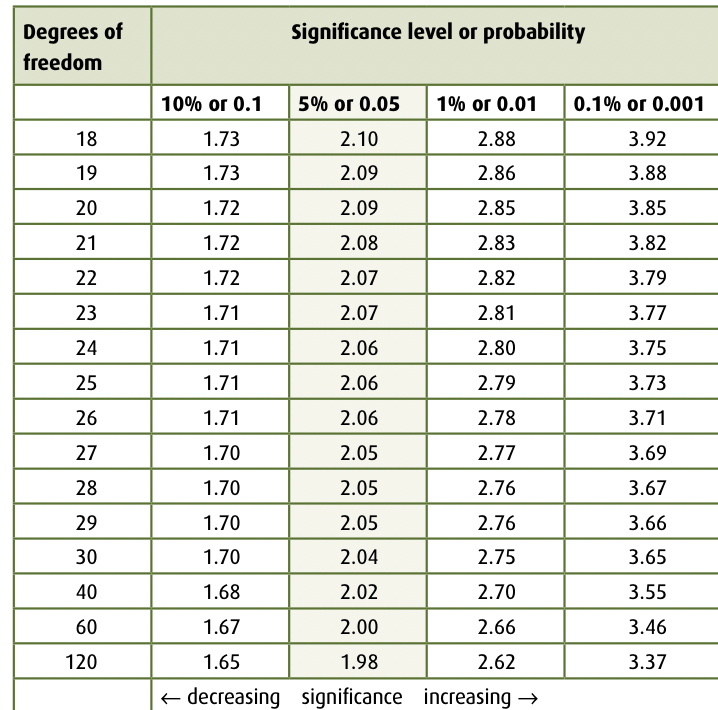
find degrees of freedom (calculated from the sum of the sample sizes of the two groups of data minus two.

degrees of freedom = (n1 + n2) − 1. number of values in sample is n

find the t value on that degrees of freedom, and then find the p value, can be a range between two percentages

You can also look at critical value for 5% and then look if your t value is greater or less than that to estimate if it would be statistically significant or not

p value

the probability that the difference between the two data sets were caused by chance

under 5% is

statistically significant as it shows that 95% or more of the time, the differences between the two data sets were not caused by chance, therefore you must deny the null hypothesis

5 % is a

critical value, scientists take this into account because living things have natural variation that can cause differences in the data sets, but at some line the differences were no longer due to this chance

Null hypothesis

there is no significant difference between the two data sets (above 5%)

Alternative hypothesis

there is a significant difference between the two data sets (below 5%)

What if you get a value like 6-15%

conclusion is less certain. if you suspect null hypothesis still, that there is no significant difference, make a bigger sample size

population vs sample set

All the students in the class vs the top ten students

Correlation

describes the degree of a relationship between two variables

what can correlation do

de establish a casual relationship between 2 variables

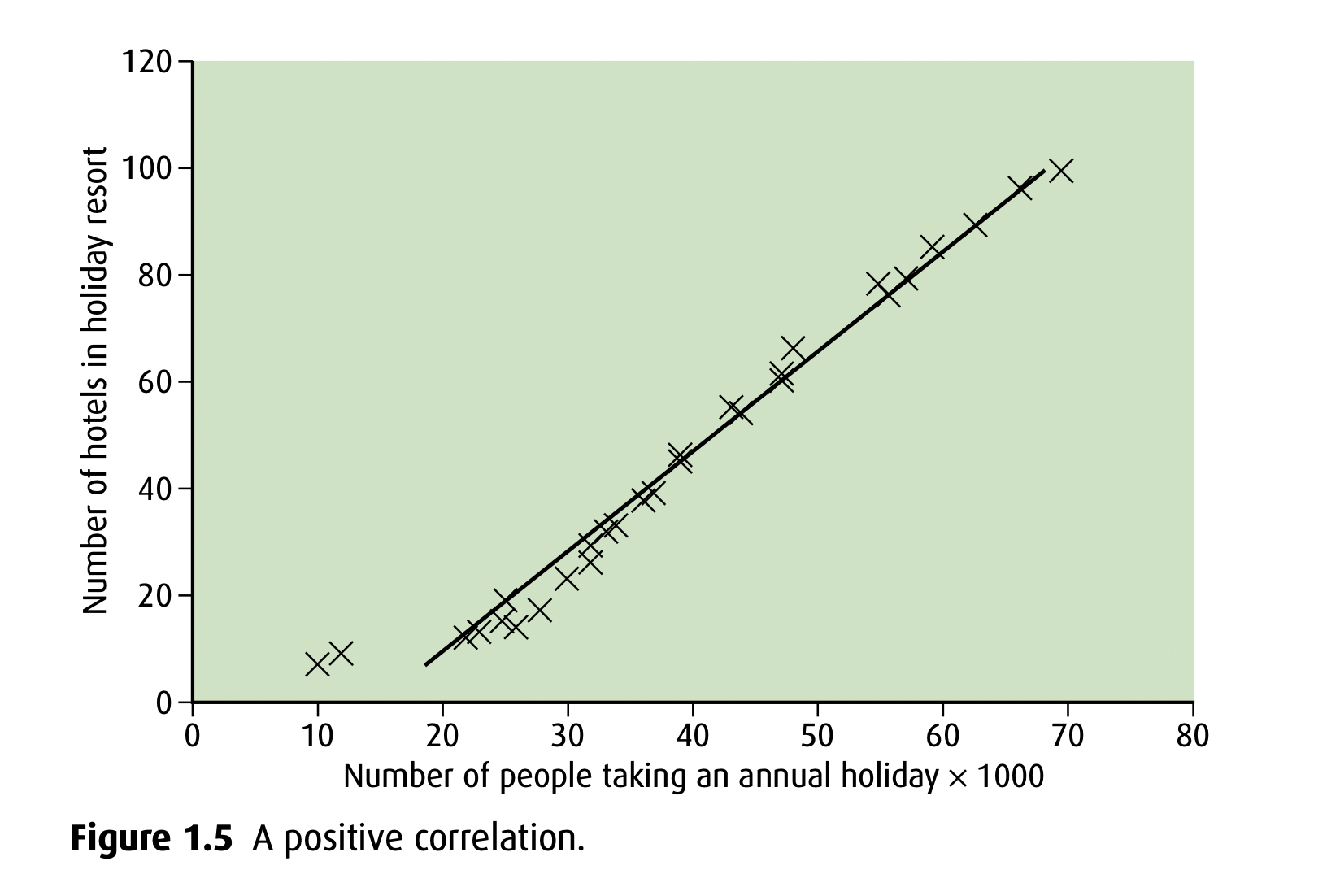
Positive correlation

as x value increases, so does y value

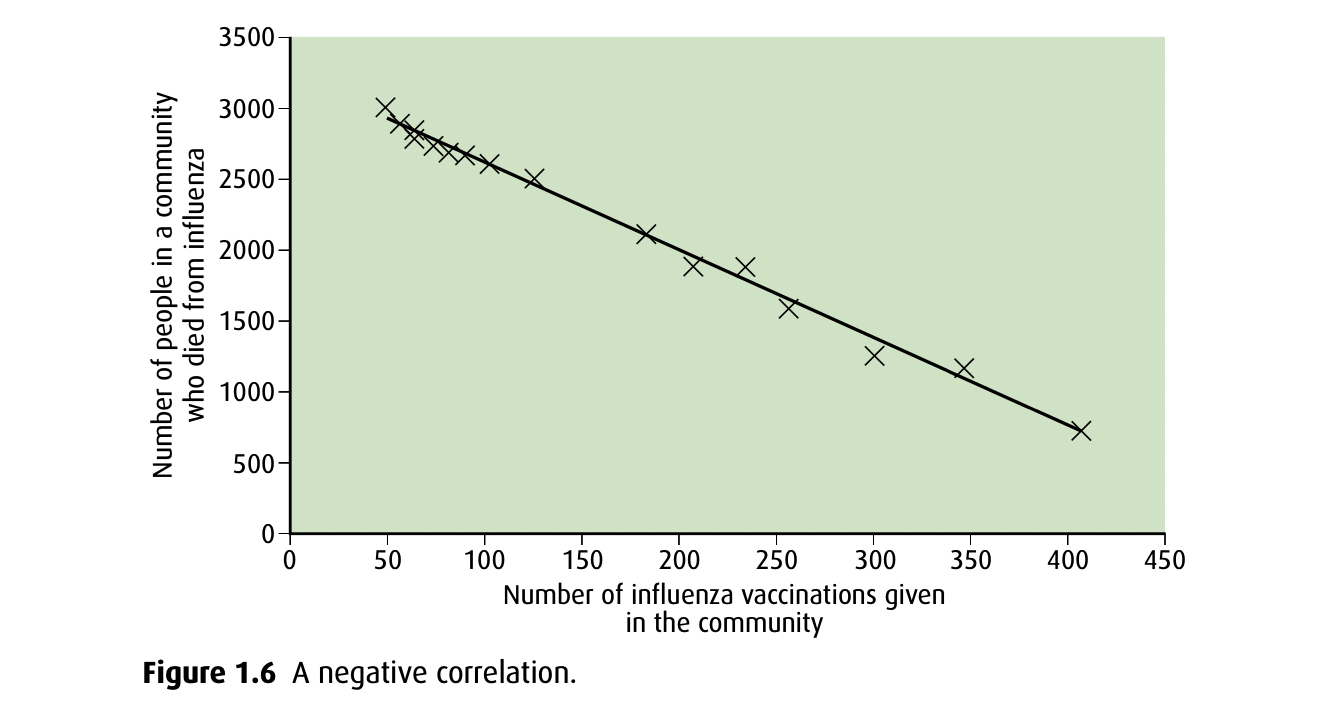
Negative correlation

as x value increases, y value decreases, inversely proportional relationship

Casual relationship

If the occurrence of one variable causes the other (more vaccines, less deaths, negative correlation)

Does a trend always mean a Casal relationship

No, the two variables can be totally unrelated and still show a trend. Experiments must be used to provide evidence showing the cause of the correlation

Median

Middle value of a range of results. Useful if you have outliers

Mode

value that appears the greatest number of times

Continuous variation

Quantitative

Different characteristics within a population

Range

Height, body mass, intelligence

Discontinuous

Either have it or you dont

distinct features

qualititative

Tongue roll, ear lobe, blood group

Positively skewed

tail on the positive end

negatively skewed

tail on the negative end

Error analysis

evaluating the uncertainty associated with a data measurement

Double blinded

Doctor and patients do not know who has placebo or real thing

Interquartile range

calculate main median, and then split up the two groups and calculate their medians, then subtract the 25% median from 75% median to find IQR. shows the range of the middle 50% of your sample. useful with outliers

standard error

Calculates how representative your sample is of your population, how accurate a random sample’s mean would be in comparison with the population’s mean

Calculated using SD and sample size

You can decrease this by having a larger sample size

Standard error vs. standard deviation

Standard deviation is variability within a sample standard error is variability across samples

High Standard error vs low standard error

High- data is widely spread around population

Low- Data is closely distributed around population

Higher mean on graph

Bell curve shifts to the right

Higher frequency of the mean on graph

Bell curve becomes taller and thinner

Pearson correlation coefficient r and R²

Used when data is continuous and normally distributed

Measures the strength and direction of the two variables

(+1- perfect positive correlation, 0- no correlation, -1 perfect negative correlation), the strength of a linear relationship between two variables

r² shows variability in the data, measure of how well the data fits the linear model, how far the points are from the line

•0% represents a model that does not explain any of the variance in the data

•100% represents a model that explains all of the variance in the data

aim for 80% or higher

Spearman test

Can be used with discontinuous data as well as continuous

same as the “r s” explained above, explains the strength and direction of the relationship of the two variables

error bars overlap

share the same values

Variation

A general description of the difference between any two measurements

how to know if the difference in the two sets of data in a t test are caused by the independent variable

Because they will be higher than the t value for the critical p value 5%, showing that they are lower than 5% and the differences are most likely not caused to chance

as p value decreases

t value increases