Math 10 - Lecture 5

Shapes

Geometry

Derived from Greek words geo (earth) and metron (measurement); developed to deal with measuring areas, lengths, and volumes in early civilizations.

Plato’s Geometry Quote

Let no one enter, who is ignorant of Geometry

Origins of Geometry

1. Before Euclid

2. Euclidean Geometry

3. Non-Euclidean Geometry

4. Projective Geometry

5. Topology

Before Euclid

• The period of geometry before the discoveries of Euclid of Alexandria

• Includes the geometry concepts in Babylon, Egypt, and Greece

Babylonian Mathematics

Found in ~400 clay tablets written in cuneiform script; included formulas for finding areas and volumes, particularly of circles and cylinders.

Babylonian Approximation of π (Pi)

Value of 3, considering the circumference to be three times the diameter.

Babylonian Approximation of Circle Area

One-twelfth of the square of the circumference.

Babylonian Knowledge of Pythagorean Theorem

Had records suggesting early cases of the Pythagorean Theorem, known currently to us as the Pythagorean Triples.

Modern Use of Babylonian Geometry

Their methods influenced foundational practices in calculating areas, volumes, and early architectural design, especially regarding circles.

Egyptian Mathematics

Developed alongside Babylonians; created formulas for areas and volumes essential for pyramid construction and managing food resources.

Ahmes Papyrus

A significant Egyptian document (circa 1650 BC) containing arithmetic, algebraic, and geometric problems; key source for understanding Egyptian mathematics.

Rhind Mathematical Papyrus

Alternate name of Ahmes Papyrus

First Part of the Ahmes Papyrus

Covers around 21 arithmetic and 20 algebraic problems.

Second Part of the Ahmes Papyrus

Covers problems 41-59, 59B, and 60 that are geometry problems.

Egyptian Middle Kingdom

The place where the Rhind papyrus was found from.

Henry Rhind

The man who purchased the Ahmes Papyrus in Egypt in 1858.

Eratosthenes

Greek mathematician who first calculated the Earth’s circumference with high accuracy using geometric methods.

Pythagoras

Introduced the relationship a²+b²=c² in right triangles, a foundational principle in geometry.

Pythagorean Theorem

The theorem in which the hypotenuse of a right triangle could be calculated using its base and length.

Archimedes of Syracuse

Greek mathematician known for discovering methods to calculate the areas and volumes of irregular shapes and for accurately approximating π.

Method of Exhaustion

An early form of integration developed by Eudoxus of Cnidus and used by Archimedes to find areas and volumes.

Greek Discovery of Irrational Numbers

Identified numbers like √2 and π that cannot be expressed as ratios of integers.

Golden Ratio (φ)

A special ratio (~0.618) where dividing a line such that the whole is to the longer part as the longer is to the shorter produces the golden ratio.

Golden Ratio Equation

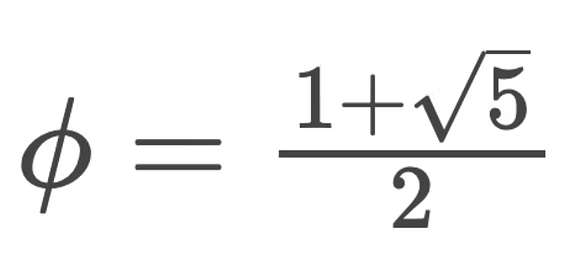
Golden Rectangles

Rectangles where the ratio of length to width is φ (golden ratio); considered the most aesthetically pleasing proportions.

Reciprocal of the Golden Ratio

1.618

Euclid

• Greek mathematician, known as the “Father of Geometry”.

• Author of The Elements, a 13-book compilation of mathematical knowledge.

The Elements (Euclid)

• A comprehensive work in 13 books organizing geometry and number theory.

• Remained a central textbook for over 2000 years.

Euclidean Geometry

• Geometry based on Euclid’s postulates and common notions

• Includes plane and solid geometry in flat space.

Axioms

• Common notions.

• Basic assumptions considered universally true, such as "Things equal to the same thing are equal to each other."

Euclid’s Axioms

1. Things that are equal to the same thing are equal.

2. If equals are added to equals, then the whole are equal.

3. If equals are subtracted from equal, then the remainders are equal.

4. Things that coincide with one another are equal to one another.

5. The whole is greater than the part.

Euclidean Triangles

• Axiomatic system on triangles based on congruency and similarity.

• Always have a total sum of their interior angles to be 180 degrees.

Congruence

• Two figures are congruent if they have the same shape and size; important in proving geometric theorems.

• Same size meaning:

  • Sides are of the same lengths

  • Angles are equal

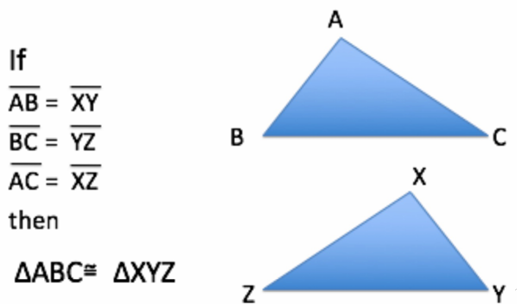
SSS Congruence

• Three corresponding sides are congruent.

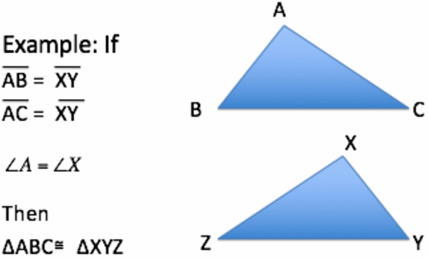
SAS Congruence

• Two corresponding sides and the angle between them are congruent.

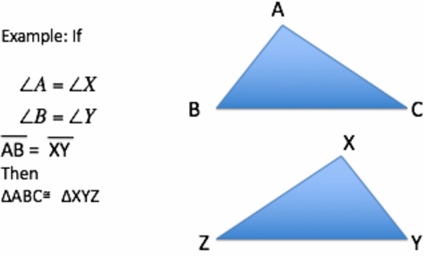
ASA Congruence

• Two corresponding angles and the side they include are congruent.

Similarity

• When two shapes have the same general shape but can be different sizes.

• Their three corresponding angles are equal.

Postulates

• Geometric assumptions accepted without proof.

• Specific to geometry; the foundation of Euclidean constructions.

Euclid’s Five Postulates

1. A straight line can be drawn from any point to any point.

2. A finite straight line can be extended continuously in a straight line.

3. A circle can be drawn with any center and radius.

4. All right angles are equal.

5. If a line intersects two others and the interior angles sum to less than two right angles, they meet on that side.

Parallel Postulate

• The fifth postulate; more complex than the others

• Led to centuries of debate and eventually to non-Euclidean geometries.

Postulate 1

A straight line can be drawn from any point to any point.

Postulate 2

A finite straight line can be produced continuously in a straight line.

Postulate 3

A circle may be drawn with any point as center and any distance as radius.

Postulate 4

All right angles are equal to one another.

Point (Euclid's Definition)

• That which has no part

• An exact position or location in space.

Line (Euclid's Definition)

• Breadthless length

• Having only one dimension — length.

Surface (Euclid’s Definition)

• That which has length and breadth only (two dimensions).

Angle

• Formed by two lines originating from the same point

• Includes right, acute, and obtuse angles.

Right Angle

• Formed when a straight line standing on another makes adjacent angles equal.

Perpendicular Lines

• Two lines that form right angles with each other.

Acute Triangle

• A triangle with all angles being less than 90^o.

Right Triangle

• A triangle with one angle being exactly 90^o.

Obtuse Triangle

• A triangle with one angle being more than 90^o.

Equilateral Triangle

• A triangle with all sides being equal length.

Isosceles Triangle

• A triangle with only two sides being equal length.

Scalene Triangle

• A triangle that has no equal sides.

Non-Euclidean Geometry

• A type of geometry that modifies or rejects Euclid’s fifth postulate (parallel postulate).

• Led to new geometrical systems.

Why Non-Euclidean Geometry Emerged

• Mathematicians sought to prove Euclid’s fifth postulate from the others but failed.

• Instead, modifying it created consistent alternative geometries.

Nikolai Ivanovich Lobachevsky

• Russian mathematician and geometer

• Published works formalizing hyperbolic geometry, independently of Gauss and Bolyai, in 1829.

Geometrische Untersuchungen zur Theorie der Parellellinien

• A work by Lobachevsky published in 1829.

Janos Bolyai

• Hungarian mathematician

• Independently developed hyperbolic geometry, published it as an appendix to his father’s book in 1832.

Johann Carl Friedrich Gauss

• German mathematician

• Privately developed non-Euclidean ideas but didn’t publish due to fear of controversy

• Considered one of the first to realize its consistency.

Hyperbolic Geometry

• A geometry where through a point not on a line, more than one line can be drawn parallel to the given line.

• Space is curved negatively like a saddle.

Hyperbolic Geometry Postulate

Through a point P not on a line L, there exists at least two lines passing through point P parallel to line L.

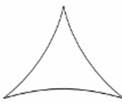
Hyperbolic Triangle

• A triangle with the sum of its internal angles being less than 180 degrees.

• Similar triangles of these types are also congruent.

Elliptic Geometry

• A geometry where no parallel lines exist

• Space is curved positively, like the surface of a sphere.

Lines and Points in Elliptical Geometry

• Points are on the surface of the globe.

• Lines are the great circles, which are circles of maximum diameter on the surface of the globe.

Elliptical Geometry Postulate

Through a point P not on a line L there exists no line passing through point P parallel to line L.

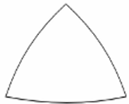
Elliptical Triangle

• A triangle with the sum of its internal angles being more than 180 degrees.

• Similar triangles of these types are also congruent.

Parallel Lines in Euclidean Geometry

• One truly unique parallel line.

Parallel Lines in Hyperbolic Geometry

• Infinitely many parallel lines.

Parallel Lines in Elliptical Geometry

• No parallel lines exist.

George Friedrich Bernhard Riemann

• German mathematician.

• Developed elliptic geometry, also named after his own last name.

Projective Geometry

• A branch of geometry studying properties invariant under projection.

• Ignores measurements like distance and angle.

Key Principle of Projective Geometry

• Focuses on how figures relate through projection, and not measurement.

• Parallel lines intersect at a point at infinity.

Gerard Desargues

• French mathematician and engineer who founded projective geometry.

• Revisited Euclid’s 2nd postulate and is then known for a theorem on triangles in perspective.

Desargues’ Theorem

• States that if two triangles are in perspective from a point, they are in perspective from a line (and vice versa).

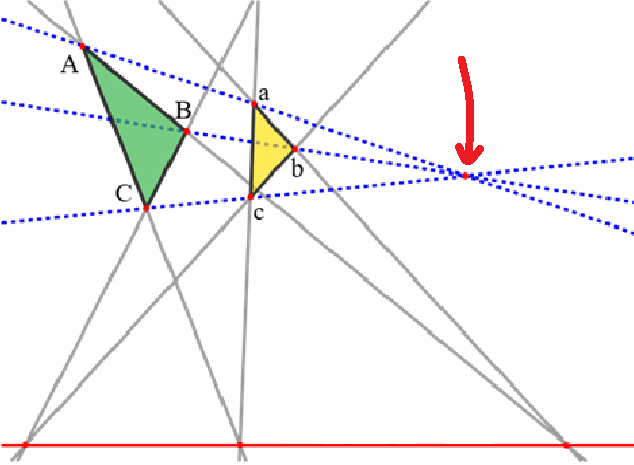
Center of Perspectivity

• The point where lines drawn from corresponding vertices of two perspective figures meet.

• In triangle perspective, it is where lines connecting corresponding points intersect.

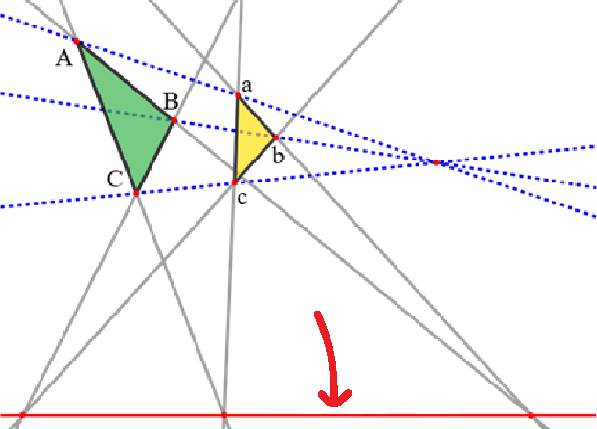
Axis of Perspectivity

• The line on which the intersections of corresponding sides of two perspective triangles lie.

• If triangles are in perspective from a point, their sides intersect in collinear points on this axis.

Three-Dimensional Perspective

A technique for representing 3D objects on a 2D surface by projecting points through a center of perspective (eye or camera) onto a plane, preserving the appearance of depth and relative position.

Topology

Study of properties that remain unchanged under continuous deformation (stretching, bending, but not tearing or gluing).

17th Century Understanding

• Space was conceptualized as a set of points together with an abstract set of relations in which these points are involved.

• Geometry = Theory of Space of Points

Origin of Topology

• Emerged from geometry and set theory in the 19th century

• Rooted in the study of shapes’ intrinsic properties.

Jules-Henri Poincare

• Published a book titled Vorstudien zur Topologie that described the concept of topology.

• First to publish a book in 1895, but topology was not a novel concept.

Topological Transformations

• Any transformation like stretching, shrinking, twisting, or bending that allows the points to remain distinct.

• Does not include cutting, tearing, puncturing, and merging points.

Topological Properties

• Properties unchanged by continuous deformation, such as connectedness, compactness, and genus.

Genus (Topology)

• A measure of the number of holes in a surface; e.g., a sphere has genus 0, a torus has genus 1.

Mobius Strip

• A surface with only one side and one boundary; created by twisting a strip and connecting the ends.

Riemannian Geometry

• A non-Euclidean geometry concept developed by Bernhard Riemann.

• Also called Elliptic Geometry

• Provided the framework for Einstein’s Theory of General Relativity.