chapter 8 gases part 2

kinetic theory of gases postulates

gas particle volume is zero, gas particles are in constant random directional motion in straight lines, change direction when colliding with other molecules or container walls, obey newton’s laws, elastic particle collisions

what conversion factor should i always remember

g to kg(SI)

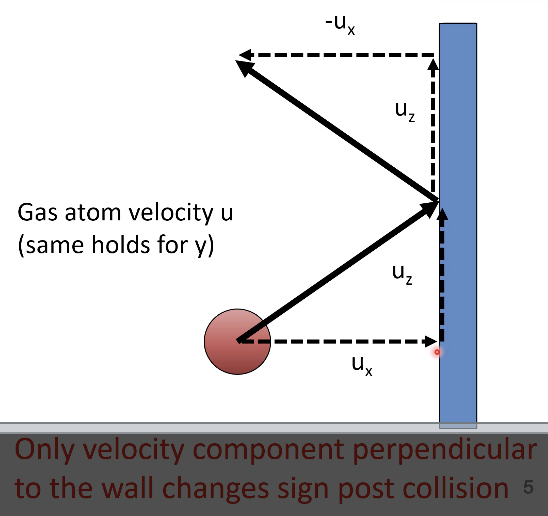
when gas atom collides with wall

only velocity component perpendicular to the wall changes sign

P =

1/3 * N/V * m * mean(u²) where N is number of particles, m is mass of a particle, and mean square velocity

PV =

2/3 * avg kinetic energy (1/2 m u² avg) = 1/3 * N m u²avg

T =

1/3 * N_A/R * m u²avg, shows that temperature depends on velocity

average KE of a gas molecule

3/2 RT/N_A

with root mean square velocity we can see that

as temperature increases, so does rms

as molar mass increases, rms decreases

root mean square velocity =

√3RT/M

effusion

process by which a gas escapes through a tiny hole into a vacuum

law of effusion and diffusion

Rate_A/Rate_B = √M_B/M_A

diffusion

random movement of one gas through another e.g. drop of ink into water

mean free path

average distance a gas molecule travels between collision

collision frequency

the average number of collisions per second per gas molecule

real/non-ideal gases

gas molecules are not compressible, results in higher pressures than under ideal gas law - excluded volume starts playing a role

real gas molecules will

attract each other at short distances

van der waals equation

(P + n²/V² a)(V - nb) = nRT, where first term accounts for intermolecular attraction and second accounts for excluded volume. a and b are vdw constants

ideal gas behaviour observed at

high temperatures and low pressures

non-ideal gas behaviour observed at

low temperatures and high pressures

compressibility factor

Z = PV/nRT

if z = 1, >1, or <1

ideal gas, excluded volume dominates, attractive forces dominate