Quantum mechanics I

Difference b/w Classical and Quantum Mechanics

👉 Classical Mechanics

1. Macroparticles – Ye bade objects ke liye use hota hai (jaise car, planets, ball, etc).

2. Certainty – Yahan sab kuch exact predict kiya ja sakta hai. Agar aapko initial position aur velocity pata ho toh future motion predict kar sakte ho.

3. Continuous – Energy ya motion continuous mana jata hai (koi breaks nahi).

👉 Quantum Mechanics

1. Microparticles – Ye chhoti cheezon ke liye apply hota hai (jaise electrons, protons, atoms).

2. Uncertainty – Yahan exact position aur momentum ek sath predict karna possible nahi (Heisenberg’s Uncertainty Principle).

3. Discontinuous – Energy discrete hoti hai, packets (quanta/photons) ke form mein.

Blackbody kya hota hai?

Blackbody = ek aisi ideal body jo apne upar girne wali sari radiation (light, heat, etc.) ko absorb kar leti hai.

Matlab wo kuch reflect nahi karti, kuch transmit nahi karti, sirf absorb karti hai.

Baad mein wo absorbed energy ko apne temperature ke hisaab se emit karti hai.

👉 Is emitted radiation ko hi blackbody radiation bolte hain.

📌 Example socho: ek perfect black box jisme chhota sa hole ho → jo bhi light andar jayegi, wo phas jaayegi aur absorb ho jayegi. Bahar aane ka chance almost zero hai. Ye ek ideal blackbody ka model maana jata hai.

Experiment by Lummer & Pringsheim

Ye dono German scientists the (1890s ke around).

Unhone blackbody radiation ko measure karne ke liye ek accurate setup banaya.

Ek hollow cavity blackbody banayi jisme chhota hole tha. Is hole se jo radiation bahar aati thi usko study kiya.

Phir unhone intensity of radiation vs wavelength ke graphs (curves) nikale different temperatures par.

👉 Result kya mila?

1. Har temperature par ek specific wavelength pe radiation ka maximum hota hai.

2. Jaise-jaise temperature badhta hai, maximum wali wavelength chhoti hoti jati hai (yaani hotter body → shorter wavelength → zyada bluish light).

Yahi baad mein Planck, Wien aur Rayleigh-Jeans laws ko samjhane ke liye foundation bana.

---

⚡ Easy Formula yaad rakhne ke liye (jo Lummer–Pringsheim curves se mila):

Higher T → peak shift towards shorter λ

(Example: garam loha lal chamakta hai, aur aur zyada heat karne pe sa

fed/bluish chamakta hai).

Graph Explanation (Lummer & Pringsheim)

Graph ka axis:

Vertical (Y-axis) → Energy radiated (Eλ)

Horizontal (X-axis) → Wavelength (λ)

Curves: T₃ > T₂ > T₁ (yaani T₃ sabse zyada temperature hai, T₁ sabse kam).

---

🔑 Characteristics of the Curves

1. For each temperature → ek specific wavelength hoti hai jahan radiation maximum hota hai.

Matlab har curve ka ek peak point hota hai (maximum energy).

Isko λmax (wavelength of maximum emission) bolte hain.

2. Position of maxima (peak) shift karta hai:

Agar temperature decrease hota hai → maxima longer wavelength pe shift karta hai.

Agar temperature increase hota hai → maxima shorter wavelength pe shift karta hai.

👉 Ye directly Wien’s Displacement Law ko support karta hai:

λ_{\text{max}} \times T = \text{constant}

3. Higher temperature → curve ke peaks zyada pronounced aur broad hote hain.

Matlab zyada temperature pe energy distribution zyada uniform hoti hai across wavelengths.

Lower temperature pe curve narrow hota hai, energy concentration ek chhote wavelength range me hoti hai.

---

🔥 Real-Life Example:

Jab lohe ka tukda garam karte ho:

• Pehle red chamakta hai (longer wavelength, lower T).

• Fir zyada garam karoge toh orange → yellow → white → bluish chamkega (shorter wavelength, higher T).

• Yehi curve shift ka real example hai.

---

👉 Easy Hack to Remember:

T ↑ → λmax ↓ (temperature badhe toh wavelength chhoti hoti hai).

Hotter objects look bluer, colder objects look redder.

⚡Failure of Classical Theory on Blackbody Radiation

Classical physicists ne Blackbody Radiation ko explain karne ke liye alag–alag formulas diye. Do main attempts the:

---

1. Wien’s Law

Wien ne ek expression derive kiya thermodynamic considerations se.

Uska formula tha:

E_\lambda d\lambda = A_1 \lambda^{-5} e^{-A_2/\lambda T} d\lambda

jahan A₁ aur A₂ constants hain.

👉 Kya mila?

Ye formula shorter wavelength (lower λ) region mein achhe se kaam karta tha.

Lekin longer wavelength region mein ye poora fail ho gaya.

---

2. Rayleigh–Jeans Law

Rayleigh aur Jeans ne energy distribution ke liye equipartition of energy principle apply kiya.

Unhone blackbody ke radiation ka ek formula nikala:

E_\lambda d\lambda = \frac{8 \pi k T}{\lambda^4} d\lambda

👉 Kya mila?

Ye expression longer wavelength region ke liye sahi aaya.

Lekin shorter wavelength region mein ye fail ho gaya.

---

⚠ Problem:

Shorter wavelength region (UV region) mein Rayleigh–Jeans formula kehta tha ki energy infinite ho jayegi.

Isko bola jata hai “Ultraviolet Catastrophe” 🚨

---

🔑 Conclusion (Notes ka main point):

Classical expressions partial solutions dete the (koi sirf long λ pe sahi, koi sirf short λ pe sahi).

Lekin ek bhi formula pura spectrum (all wavelengths) explain nahi kar paaya.

Isi wajah se kaha gaya:

“Blackbody radiation cannot be explained by classical methods.”

Aur yahin se Quantum Mechanics ka janm hua, jab Planck ne energy quantization ka concept diya.

---

👉 Easy Memory Trick:

• Wien → Short λ (works for small range, fail for long).

• Rayleigh–Jeans → Long λ (works for long, fail for short → infinite energy problem)

Planck’s Quantum Theory (1900)

Ye theory ne classical physics ki failings ko solve kiya, specially black body radiation ka problem jisko classical laws explain nahi kar pa rahe the.

---

Main Postulates of Planck’s Quantum Theory

1. Energy ka emission/absorption continuous nahi hota, balki discrete packets (bundles) ke form mai hota hai.

• Ye discrete packets ko quanta kehte hain.

• Light ke case mai ise hum photon bolte hain.

(ii) – Energy of a Quantum

Planck ne bola ki ek radiation ke ek bundle (quantum) ki energy directly uski frequency (ν) pe depend karti hai.

Formula:

E = h\nu

E = ek quantum (photon) ki energy

h = Planck’s constant (6.626 × 10⁻³⁴ Js)

= frequency of radiation

---

🔑 Matlab kya hua?

Agar frequency zyada hai → har quantum ki energy bhi zyada hogi.

Agar frequency kam hai → energy bhi kam hogi.

Yaani light ka rang (frequency) decide karta hai ki ek photon kitni “powerful” hai.

---

🔥 Example:

Red light (ν kam) → photon ki energy kam hoti hai.

Blue/UV light (ν high) → photon ki energy bahut zyada hoti hai.

Isiliye UV rays skin ko damage kar dete hain, par red light harmless hoti hai.

3.Body energy ko sirf poore quanta ke multiples mai absorb/emit kar sakti hai.

• Matlab energy levels quantized hain:

• E_n = nh\nu, \quad n = 0, 1, 2, 3, …

4. Ye quantization ka idea hi black body radiation ka spectrum sahi se explain karta hai.

Short wavelength region (high frequency) aur long wavelength region dono match kar gaye Planck ke equation se.

---

👉 Simple analogy socho:

Classical physics kehti thi ke energy ek smooth river ki tarah hai — har level pe flow karegi.

Planck ne bola: “No bhai, ye toh coins ki tarah hai — sirf poore coins (discrete packets) hi diye jaa sakte hain, change (fractions) nahi milega!”

Isi wajah se quantum mechanics ki

foundation rakhi gayi. 🚀

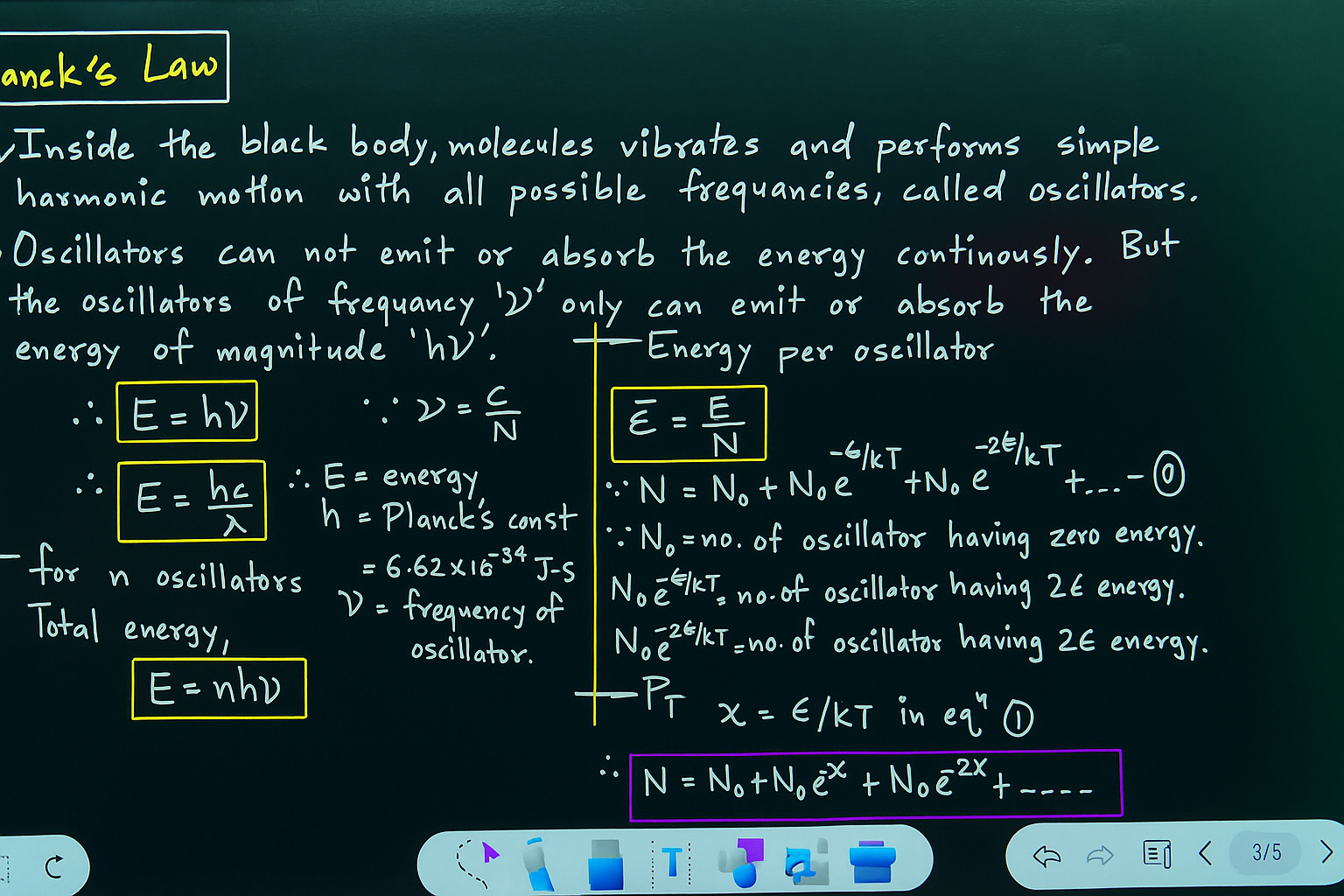
Planck radiation formula

Wiens law using planck radiation law

de broglie

Davissson- German exp

🔹 Background

De Broglie ne bola tha ki electrons ka dual nature hota hai → particle bhi hai aur wave bhi.

Agar electron wave hai, toh uska diffraction (tirchha bikharna) aur interference possible hona chahiye (jaise X-rays crystals se diffract hote hain).

Is baat ko experimentally prove kiya Davisson aur Germer ne 1927 mai.

---

🔹 Experiment Setup

1. Electron source:

Ek heated filament se electrons nikale.

Unko ek potential difference (40V–68V) se accelerate kiya → iska matlab unhe energy mili.

2. Collimator:

Yeh ek slit hota hai jo electron beam ko straight aur narrow banata hai.

3. Nickel Crystal Plate:

Electron beam ko nickel plate pe focus kiya gaya.

Nickel crystal ke atoms ke layers ek tarah ke "diffraction grating" banate hain.

4. Detector (Movable Collector + Galvanometer):

Nickel plate se jo electrons reflect hote hain, unko alag–alag angles pe measure kiya detector se.

Detector current (galvanometer) ke through electrons ke number ko record karta tha.

---

🔹 Observation

Electrons jab nickel plate se takraaye, toh simple reflection ke alawa unhone diffraction pattern dikhaya.

Matlab kuch specific angles pe zyada intensity mili (jaise constructive interference hota hai).

Particularly, 54 V accelerating potential pe aur 50° angle pe maximum intensity mili.

---

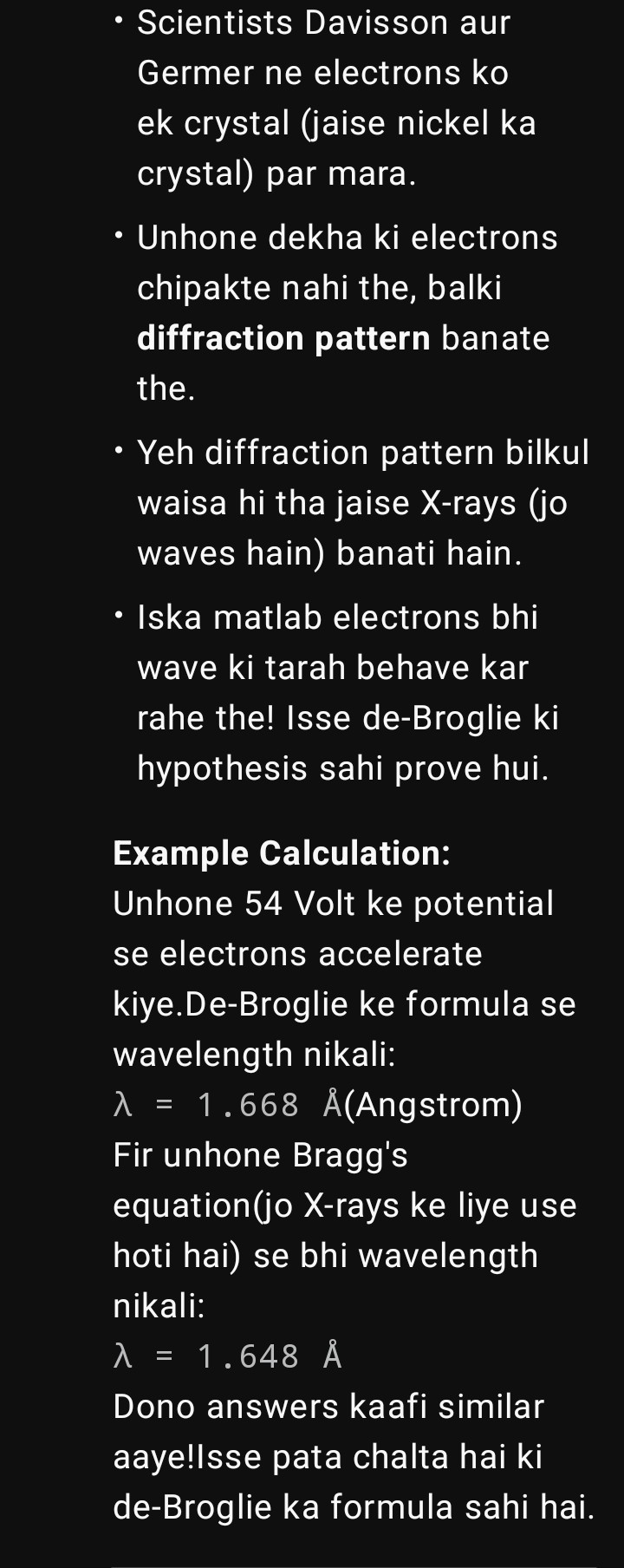
🔹 Explanation with De Broglie + Bragg’s Law

De Broglie ke hisaab se electron ka wavelength:

\lambda = \frac{h}{mv}

Experiment ke hisaab se jo λ nikla (≈1.65 Å) woh same tha jo Bragg’s diffraction law se aata hai for nickel crystal planes:

2d \sin \theta = n\lambda

Yani electron truly wave behave kar raha tha, jaise X-rays karte hain.

🔹 Conclusion

✔ Experiment ne de Broglie hypothesis ko prove kar diya → electron waves bhi hote hain.

✔ Yahi se Wave–Particle Duality solid ho gaya.

✔ Isi wajah se Electron diffraction ek accepted fact hai.

---

🔹 Bonus Info

Davisson aur G.P. Thomson ne 1937 ka Nobel Prize share kiya electron diffraction discover karne ke liye.

Interestingly, J.J. Thomson (G.P. Thomson ke father) ko pehle hi electron discovery ke liye Nobel mila tha! Matlab father ne electron ko "particle" dikhaya aur beta ne "wave" dikhaya 😄.

Solution of SWE in 1D box

"Solution of S.W.E for 1-D box"

→ Yani ek 1-Dimensional box ke liye Schrödinger Wave Equation ka solution.

---

(1) Normalised wave function

→ Yani aisi wave function jiska total probability = 1 ho.

(2) Energy

→ Iska matlab particle ki energy nikalni hai.

---

Diagram:

Box ke beech mein V= 0 , aur dono sides (walls) par V= ♾.

x = 0 se x = a tak particle band hai.

---

"Let us consider a particle of mass 'm' confined in a one dimensional box of length 'a' and moving along x-direction."

→ Matlab ek particle jiska mass ‘m’ hai, ek 1D box mein band hai jiska length ‘a’ hai, aur wo sirf x-axis ke direction mein move karta hai.

---

"The walls of the box are formed by regions of high potential energy so that particles cannot escape."

→ Box ki deeware bahut high potential energy wali hain, isiliye particle unke bahar nahi nikal sakta.

---

"The potential energy outside the box will be infinite whereas inside the box its value will be zero."

→ Box ke bahar potential energy infinite hai, aur box ke andar zero hai.

---

"For the particle inside the box the value of x lies between 0 and a and the potential energy V = 0. Hence S.W.E is given by…"

→ Jab particle box ke andar hai, tab x ki value 0 aur a ke beech hoti hai, aur potential energy 0 hoti hai.

Is condition ke liye Schrödinger Wave Equation likhi jaati hai.

Comparison b/w the particle in 1-D box with a free particle

Or

What will happen if the walls of 1-D box suddenly removed

1. Particle in a 1D box (with walls)

• Jab ek particle ek 1D box of length a ke andar hota hai aur dono ends pe infinite potential walls hain,

  matlab particle bahar nahi ja sakta.

• Schrödinger equation solution deta hai standing waves (sine functions).

• Is condition ke wajah se boundary conditions apply hote hain → wavefunction zero hona chahiye at x=0 and x=a.

• Result: only some specific wavelengths fit → quantized energy levels:

E_n = \frac{n^2 h^2}{8 m L^2}, \quad n = 1,2,3,...

---

2. Ab question: “What if walls are suddenly removed?”

• Matlab ab particle ke paas koi restriction hi nahi hai, voh kahin bhi move kar sakta hai.

• Potential energy = 0 sab jagah.

• Schrödinger equation solution ab ek free particle wavefunction deta hai:

ψ= Asinkx + Bcoskx

yahaan koi bhi value le sakta hai (no restriction).

---

3. Kya hota hai energy ka?

Free particle ki energy hoti hai:

E = \frac{\hbar^2 k^2}{2m}

Important point: k koi bhi real value ho sakta hai → iska matlab hai ki energy bhi continuous hogi, discrete (quantized) nahi.

4. Conclusion

Jab box tha → quantized energy spectrum (discrete levels).

Jab walls hata diye → particle free hai → continuous energy spectrum.

---

💡 Simple analogy:

Imagine ek guitar string fixed ends pe — sirf kuch specific notes bajenge (quantized frequencies).

Ab string ke ends khol do → voh bas vibration karte rahenge kisi bhi frequency pe (continuous spectrum).

👉 Tumhare book ne isi ko short mai likha hai:

With walls → quantized energy levels.

Without walls → free particle → continuous energy.

Heisenberg Uncertainty principle

🔹 Heisenberg Uncertainty Principle kya kehta hai?

Yeh principle yeh batata hai ki ek particle (jaise electron) ki position aur momentum dono ko ek saath poori accuracy se measure karna impossible hai.

Agar tum uski position ko zyada accurately measure karne ki koshish karoge, to uska momentum uncertain ho jaata hai — aur agar momentum sahi se measure karoge to position uncertain ho jaayegi.

Yeh baat wave-particle duality se aati hai, matlab quantum level par electron kabhi wave jaise behave karta hai, kabhi particle jaise.

---

🔹 Wave–Particle Duality:

Quantum level pe objects (like electrons) ek saath wave aur particle dono ki tarah behave karte hain.

Toh inki exact position ya exact momentum ek hi waqt pe fix karna possible nahi hota.

---

🔹 Position aur Momentum:

Heisenberg ne yeh bataya ki agar hum kisi particle ki position bahut zyada accurately measure karein, toh momentum (yaani uska motion) uncertain ho jaata hai.

Aur agar momentum ko exact measure karein, toh position uncertain ho jaati hai.

Matlab — jitna ek cheez ko fix karoge, dusri utni hi uncertain ho jaayegi.

---

🔹 Mathematical Formula:

Formula hai:

Δx × Δp ≥ h / 4π

Yahaan:

Δx= position mein uncertainty

Δp = momentum mein uncertainty

h= Planck’s constant (6.626 × 10⁻³⁴ Js)

Iska matlab hai ki product of uncertainties hamesha h / 4π se zyada ya uske barabar hota hai.

Momentum p=mv hota hai, to formula likh sakte hain:

Δx × mΔv ≥ h / 4π

Δx × Δv ≥ h / 4πm

---

🔹 Example (Electron ke case mein):

Electron ka mass kg hota hai.

Agar hum electron ki position m (uske size ke barabar) tak accurately measure karte hain,

toh velocity (yaani speed) mein error m/s yaani 1000 km/s tak ho sakta hai!

Matlab agar hum position fix kar lete hain, toh velocity ka koi bharosa nahi rehta — bahut uncertain ho jaata hai.

---

🔹 Relevance to Quantum Mechanics:

Yeh principle humein quantum world ka asli nature samjhata hai —

ki particles deterministic nahi hote jaise classical mechanics ke objects (jaise ball ya car).

Unka behavior probability par based hota hai.

---

🔹 Not Applicable to Macroscopic Objects:

Yeh principle bade objects (jaise football, car, ya human body) par apply nahi hota,

kyunki unka mass bahut zyada hota hai — isliye uncertainty unke liye negligible hoti hai.

---

👉 Simple words mein:

Heisenberg ka principle kehta hai —

> “Tum kisi chhoti cheez (electron) ke baare mein ek hi waqt pe sab kuch nahi jaa sakte.

Agar tum uski jagah (position) sahi jaante ho, to tumhe uski speed (momentum) ka andaza nahi rahega —

aur agar tum uski speed jaante ho, to uski jagah uncertain ho jaayegi.”

Postulates of quantum mechanics

Quantum Mechanics ke Postulates (Siddhant)

Ye paanch postulates hain jo quantum mechanics ki foundation hain. Inhe prove nahi kiya ja sakta, bilkul jaise Newton ke laws ko prove nahi kiya ja sakta — bas experiment se confirm kiya ja sakta hai.

---

Postulate 1:

Kisi bhi system ki state ek wavefunction \psi(x, y, z, t) se describe hoti hai.

· Ye wavefunction system ki saari possible information ko contain karti hai.

· Matlab, agar aapko particle kahan hai, kaisi energy hai, etc. jaanna hai, toh \psi se nikalega.

---

Postulate 2:

Har physical property (jaise energy, momentum, position) ko quantum mechanics mein ek operator diya jaata hai.

· Operator matlab koi mathematical operation (jaise differentiate karna, multiply karna).

· Classical expression se operator banane ke liye:

· x ko x hi rakho

· p_x (momentum) ko \frac{h}{2\pi i} \frac{\partial}{\partial x} replace karo

· Example: Kinetic energy operator classical expression \frac{p_x^2}{2m} se banega:

\hat{K} = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2}

jahan \hbar = \frac{h}{2\pi}.

---

Postulate 3:

Jab aap koi physical property measure karte ho, toh result sirf eigenvalues a_i ho sakte hain jo equation se milte hain:

\hat{A} \psi_i = a_i \psi_i

\]

· Yahan \hat{A} uska operator hai, \psi_i eigenfunction hai, a_i eigenvalue hai.

· Matlab, measurement kabhi bhi kuch bhi result nahi dega — sirf allowed values (eigenvalues) hi aayenge.

---

Postulate 4:

Agar aap repeated measurement karte ho, toh uska average value ye hoga:

\langle A \rangle = \frac{\int \psi^* \hat{A} \psi \, d\tau}{\int \psi^* \psi \, d\tau}

\]

· Agar wavefunction normalized hai (yani \int \psi^* \psi \, d\tau = 1), toh denominator 1 hoga:

\langle A \rangle = \int \psi^* \hat{A} \psi \, d\tau

---

Postulate 5:

Wavefunction time ke saath change hoti hai time-dependent Schrodinger equation ke according:

\frac{i\hbar \partial \psi}{\partial t} = \hat{H} \psi

\]

· Yahan \hat{H} Hamiltonian operator hai (total energy ka operator).

· Ye equation batati hai ki wavefunction kaise evolve karegi.

---

Note:

In postulates ko samajhne ke liye examples dekhenge aage, lekin abhi bas ye jaano ki ye quantum mechanics ka base hain — jaise Newton’s laws classical mechanics ka base hain.