Sensitivity Analysis

Optimal Solutions

• deterministic assumptions in the data and relationships of a problem
• however, variables are sensitive and exposed to change

Sensitivity analysis

• used to examine the effects of changes in
(1) contribution rates for each variable,
(2) technological coefficients (the numbers in the constraint equations), and
(3) available resources (the right-hand-side quantities in each constraint).

• involves what if questions

Optimal Solutions

• deterministic assumptions in the data and relationships of a problem
• however, variables are sensitive and exposed to change

Sensitivity analysis

• used to examine the effects of changes in
(1) contribution rates for each variable,
(2) technological coefficients (the numbers in the constraint equations), and
(3) available resources (the right-hand-side quantities in each constraint).

• involves what if questions

Binding constraints

• obtaining additional units of that resource will result in higher profits
• no slack or surplus

Non binding constraint

• extra units available that are not being used
• obtaining additional units of that resource will not result in higher profits and will only increase the slack.

Changes in the Objective Function Coefficient

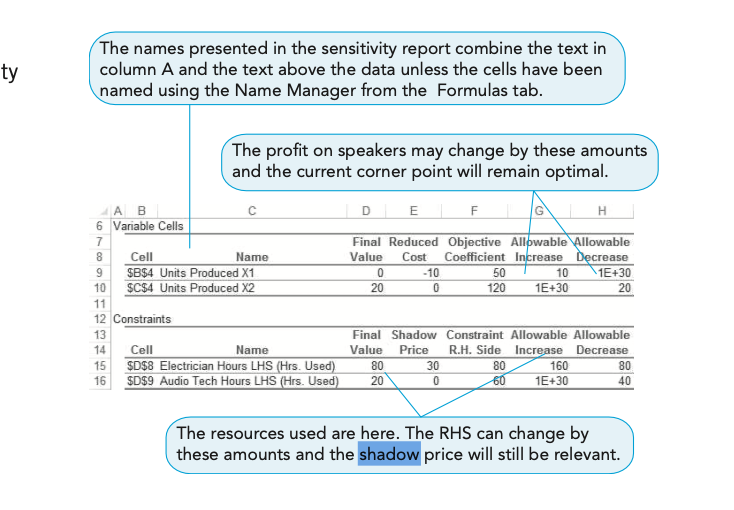
• within its upper and lower bounds, we can increase or decrease the objective function coefficient (profit) of any variable, and the current corner point may remain optimal
• go over range = new corner point

Upper and Lower bounds

• relate to changing only one coefficient at a time

Changes in the Technological Coefficients

• fewer or more resources are needed to produce a product coefficients in the constraint equations will change.
• no effect on objective function
• produce a significant change in the shape of the feasible solution region—and hence in the optimal profit or cost.

Changes in the Resources or Right-Hand-Side Values

• ____ values of the constraints often represent resources available to the firm.
• feasible region will change, and often the optimal solution as well

Shadow Price (max)

• aka dual prices
• improvement in the objective function value that results from a one-unit increase of a scarce resource in the right-hand side of the constraint.
• ex: The dual price of $30 per hour of electrician time tells us we can increase profit if we have more electrician hours.
• only relevant within its lower and upper bounds
• only for binding constraints
• for min problem: improvement in OF is a decrease (negative change); ___ is negative
• Exactly how much should a firm be willing to pay to make additional resources available?

Inter Sample

• decision variables
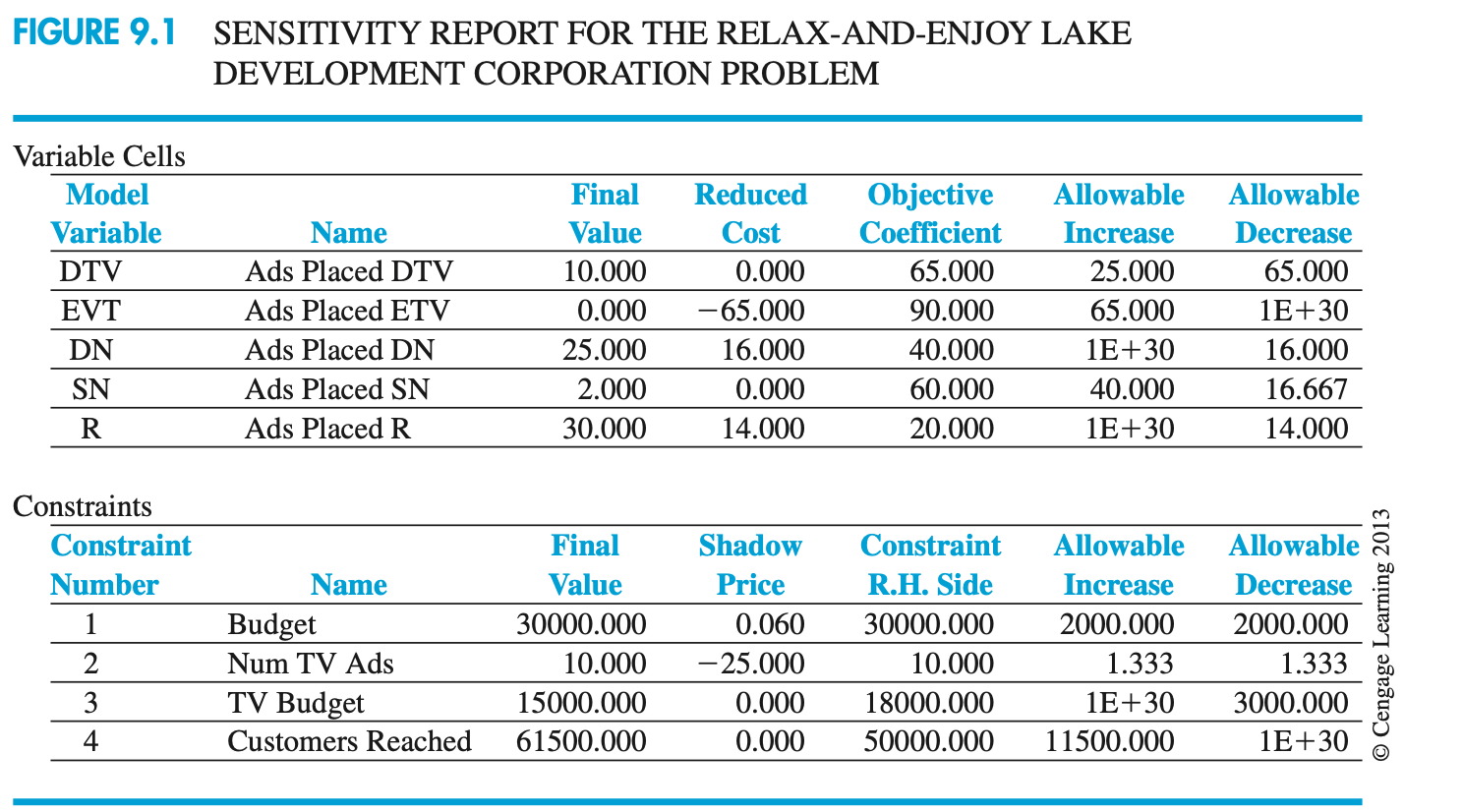
So, for example, the reduced cost of 65 for evening TV indicates that forcing the use of this type of ad would actually drop exposure quality by 65 points. On the other hand, allowing another daily newspaper ad (26 instead of a limit of 25) would increase exposure quality by 16 units.

• Constraints

Budget: Therefore, a $1.00 increase in the advertising budget will lead to an increase of 0.06 exposure quality units.

TV: The shadow price of 􏰇25.000 for the number of TV ads indicates that reducing the number of required television commercials by 1 will increase the exposure quality of the advertising plan by 25 units.