Probability - Stats Module 2

population is known

probability is used to describe the likelihood of observing a particular sample outcome

population is unknown

probability is used in making statements about the makeup of the population

experiment

process by which an observation or measurement is obtained

simple event

outcome observed on A SINGLE REPETITION of an experiment. e.g. a tossed coin turns up heads

sample space

the set of all simple events, usually denoted by the symbol S

event

collection of simple events

mutually exclusive events

when one event occurs, the other cannot, and vice versa

table of outcomes

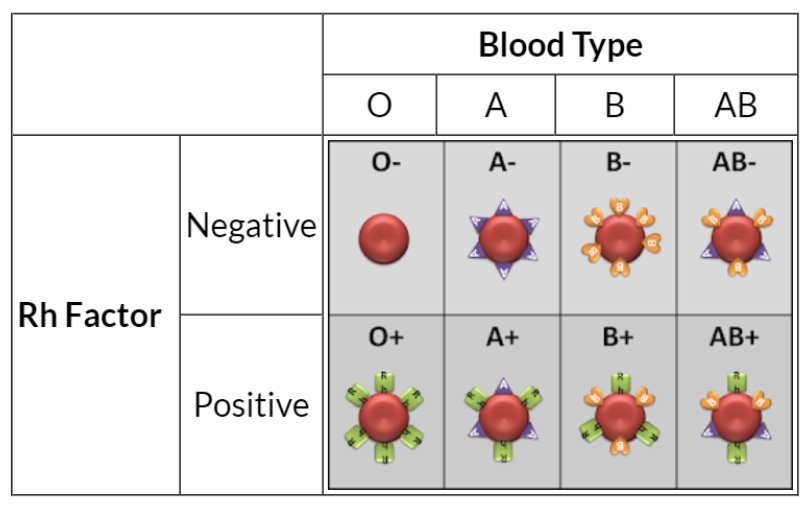
uniform probability model

P(A) = no. of simple events in A / no. of simple events in S

alternative:

in cases where the outcomes are not equally likely to occur, P(A) = P(A₁) + P(A₂) + … P(A_n)

basically if the simple events of A dont hold the same probability, just add the probabilities of individual simple events in A

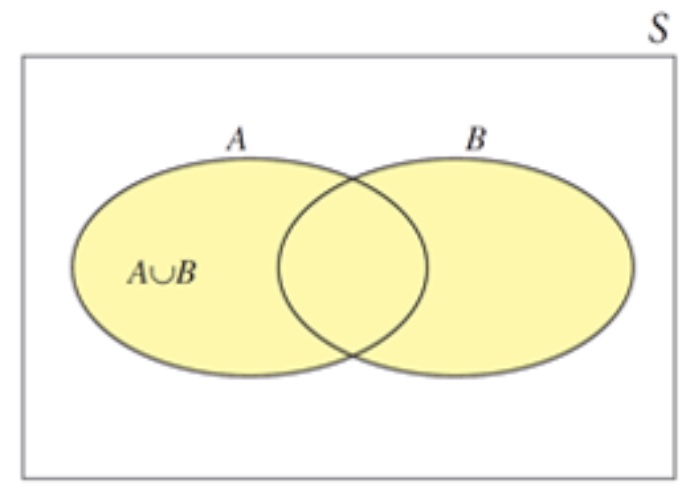
union

denoted by A U B, is the event of one of the ff

• A alone occurs

• B alone occurs

• both A and B occur

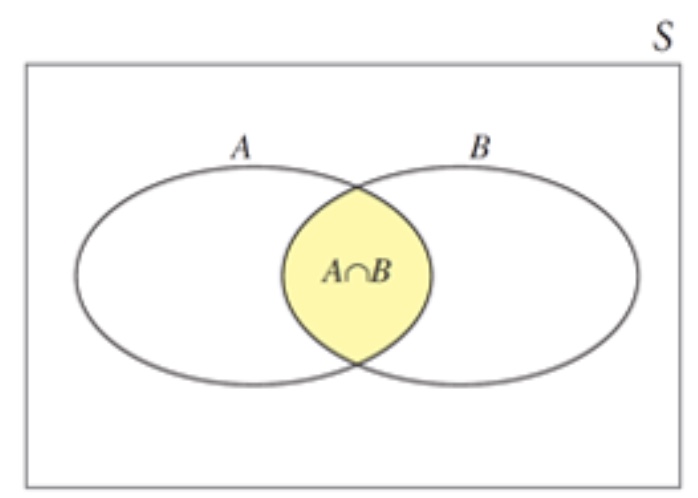
intersection

denoted by A ∩ B, is the event that BOTH A and B occur

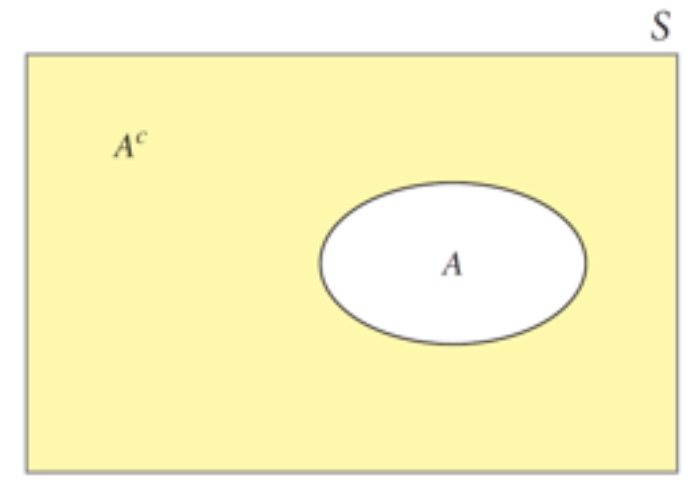
complement

denoted by A^c, is the event that A does NOT occur

note: it is not always the opposite. Be careful with determining the complement as it encompasses everything that happens when A does not happen. Sometimes, a simple negative, such as “does not” will do.

addition rule

Given two events, A and B, the probability of their union, A U B, is equal to

P (A U B) = P(A) + P(B) - P(A∩B)

complement rule

Given an event A, the probability of its complement A^C, is equal to

P(A^C) = 1 - P(A)

conditional probability

event A, GIVEN that a non-empty event B has occurred is

P (A | B) = P(A ∩ B) / P(B)

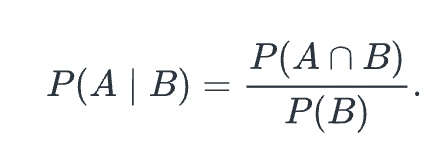
multiplication rule

P(A ∩ B) = P(A | B) P(B) or P(B | A) P(A)

ABB or BAA

independent events

• if the probability of A does not change given B, and vice versa. Events that are not ____ are dependent.

• if and only if P(A ∩ B) = P(A) P(B)

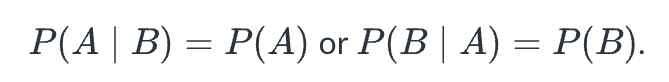
mutually independent

The events A₁, A₂, …A_n are _____ if each pair of events A_i and A_j are independent.

corollary 1

if two events A and B are independent, then A and B^C; A^C and B; A^C and B^C are independent.

corollary 2

The events A₁, A₂, … A_n are mutually independent if and only if P(A₁, A₂, …A_n) = P(A₁) P(A₂) … P(A_n)

mutually exclusive or disjoint

events cannot happen together when the experiment is performed. When A occurs, B cannot occur anymore, and conversely.

It follows that these are dependent.