AP Calculus things to rmb
0.0(0)Studied by 2 people
0%Unit 3: Differentiation: Composite, Implicit, and Inverse Functions Mastery
0%Exam Mastery
Build your Mastery score
Supplemental Materials
Card Sorting
1/24
Earn XP
Description and Tags
Limits and few deriv`atives for rn(will be updated)
Last updated 7:39 PM on 12/27/25
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
25 Terms
1
New cards
lim [sin(x)/x] =
1
2
New cards
lim [(cos(x)-1)/x] =
1
3
New cards
lim [sin(ax)/x] =
a
4
New cards
lim [sin(ax)/sin(bx)] =
a/b
5
New cards
d/dx[sin(x) ] =
cos(x)
6
New cards
d/dx[cosx] =
-sin(x)
7
New cards
d/dx[tanx] =
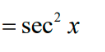
8
New cards
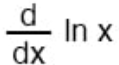
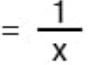
9
New cards
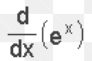
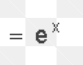
10
New cards
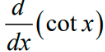
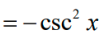
11
New cards
d/dx[secx]
(tan(x) )(sec(x))
12
New cards
d/dx[cscx]
(-cot(x))(csc(x))
13
New cards
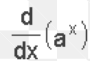
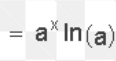
14
New cards
d/dx[logb(x)]
1/((ln(b))(x))
15
New cards
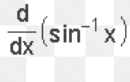
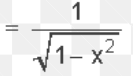
16
New cards
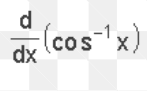
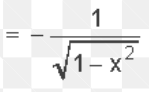
17
New cards
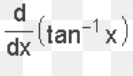
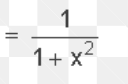
18
New cards
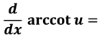
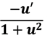
19
New cards
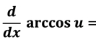
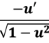
20
New cards
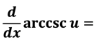
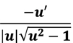
21
New cards
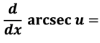
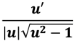
22
New cards
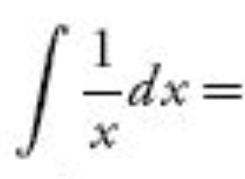
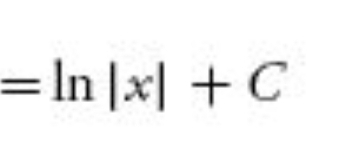
23
New cards
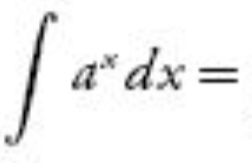
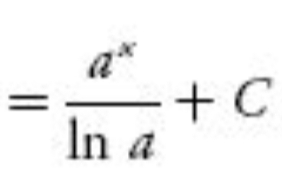
24
New cards

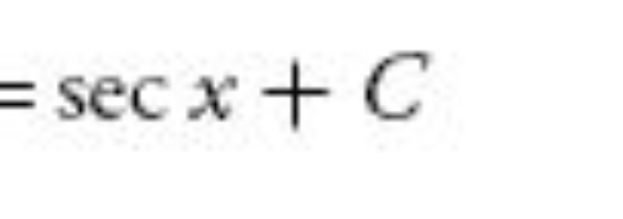
25
New cards