Toolkit

Standard form:

Some numbers are too big or too small to write easily, so we put them into standard form. In standard form, numbers are always written in the form $ax10^k$ where

• 1≤a≤10 (there must be one non-zero digit before the decimal point)

• k ∈ ℤ (k must be an integer)

• k > 0 for large numbers (how many times a is multiplied by 10)

• k < 0 for small numbers (how many times a is divided by 10)

Laws of indices:

These allow us to simplify and manipulate expressions involving exponents. The key index laws you need to know are:

• $(xy)^m$ = $x^m$ x $y^m$

• $(x/y)^m$ = $x^m$/$y^m$

• $x^m$x$x^n$ = $x^m$$^+$$^n$

• $x^m$/$x^n$ = $x^m$$^-$$^n$

• ($x^m$)$^n$ = $x^m$$^n$

• $x^1$ = $x$

• $x^0$ = 1

• 1/$x^m$ = $x^-$$^n$

• $x^1$$^/$$^n$ = n√x

• $x^m$$^/$$^n$ = n√$x^m$

These laws are NOT in the formula booklet.

Partial fractions:

These allow us to simplify rational expressions into the sum of two or more fractions with constant numerators, allowing for integration of rational functions.

Step 1: factorise the denominator into the product of two linear factors

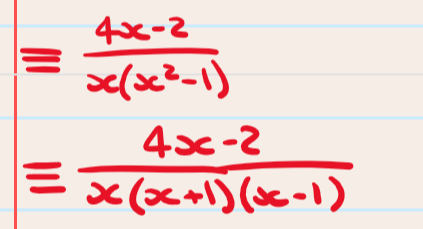Step 2: split the fraction into a sum of two fractions (use A, B and C to represent the unknown factors)

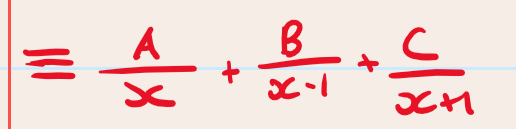Step 3: multiply through by the denominator to eliminate fractions

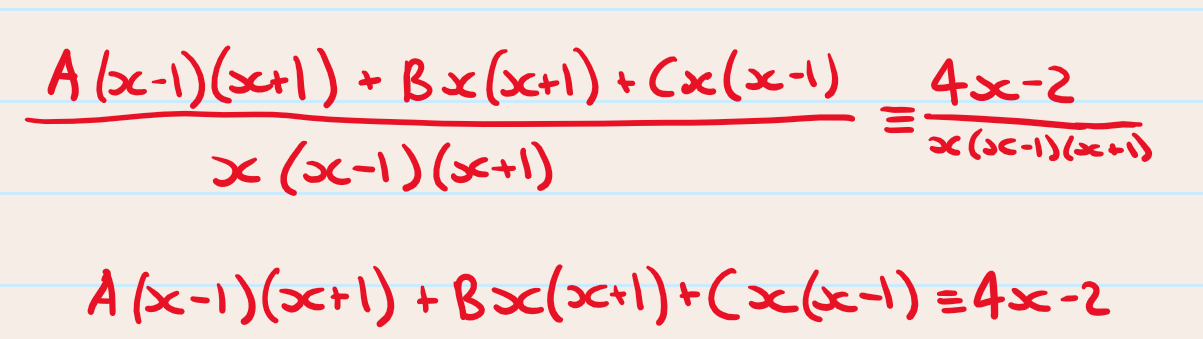Step 4: substitute values into the identity and solve for the unknown constants

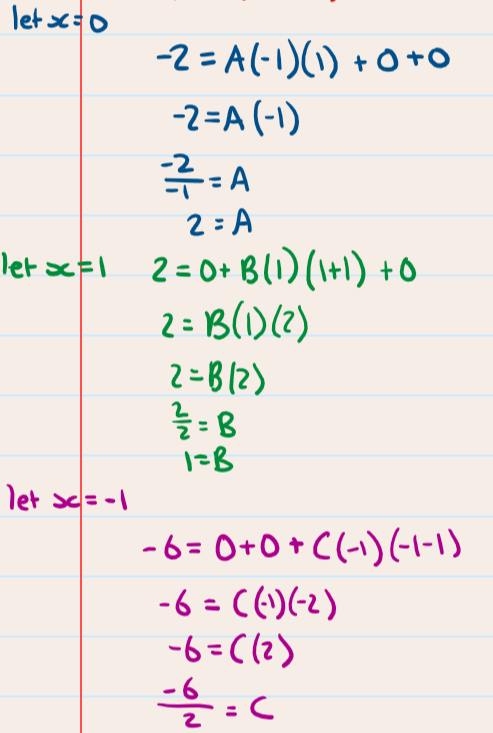Step 5: Write the original as partial fractions

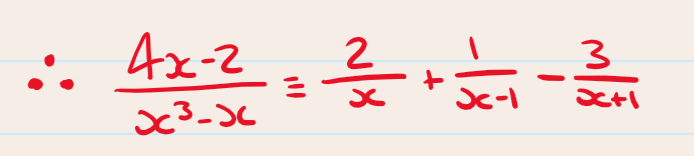
Exponentials and Logarithms

Logarithms:

A logarithm is the inverse of an exponent. If $a^x$=b, loga b = x. Two important cases to know are:

• $ln x$ = loge x

  • where e is the mathematical constant 2.718…

• log x = log10 x

The laws of logarithms (which are in the formula booklet) are equivalent to the laws of indices.

• loga xy = loga x + loga y

  • this relates to $a^x$ x $a^y$ = $a^x$$^+$$^y$

• loga x/y = loga x - loga y

  • this relates to $a^x$/$a^y$ = $a^x$$^-$$^y$

• loga $x^m$ = mloga x

  • this relates to ($a^x$)$^y$ = $a^x$$^y$

Sequences and Series

Arithmetic Sequences & Series:

In an arithmetic sequence, the difference between consecutive terms is constant. This constant difference is known as the common difference, d. An arithmetic constant can be increasing (positive common difference) or decreasing (negative common difference). The nth term formula for an arithmetic sequence is given as:

An arithmetic series is the sum of all of the terms in an arithmetic sequence given by the following formulas:

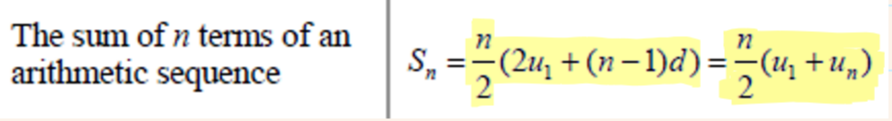Geometric Sequences & Series:

In a geometric sequence there is a common ratio, r, between consecutive terms in the sequence. the sequence can be increasing (r>1) or decreasing (0<r<1). If the common ratio is negative, the terms will alternate between being negative and being positive. The nth term formula for a geometric sequence is given as:

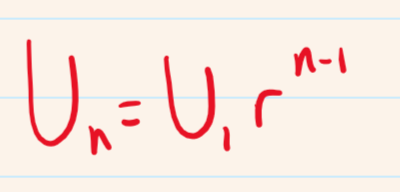A geometric series is the sum of a certain number of terms in a geometric sequence given by the following formulas:

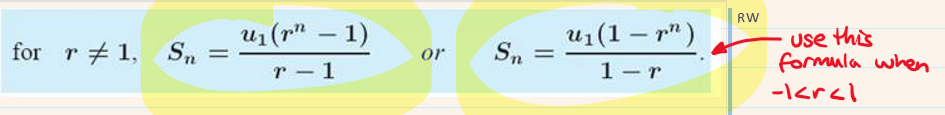Sum to Infinity:

A geometric sequence will either increase or decrease away from zero or the terms will get progressively closer to 0 (in this case it is said to converge). If |r| doesn’t converge (i.e. is larger than or equal to 1), we cannot find the sum to infinity. This is found using the formula:

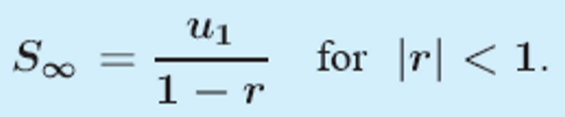
Proof

Language of Proofs:

You need to be familiar with the different sets of numbers:

• ℕ - the set of natural numbers

• ℤ - the set of integers

• ℚ - the set of quotients (rational numbers)

• ℝ - the set of real numbers

Proof by Deduction:

A proof by deduction question will often require showing that a result is true for all integers, consecutive integers or even or odd numbers.

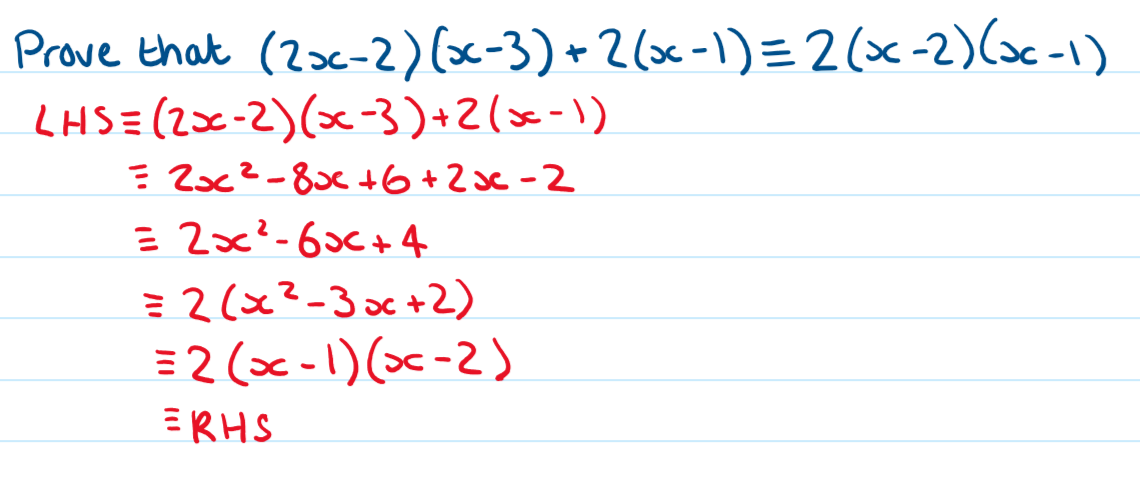Proof by Induction:

This is a way of proving a result is true for a set of integers by showing that if it is true for one integer than it is true for the next integer. It is important that you set this up correctly, following the steps below, to gain full marks on these questions.

Proof by Contradiction:

Proof by contradiction is a way of proving that a result is true by showing that the negation (opposite) of the result is not true. Examples of negation can be found below:

An example of a question (and the working out) are below:

Binomial Theorem

Binomial Theorem:

The binomial theorem gives a method for expanding a two-term expression raised to a power. This can be done using the formula:

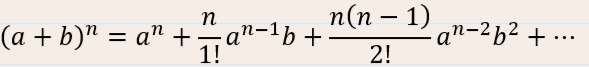Where:

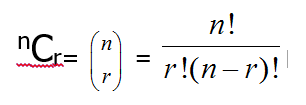We can also use the binomial theorem for fractional and negative indices by using the formula below:

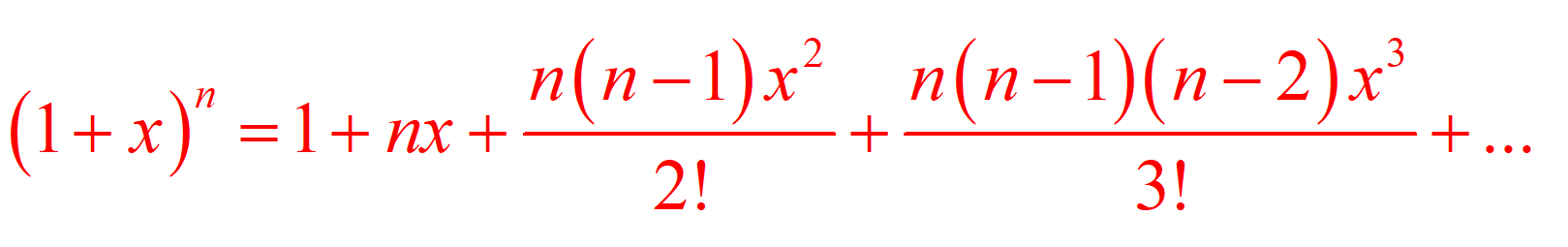
Permutations and Combinations

Permutations:

A permutation is the number of possible arrangements of a set of objects when the order of the arrangement matters. You can find the value of a permutation easily using your GDC.

Combinations:

This is the number of possible arrangements of a set of objects when the order of the arrangement does not matter.

Complex Numbers

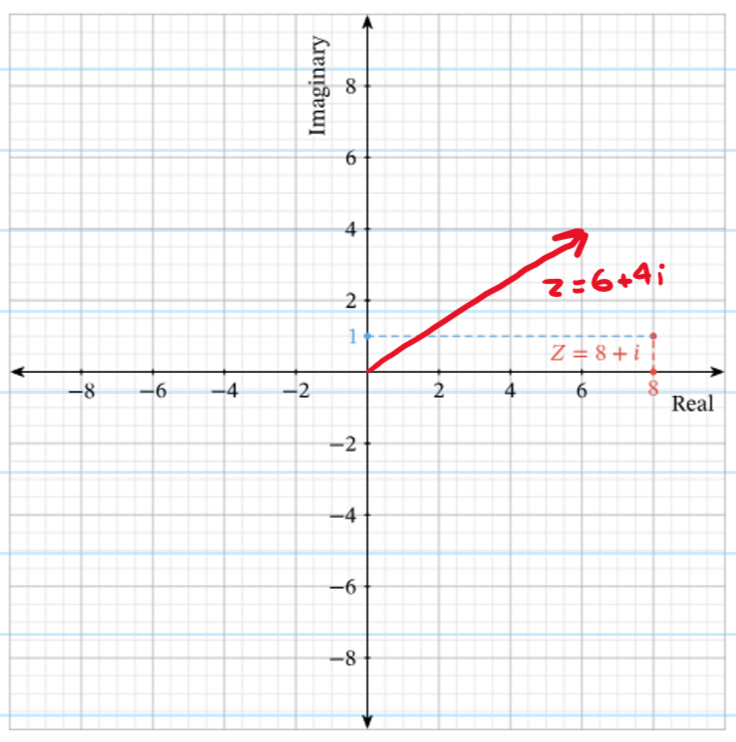
Argand Diagram:

This is also sometimes known as the complex plane and we use it to illustrate complex numbers. It has two axes, the real axis (x-axis) and imaginary axis (y-axis). Complex numbers are often represented as vectors, with an arrow away from the origin. This allows for geometrical representations of complex numbers.

Cartesian Form:

This is one of the forms that we can write complex numbers in. Cartesian form is when we write it as z = a + bi, where a, b ∈ ℝ. In general for z = a + bi, a = Re(z) and b = Im(z).

To add or subtract numbers in Cartesian Form, simplify the real and imaginary parts separately. For example:

ADDITION: (a + bi) + (c + di) = (a + c) + (b + d)i

SUBTRACTION: (a + bi) - (c + di) = (a - c) + (b - d)i

We can also multiply numbers in Cartesian form. They can be multiplied by a constant just like algebraic expressions or by each other like two linear expressions. REMEMBER: i² = -1.

MULTIPLICATION BY A CONSTANT: k(a + bi) = ka + kbi

MULTIPLICATION: (a + bi) x (c + di) = ac (ad + bc)i + bdi² = ac + (ad + bc)i - bd

It is also important that you know the value of i to higher powers

• i² = -1

• $i^3$ = i² x i = i x (-1) = -i

• $i^4$ = i² x i² = (-1) x (-1) = 1

• $i^5$ = i² x i³ = (-1) x (-i) = i

• $i^6$ = i³ x i³ = (-i) x (-i) = i² = -1

To be able to divide complex numbers, you must use the complex conjugate to change the denominator to a real number. This complex conjugate is z* = a - bi

• if z = a - bi, z* = a + bi

• z + z* is always real

  • (a + bi) + (a - bi) = 2a

• z - z* is always imaginary

  • (a + bi) - (a - bi) = 2bi

• z x z* is always real

  • (a + bi) x (a - bi) = a² + b²

Then to divide complex numbers, follow these steps:

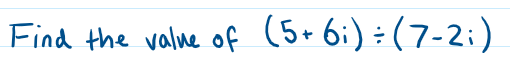Step 1: express the calculation in the form of a fraction

Step 2: multiply the numerator and the denominator by the conjugate of the denominator

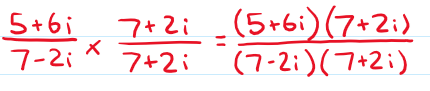Step 3: multiply out and simplify your answer

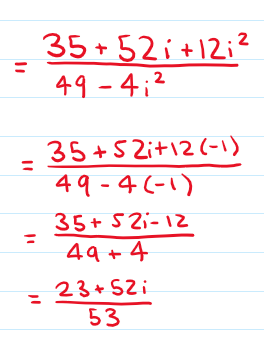Step 4: write your answer in Cartesian form as two terms simplifying them if needed

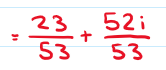Modulus and Argument:

The modulus of a complex number is its distance from the origin when plotted on an Argand diagram. The modulus of z is written as |z|. If z = x + iy, we can use Pythagoras’ Theorem to show that |z| = √x² + y². A modulus is never negative.

The modulus is related to the conjugate, z*, by:

• zz* = z*z = |z|²

  • because zz* = (x + iy)(x - iy) = x² + y²

The argument of a complex number is the angle that it makes on an Argand diagram. The angle must be taken from the positive real axis and must be measured in a counter-clockwise direction. Arguments are measured in radians and can be given in terms of π. The argument of z is written as arg z. They can be calculated using right-angled trigonometry and are usually in the range -π < arg z ≤ π.

• Negative arguments are for complex numbers in the third and fourth quadrants.

• The argument of 0, arg 0, is undefined (as no angle can be drawn).

When two complex numbers are multiplied their moduli are also multiplied and their arguments are added. When they are divided, their moduli are also divided and their arguments are subtracted.

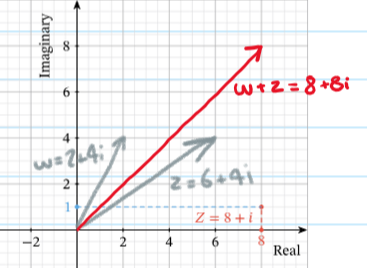
Geometry of Complex Addition and Subtraction:

This is what addition looks like on an Argand diagram:

And this is what subtraction looks like:

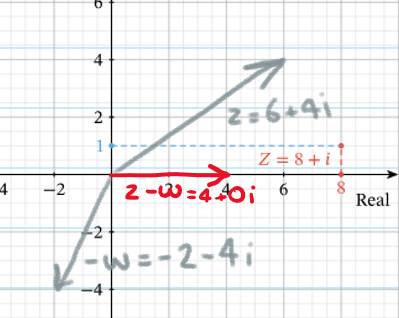The rules of the geometric representations of addition and subtraction of complex numbers (assuming w=a + bi) are:

• adding w to z results in z being translated by:

• subtracting w from z, results in z being translated by:

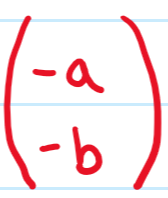
When we multiply by a complex number by a real number, a, there will be an enlargement of the vector by scale factor a. For positive values of a the direction of the vector will not change, only the distance of the point from the origin.