BST260 midterm 2

how would you generate a sample of n draws from the values of 1-365, where multiple draws can take the same number 

sample(365, n, replace=TRUE)

what does this do, assuming that same_birthday is a function that returns true if any of the n draws are the same. replicate(B, same_birthday(50))

it draws 50 values from 1-365 without replacement. This is one trial. It then does this process B times. So it will return B 0s (no same birthday) or 1s (same birthday0

what is the probability, exactly, of each of n people having different birthdays?

1 x (364/365) x (363/365) x … x (365-n+1)/365

The probability of landing on a green slot is 1/19. The payout for winning on green is \$17 dollars. This means that if you bet a dollar and it lands on green, you get \$17. If it lands on red or black you lose your dollar. Create a sampling model to simulate the random variable $X$ representing the casino's profit from a single \$1 bet on green. Use the sample function.

n=1

x <- sample(c(-17, 1), n, replace = TRUE, prob = c(1/19, 18/19))

9. Now create a random variable $S$ of the Casino's total winnings if $n = 1,000$ people bet on green. Use Monte Carlo simulation with B=10,000 trials to estimate the probability that the Casino loses money.

Hint you will use the same line in the previous question but within a function

n <- 1000

B<- 10000

S <- replicate(B, {

x <- sample(c(-17, 1), n, replace = TRUE, prob = c(1/19, 18/19))

sum(x)

})

What is the expected value of X, the casino’s profit from a single $1 bet? This will be in pure math 

E[X] = -17 \cdot (1/19) + 1 \cdot (18/19)
E[X] = 0.052

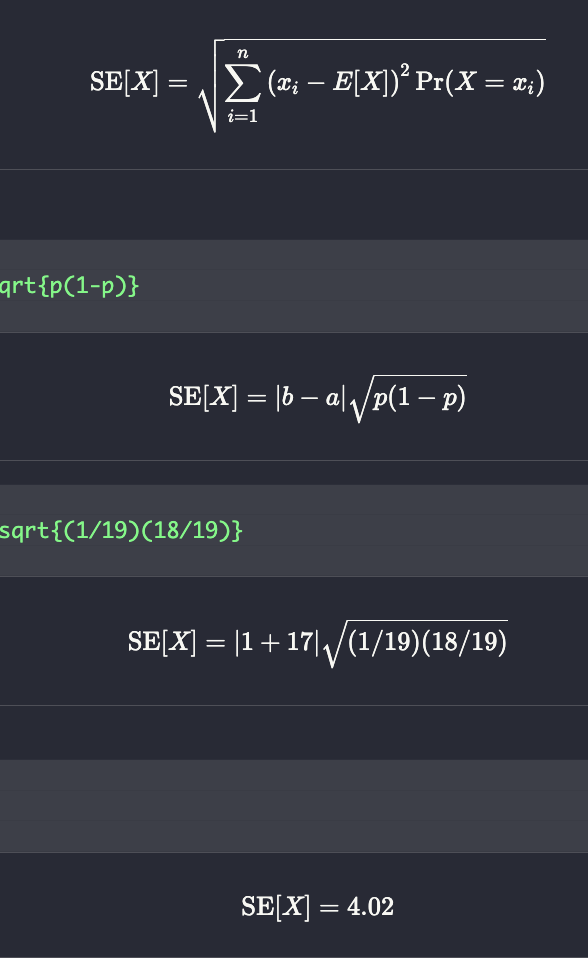
What is the standard error of X?

picture

How would find the expected value of S, the casino’s winnnings after 1,000 $1 bets?

E[S] = number of draws x average

E[S] = 1000 × 52 = 52

What is the standard error of S?

picture

Find the approximate probability using the CLT that S is less than 0

pic

What is the minimum number of people 𝑛 who must bet on green for the Casino to reduce the probability of losing money to 1%? Find this using the CLT

pic