12-06: Geometric Vectors

Vectors

Scalar: a quantity that @@describes magnitude or size only@@ (with or without units) @@but does not include direction@@
- Magnitude, no direction
- Magnitude: a number/numerical value is associated
- e.g. mass (2 kg), speed (2 km/hr)
Vector: a @@quantity that has both magnitude and direction@@
- Magnitude and direction
- Direction: where it is going
- e.g. velocity (2 km/hr west)

Vectors can be represented as:

The magnitude of a vector is designated using absolute value brackets

A vector’s direction can be expressed using many different methods

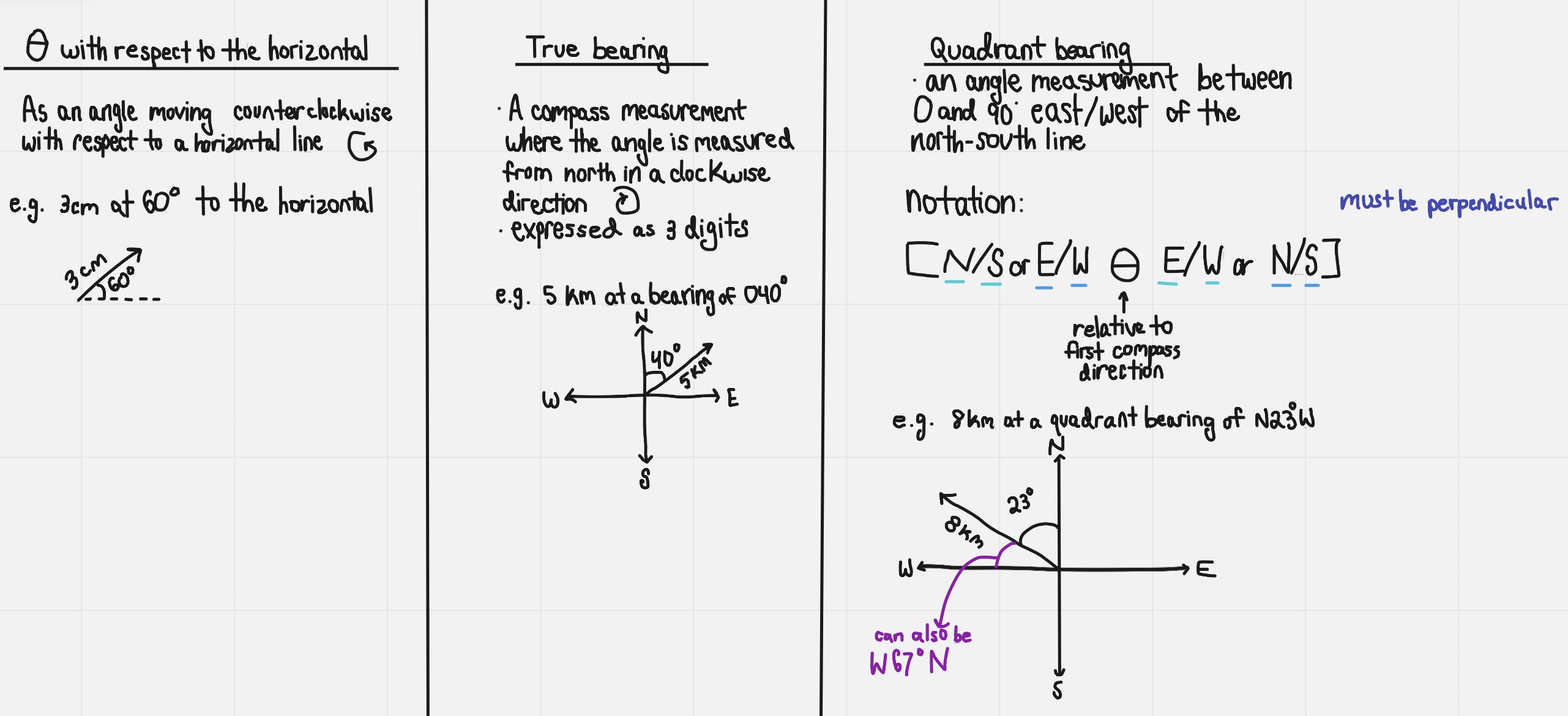
Parallel Vectors

Parallel vectors: have the same or opposite direction, but not necessarily the same magnitude
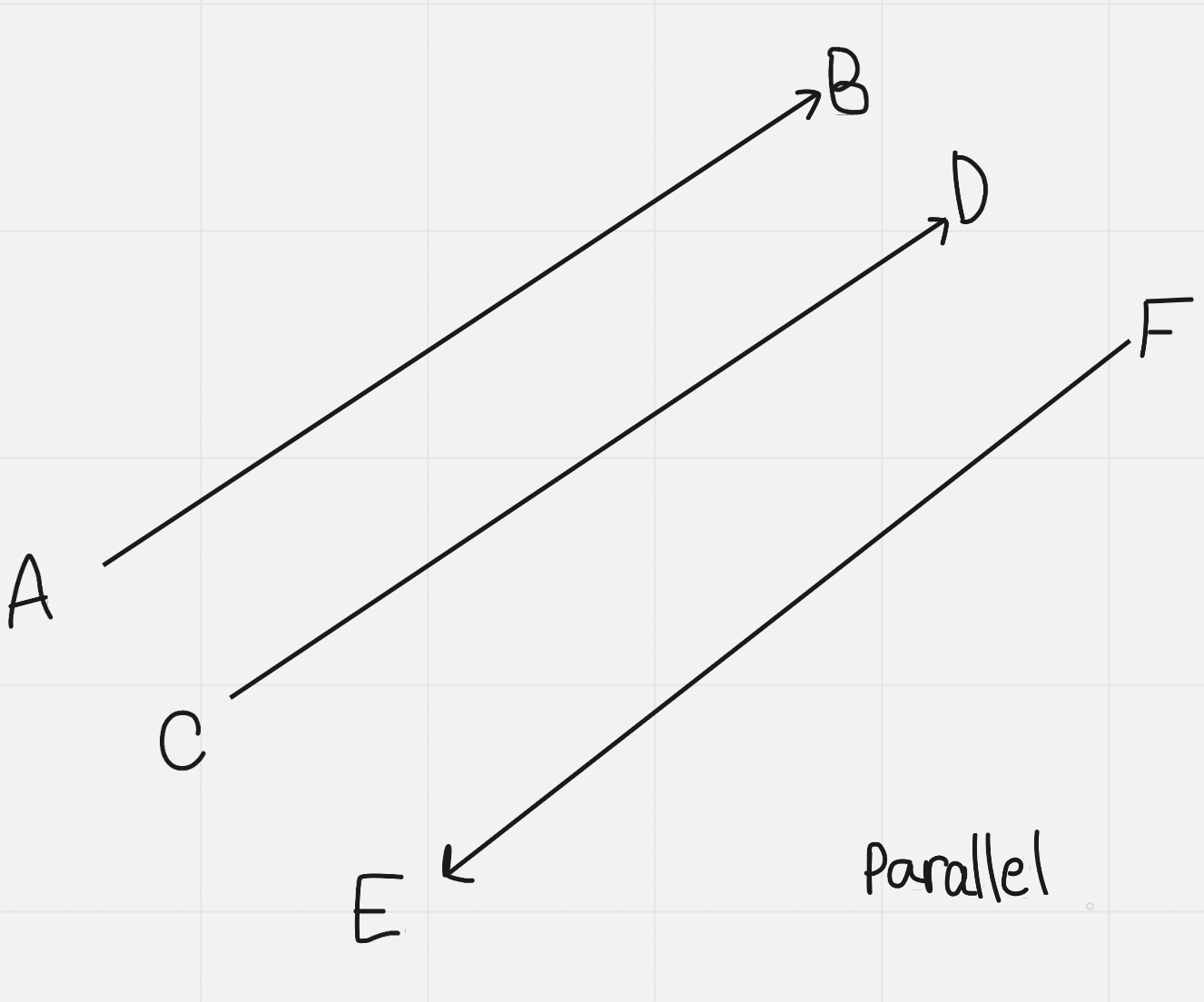Equivalent vectors: have the same magnitude and the same direction
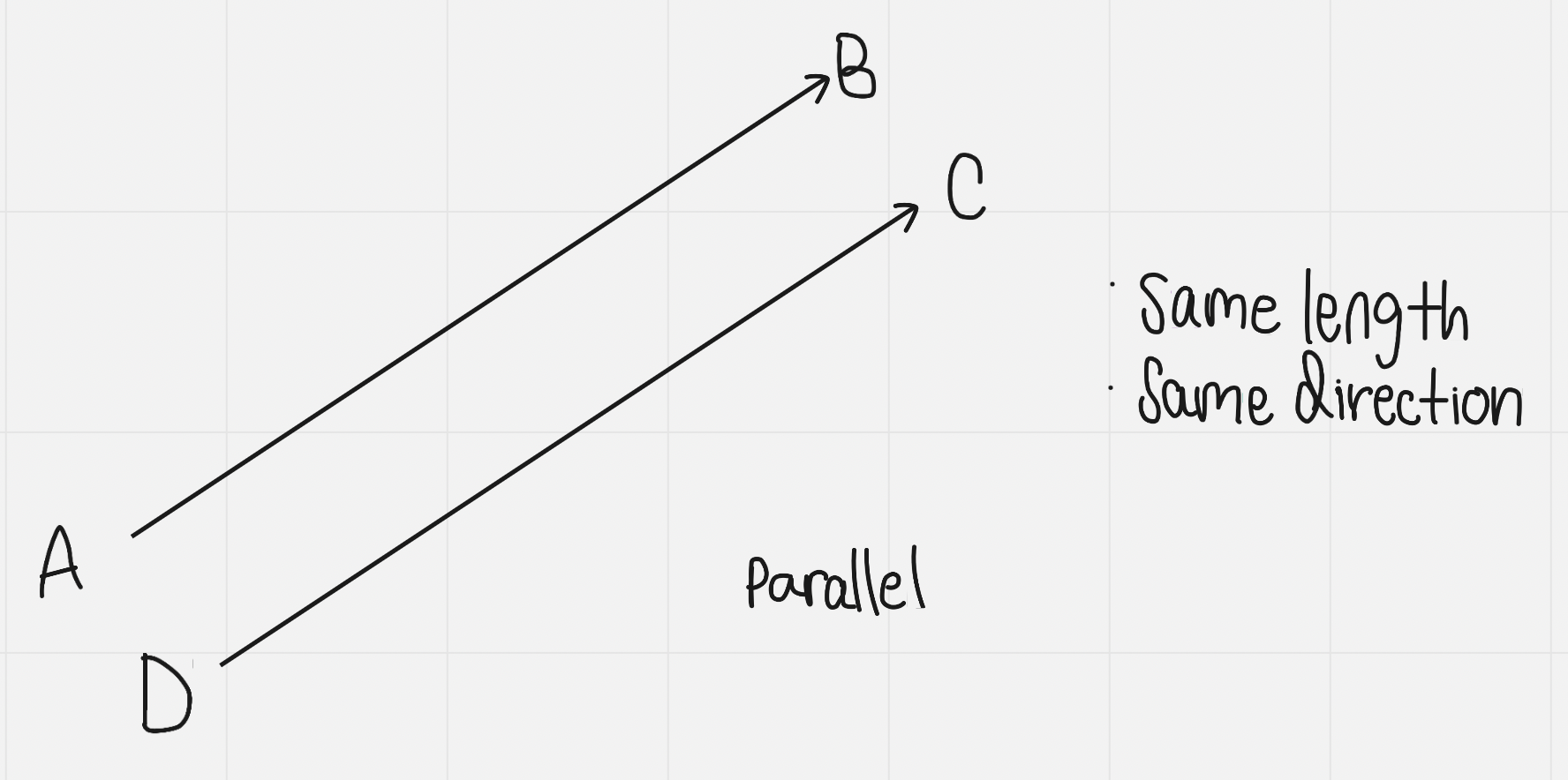Opposite vectors: have the same magnitude but opposite direction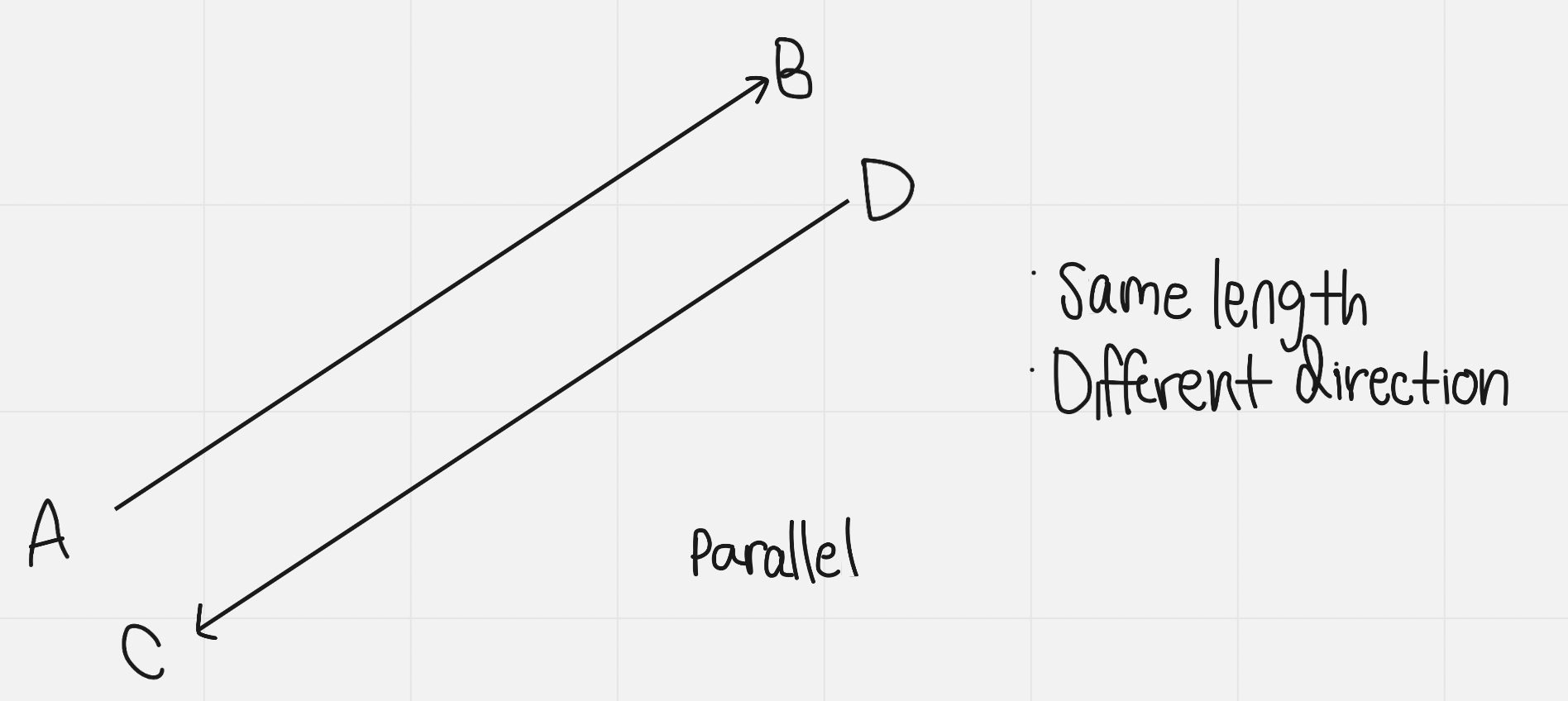
Multiplying a vector by a negative means that the direction gets flipped (or you could also say that its origin point gets flipped)

Addition & Subtraction of Vectors

When you add 2 or more vectors, you are finding a single vector called the ^^resultant^^

Think of adding vectors as finding a shortcut, it accomplishes the same thing that the original vectors did when applied one after the other

Adding Vectors

2 methods to adding vectors:

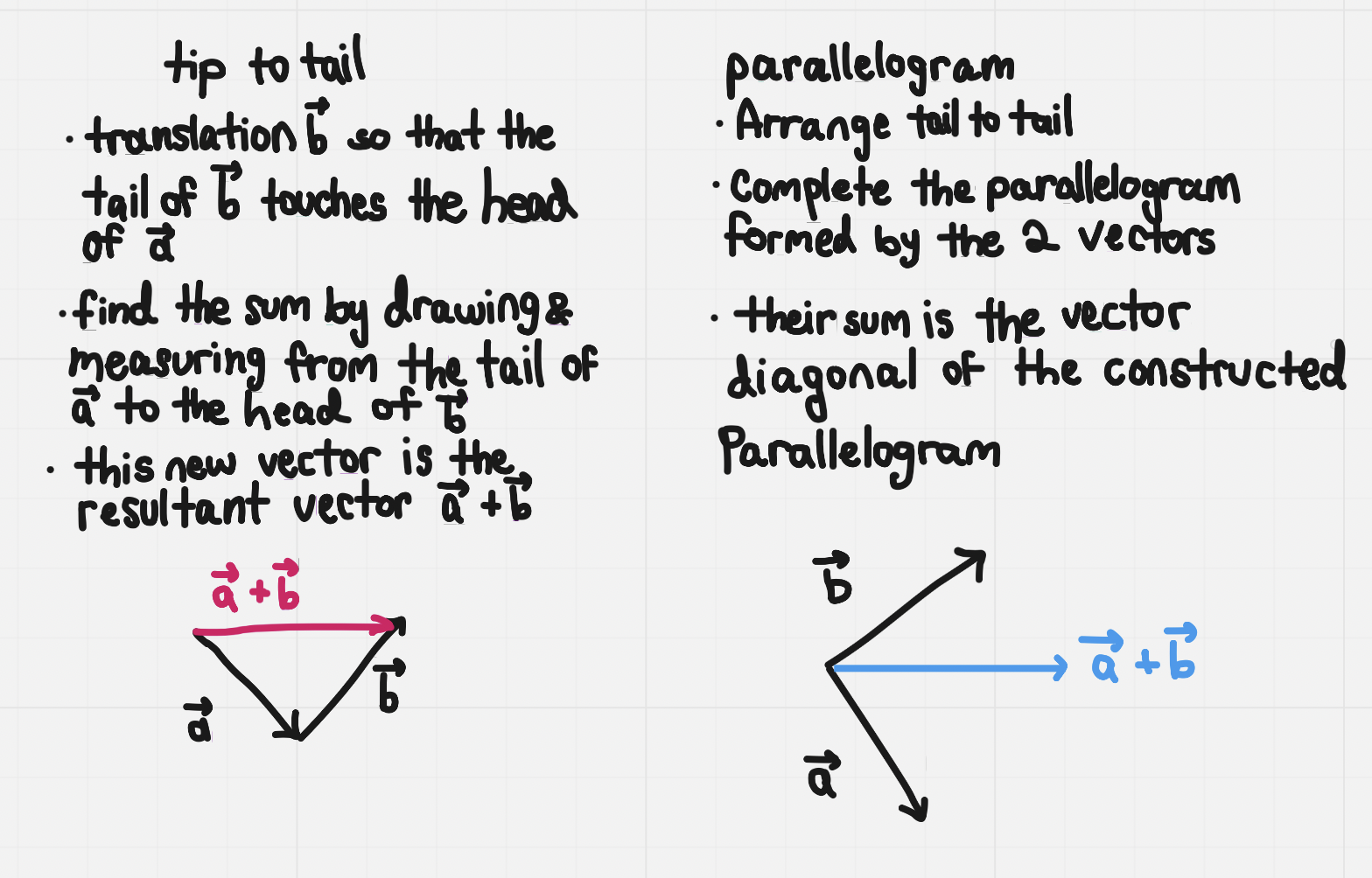
Subtracting Vectors

To subtract c-d, add the opposite of d to c

2 methods to subtracting vectors:

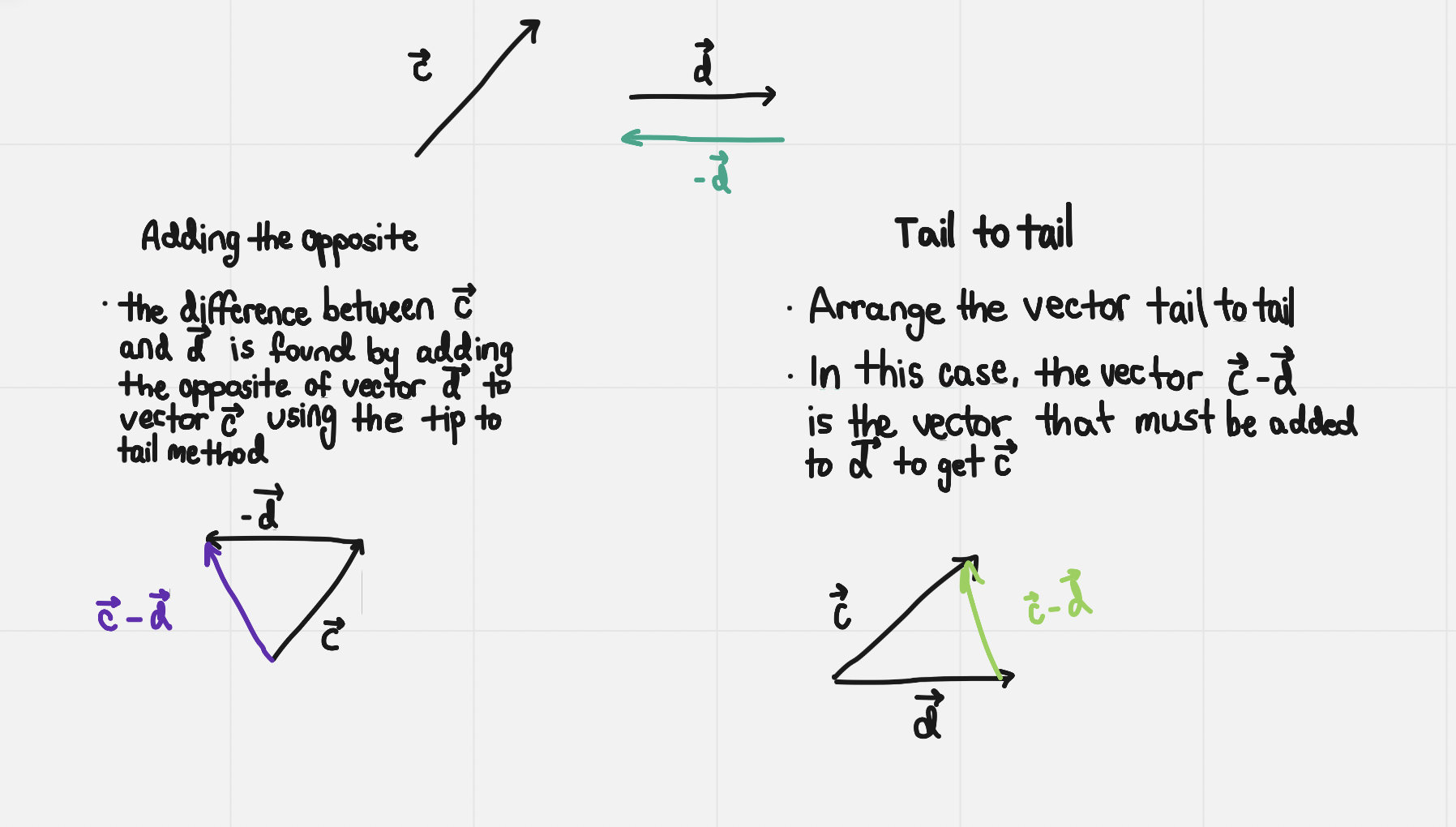Parallel vectors:

If ^^2 vectors are parallel and acting in the same direction^^, the ^^overall magnitude^^ is equal to: the ^^sum of the individual vectors^^ (use simple addition)

If %%2 vectors are parallel but acting in opposite directions,%% the %%overall magnitude%% is equal to: the %%difference of the two individual vectors%% (use simple subtraction)

Zero vector: when two opposite vectors are added together, the resultant has zero magnitude and no specific direction. Written as

Properties of Vector Addition

Multiplying a Vector by a Scalar

We can multiply a vector by a number k to produce a new scalar multiple of the vector
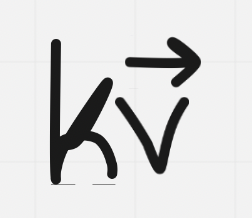
k is used as multiplication and is called a scalar, it can be any real number
%%Multiplying a vector by a scalar k can impact the vector’s magnitude & direction%%

Rules:

If %%k>0,%% then (vector) kv has the %%same directio%%n as (vector) v

If ^^k<0^^, then (vector) kv has the ^^opposite direction^^ as (vector) v

If 0<|k|<1, then the vector is decreased in magnitude, shortened

If ==|k| > 1, then the vector is increased in magnitude==, lengthened

If @@k=0, then the result is a zero vector@@

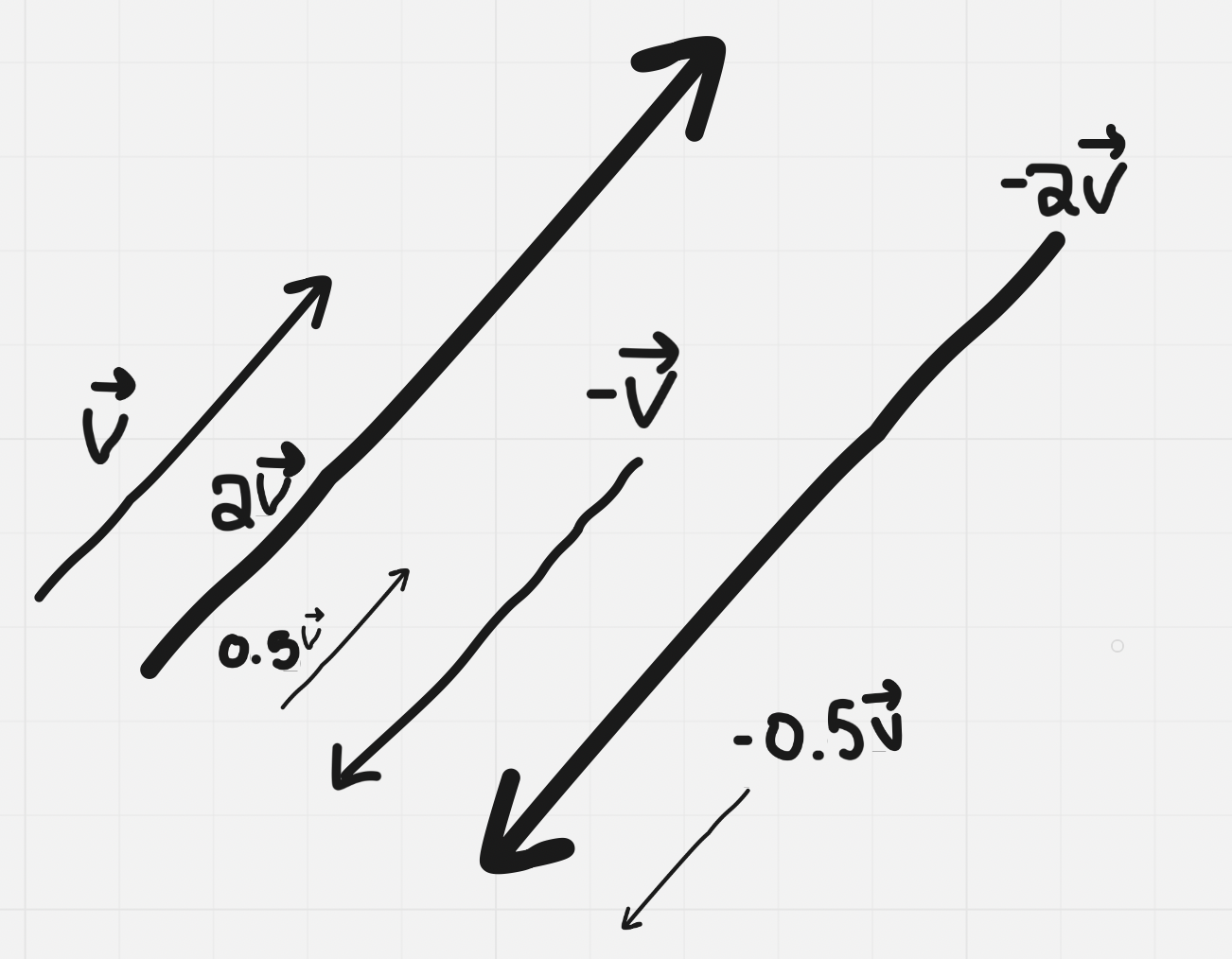Vectors that are scalar multiples are parallel and are said to be colinear. They form a straight line when arranged tip to tip

Vector properties for scalar multiples

Distributive property
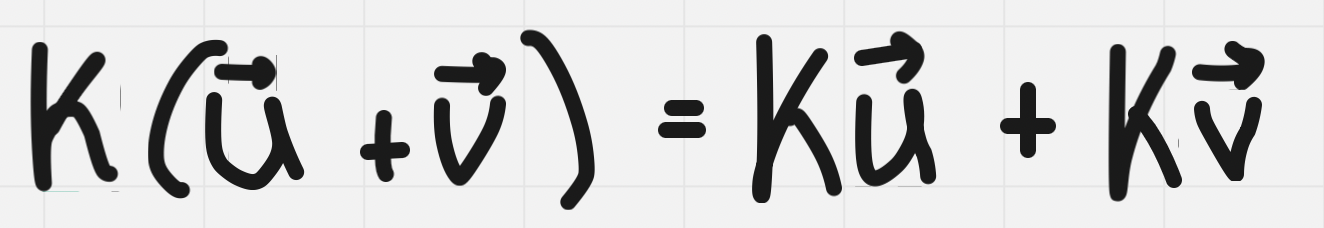
Associate property
Identity property

Applications of Vector Addition

RULE	FORMULA	WHEN TO USE
Pythagorean	a² + b² = c²	Right triangles, when given 2 sides and looking for a 3rd side
SOH CAH TOA	sinϴ = opp/hyp, cosϴ = adj/hyp, tanϴ=opp/adj	Right triangles, given an angle and a side & finding a side or 2 sides given and finding an angle
Sine law	a/sinA = b/sinB = c/sinC or sinA/a = sinB/b = sinC/c	Non right triangles, 2 sides and opp angle finding angle or given 2 angles opp side finding side
Cosine law	a² = b² + c² - 2bccosA or cosA = (b² + c² - a²)/2	Non right triangles, given 2 sides and enclosed angle finding 3rd side or given all 3 sides and finding angle

Resolution

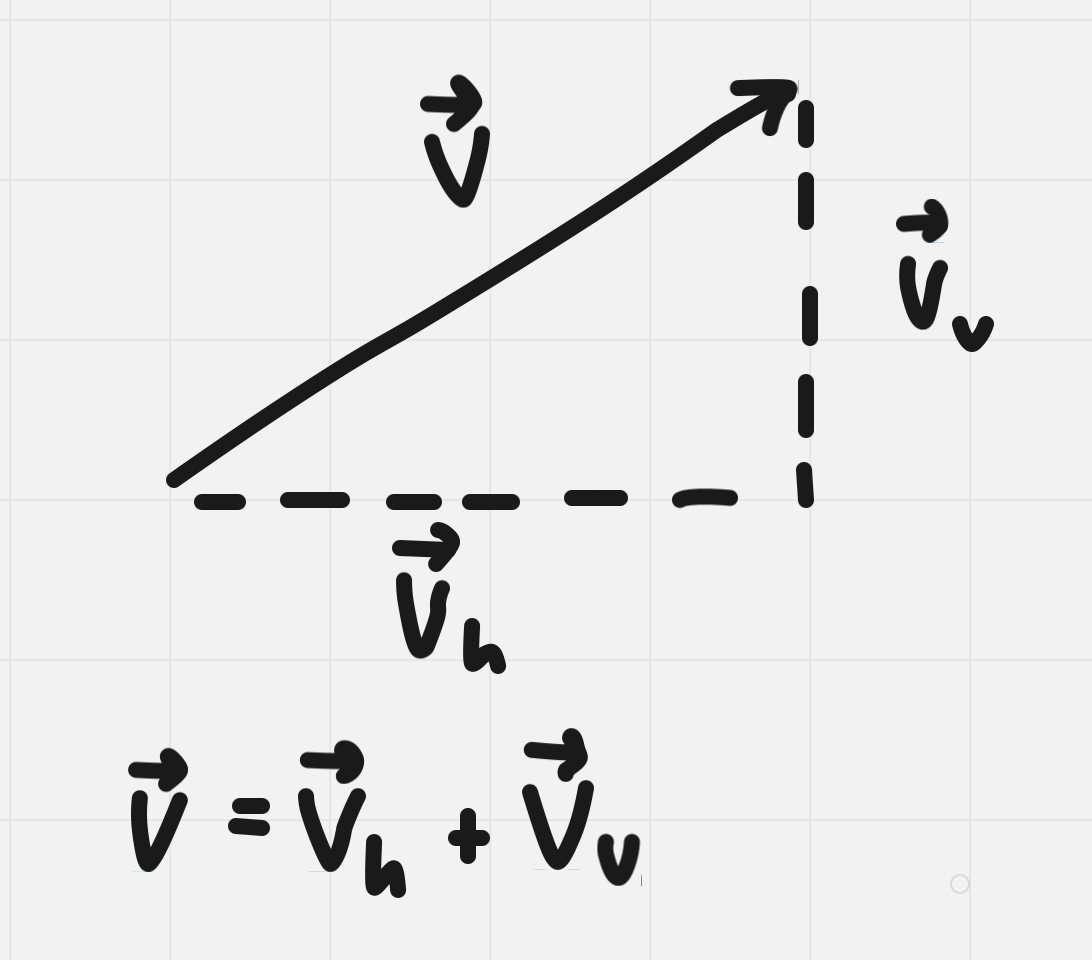
@@Resolution: taking a single force and decomposing it into 2 components@@
Most useful and important way to resolve a force vector occurs when this vector is resolved into 2 components that are at right angles to each other
A vector can be resolved into 2 perpendicular vectors whose sum is the given vector

Rectangular components of vectors: 2 perpendicular vectors that are added to give a resultant

Equilibrant vector: one that balances another vector/combination of vectors. Equal to the magnitude but opposite in direction to the resultant vector

If the equilibrate is added to a given system of vectors, the sum of all vectors including the equilibrant is a zero vector