Vector Spaces: Definitions, Operations, and Axioms in Linear Algebra

What is a vector space?

A nonempty set V of objects that is closed under operations ⊕ and ⊙, satisfying specific axioms.

What operations define the manipulation of objects in a vector space?

The ⊕ (o-plus) operation and the ⊙ (o-dot) operation.

What does the ⊕ operation do?

It defines an object x ⊕ y from two objects x, y ∈ V, typically representing vector addition.

What does the ⊙ operation do?

It defines an object α ⊙ x from an object x ∈ V and a real number α ∈ R, typically representing scalar multiplication.

What are the closure conditions for a set V under operations ⊕ and ⊙?

(C1) x ⊕ y ∈ V for any x, y ∈ V; (C2) α ⊙ x ∈ V for any α ∈ R, x ∈ V.

What is the significance of closure in vector spaces?

It guarantees that linear combinations of vectors remain within the set V.

What does Axiom A1 state?

x ⊕ y = y ⊕ x, which is the commutativity of ⊕.

What does Axiom A3 state?

x ⊕ 0V = x, indicating the existence of a unique zero vector 0V in V.

What does Axiom A4 state?

x ⊕ (−x) = 0V, meaning every vector x has a unique additive inverse −x.

What is an example of a vector space using real n × 1 vectors?

The set V = Rn with standard operations of addition and scalar multiplication.

What is an example of a vector space using polynomials?

The set V = Pn of polynomials of degree less than n, equipped with powerwise sum and scalar multiplication.

What is an example of a vector space using continuous functions?

The set V = C([a, b]) of all real-valued functions defined and continuous on the interval [a, b].

What is the result of the operation α ⊙ x for a vector x?

It scales the vector x by the scalar α, producing a new vector.

What is the significance of the operations ⊕ and ⊙ being consistent?

It ensures that the operations behave predictably, such as x ⊕ x = 2 ⊙ x.

Can a set be a vector space with different operations?

Yes, a set may be a vector space with one choice of operations but not with another.

What does it mean for a vector space to be 'closed' under an operation?

It means that performing the operation on any elements of the set results in an element that is also in the set.

What is the zero vector in the context of vector spaces?

The unique vector 0V that acts as the additive identity in the vector space.

What is a linear combination of vectors?

An expression formed by multiplying vectors by scalars and adding the results.

What is the role of scalars in vector spaces?

Scalars are real numbers used to scale vectors through the operation ⊙.

What is the additive inverse of a vector x?

The vector −x such that x ⊕ (−x) = 0V.

What does Axiom A6 state?

(α + β) ⊙ x = (α ⊙ x) ⊕ (β ⊙ x), which is the distributivity of scalar multiplication w.r.t. vector addition.

What does Axiom A8 state?

1 ⊙ x = x, indicating that 1 is the neutral value for scalar multiplication.

What happens if the closure conditions are not satisfied?

The set does not qualify as a vector space.

A5

Associativity of scalar

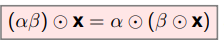
A6

Distributivity of scalar multiplication

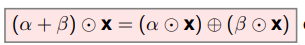
A7

Distributivity of multiplication w.r.t. ⊕

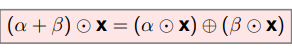
A8

1 is Neutral value for ⊙.