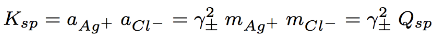Basic Thermodynamics II

Exp. 2 - Silver Equilibrium

ideal dilute solutions

Solutions for which the solute obeys Henry’s law and the solvent obeys Raoult’s law

Henry’s law

p_B = X_BK_B

in very dilute solutions, the vapor pressure of the solute is proportional to its mole fraction

Henry’s Law solute chemical potential

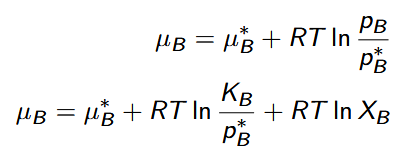
chemical potential of a solute in an ideal dilute solution 

μ^† = μ^∗_B + RT ln K_B /p^∗_B

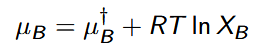
activity, a_i

accounts for deviations from ideal behavior of solutions

a_A = p_A / p^∗_A

activity coefficient, γ_i

quantifies the degree to which the solution is non-ideal, or it measures the extent to which the effective concentration is different from the true concentration, Xi; depends on the composition, molality, and temperature of the solution

a_i = γ_iX_i

μ = μ◦ + RT ln a

a = γm

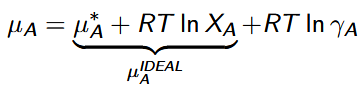
activity coeffecient for solvent

γ_A → 1 as X_A → 1 at all temperatures and pressures.

activity coeffecient for solute

γ_B → 1 as X_B → 0 at all temperatures and pressures.

Electrolytes

exist as solvated positive and negative ions; quite different from the ideal and real (nonelectrolyte) solutions of neutral solutes

electron interactions

Coulomb interactions between ions in an electrolyte solution are so strong that approximation of replacing activities by molalities is valid only in very dilute solutions (< 10⁻³ mol kg⁻¹ in total ion concentration)

chemical potential of electrolyte solute

Mp Xq (s) H2O → pMz+ (aq) + qX z− (aq)

pz+ + qz− = 0

s = p + q

μB = μ◦_B + RT ln aB

μB = pμ+ + qμ−

a+ = γ+m+ and a− = γ−m−

mean ionic chemical potential μ±

μ± = μB = pμ+ + qμ−

mean ionic molality m±

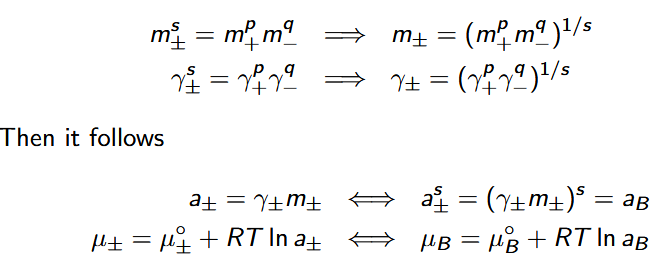
Debye-Hückel limiting law

og γ± = −|z+z−|AI ^½

where A = 0.5092 at T = 25◦C and I is the ionic strength of the

solution defined by

I = ½ ∑_i z^2_i m_i

In this expression zi is the charge of an ion i and mi is its molality

molality and molarity

in case of very dilute aqueous solutions, a volume of 1 L has a mass of 1 kg, so ___ have nearly the same values

electrochemical cell

consists of two electrodes (metallic conductors), in contact with electrolyte (an ionic conductor); they form two half-cells (compartments); difference in the electrical potential (voltage) between the electrode and the solution in each of the two half-cells; 

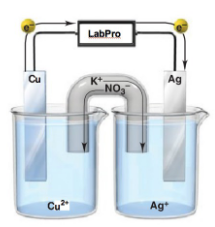
salt bridge

when electrolytes different, the two compartments are joined to complete the electrical circuit and enable the cells to function

galvanic (Daniell) cell

type of electrochemical cell that produces electricity as a result of the spontaneous chemical reaction occurring inside it

reaction quotient Q

Q = activities of products

activities of reactants = ∏_j a_j^ν_j

extent of reaction ξ

dimension of amount of substance and is reported in moles

Gibbs Free Energy given change in extent of reaction

∆G = = ∆G ◦ + RT ln Q

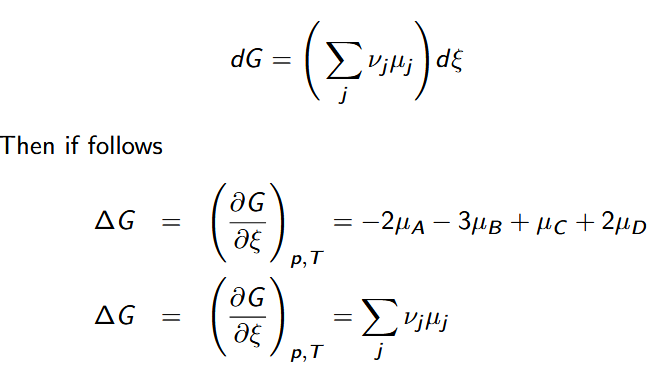
Nernst equation

∆G = −νFE_cell

E_cell = E^◦_cell − (RT/νF) ln Q

use a to account for non-ideality

Faraday’s constant

the charge per mole of electrons = −eN_A = 9.6485×10⁴ C/mol

redox reactions

type of chemical reaction in which the oxidation states of the reactants change; one loses electrons (oxidation), one gains electrons (reduction)

Universal Electrode Vessel

our version of the electrochemical cell

Cu electrode

CuSO4(aq)

Ag electrode

Salt bridge - KNO3(aq) + agar gel

Fritted glass or small hole

Magnetic stirring bar

Thermometer

Stirring plate

Reaction mixture start

1.00 x 10^-4 M AgNO₃(aq)

1.00 x 10^-3 M NH₄NO₃(aq)

work-horse equation

1) Obtain the apparent value of the “const.” from an initial measurement of Ecell with a solution of known mAg+ ≈ [Ag+]. (calibration step)

2) Then use “const.” and Ecell to deduce mAg+ ≈ [Ag+] when other equilibria are taking place (i.e. when you add other reagents)

3) Follow the lab write-up for calculations.

precipitate forms

Since the initial values of silver and chloride concentration were equal before precipitation (equal number of moles were added), after the precipitate forms the concentrations remaining in solution will also be equal

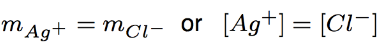
ion product

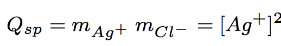
solubility product