Capacitance

Capacitance

The charge stored per unit pd in a capacitor

Capacitor

An electrical component that stores charge made of two parallel conducting plates with an insulator between them (dielectric)

Dielectric

An insulating material placed between the two plates of a capacitor in order to increase the amount of charge it can store

Permittivity of free space ε₀

A measure of the ability of a vacuum to allow an electric field to pass through it

Relative Permittivity/dielectric constant

The ratio of a charge stored in a capacitor with the dielectric to charge stored without the dielectric

Permittivity ε

A measure of the ability to store an electric field in the material

Polar molecules

Molecules with a positive and negative end (therefore has their own electric field)

If no electric field: arranged in random direction

If electric field: move and align themselves within the field (follow field lines)

What does the strength of a polar molecule’s electric field depend on

The strength of the dielectric’s permittivity, which opposes the capacitor’s field thus reducing the capacitor’s field strength.

Therefore potential difference required to charge capacitor decreases

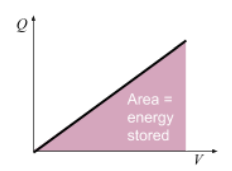
Area under charge against potential difference graph

Energy stored by a capacitor

Grad 1/C so C constant

E = ½QV

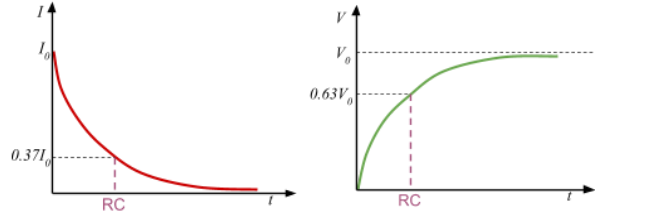
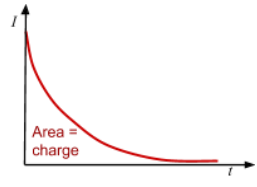
Shape of current against time for charging a capacitor

Area = Charge

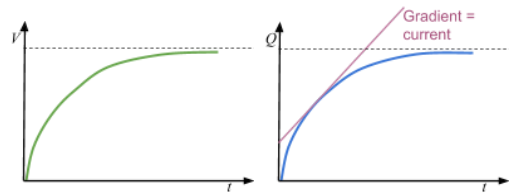
Shape of p.d/charge against time for charging a capacitor

Gradient of Q against t = current

Explain why the charging graphs have their shape

Once the capacitor is connected to a power supply, current starts to flow and negative charge builds up on the plate connected to the negative terminal

On the opposite plate, electrons are repelled by the negative charge building up on the initial plate, therefore these electrons move to the positive terminal and an equal but opposite charge is formed on each plate, creating a potential difference

As the charge across the plates increases, the potential difference
increases but the electron flow decreases due to the force of electrostatic repulsion also increasing, therefore current decreases and eventually reaches zero

Shape of current/p.d/charge against time for discharging a capacitor

I against t: Area = charge

Q against t: Gradient = current

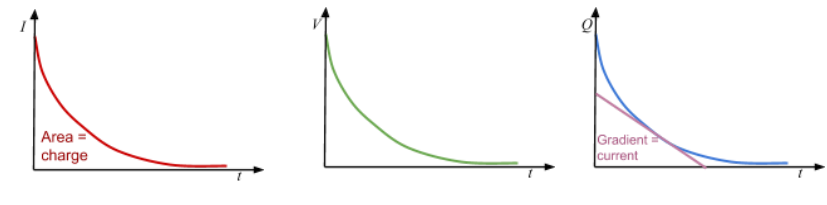
Explain why the discharging graphs have their shape

When the capacitor is discharging the current flows in the opposite direction, and the current, charge and potential difference across the capacitor will all fall exponentially, meaning it will take the same amount of time for the values to halve

Charging and discharging equations

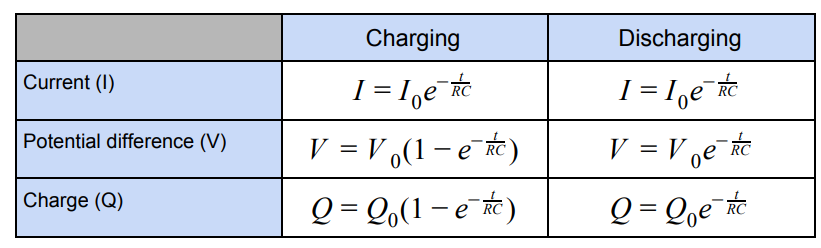
Time constant

t = RC

Value of time taken to:

Discharge a capacitor to 1/e ≈ 37% initial value (of Q,I or V)

Charge a capacitor to (1-1/e) ≈ 63% of its initial value (of Q or V)

How to find time constant from a graph of Q/I/V against time

Find the time where the values are either 0.37 of the initial value if discharging or 0.63 of the maximum value if charging