Sorting algs

Sorting algs for DS use https://visualgo.net/en/sorting

In-Place sorting

The algorithm only uses O(1) extra memory beyond the input array

Stable

Equal keys maintain their original order.

Adaptive Sorting

A sorting algorithm is adaptive if it runs faster on nearly sorted input.

Meaning:
It detects order and reduces work.

Bubble Sort Idea:

Repeatedly swap adjacent out-of-order elements until array is sorted.

How it works:

• Compare arr[i] and arr[i+1]

• If out of order → swap

• One full pass “bubbles” the largest element to the end

• Repeat until no swaps

Time Complexity:

• Worst: O(n²)

• Average: O(n²)

• Best: O(n) (if the array is already sorted — because we detect no swaps)

Space: O(1) Stable: ✔ Yes In-place: ✔ Yes Adaptive: ✔ Yes (stops early if sorted)

Bubble Sort RT

Best: O(N) - sorted array

Avg: O(N²)

Worst: O(N²)

2⃣ Selection Sort

Idea:

Repeatedly find min element and place it at the front.

How it works:

• Find smallest element in the unsorted part

• Swap it into the first unsorted position

• Move boundary forward

• Doesn’t matter if array is partially sorted — still scans entire unsorted part

Time Complexity:

• Worst / Avg / Best: O(n²)
  (because it always scans remaining elements)

Space: O(1) Stable: ❌ No (because selecting + swapping breaks order) In-place: ✔ Yes Adaptive: ❌ No

Selection Sort RT

O(N²) for all

3⃣ Insertion Sort

Idea:

Build the sorted array one element at a time by "inserting" each element into the correct spot.

How it works:

• Take element arr[i]

• Shift elements right until you find where it belongs

• Insert it there

Time Complexity:

• Worst: O(n²)

• Avg: O(n²)

• Best: O(n) when already sorted

Space: O(1) Stable: ✔ Yes In-place: ✔ Yes Adaptive: ✔ Yes

(very fast on nearly-sorted data)

Insertion Sort RT

Same as bubble sort

Best: O(N) - sorted array

Avg: O(N²)

Worst: O(N²) - Reverse sorted array

4⃣ Shell Sort

Idea:

Generalized insertion sort using gaps > 1 so elements move long distances efficiently.

How it works:

• Pick a gap sequence (e.g., n/2, n/4, … 1)

• Perform “gapped insertion sort”

• Reduce gap until gap = 1

• Final pass is a standard insertion sort on a mostly-sorted array → fast

Time Complexity:

Depends on gap sequence:

• Worst: ~O(n²)

• Good sequences: O(n^(3/2)), O(n^(4/3)), or even O(n log² n)

Space: O(1) Stable: ❌ No (because of gaps) In-place: ✔ Yes Adaptive: ❌ Not necessarily, depends on sequence

Shell sort RT

Best: O(N^(3/2)) - sorted array

Avg: O(N²)

Worst: O(N²)

5⃣ Quick Sort

Idea:

Divide-and-conquer: choose a pivot, partition into < pivot and > pivot, recurse.

How it works:

1. Pick a pivot

2. Partition array into:

   • left: elements < pivot

   • right: elements > pivot

3. Recursively sort left and right

Pivot choices:

• First element

• Last element

• Random

• Median-of-three

Time Complexity:

• Worst: O(n²) (e.g., sorted input with bad pivot)

• Average: O(n log n)

• Best: O(n log n)

Space: O(log n) for recursion Stable: ❌ No In-place: ✔ Yes Adaptive: ❌ No Notes:

Most efficient average-case sort in practice

Quick Sort RT

Best: O(nlogn )

Avg: O(nlogn)

Worst: O(N²) - sorted array with a bad pivot

6⃣ Merge Sort

Idea:

Divide-and-conquer: split array in half, sort each half, merge sorted halves.

How it works:

1. Divide array in the middle

2. Recursively sort left & right

3. Merge the two sorted halves using a temp array

Time Complexity:

• Best / Avg / Worst: O(n log n)

Space: O(n) (requires temp array) Stable: ✔ Yes In-place: ❌ No Adaptive: ❌ No Notes: Best guaranteed worst-case behavior.

Merge sort RT

O(nlogn) for everything

7⃣ Radix Sort

Idea:

Sort by digits (least significant first) using buckets or stable counting sort.

How it works:

For base-10 numbers:

• Sort by 1s digit

• Sort by 10s digit

• Sort by 100s digit

• …

Must use a stable sub-sort.

Time Complexity:

If numbers have k digits:

• O(k·n)

If k = constant → linear time O(n)

Space: O(n + k) Stable: ✔ Yes In-place: ❌ No (needs buckets) Adaptive: ❌ No Notes: Good when keys are numeric and digits small.

Radix RT

O(N) for everything

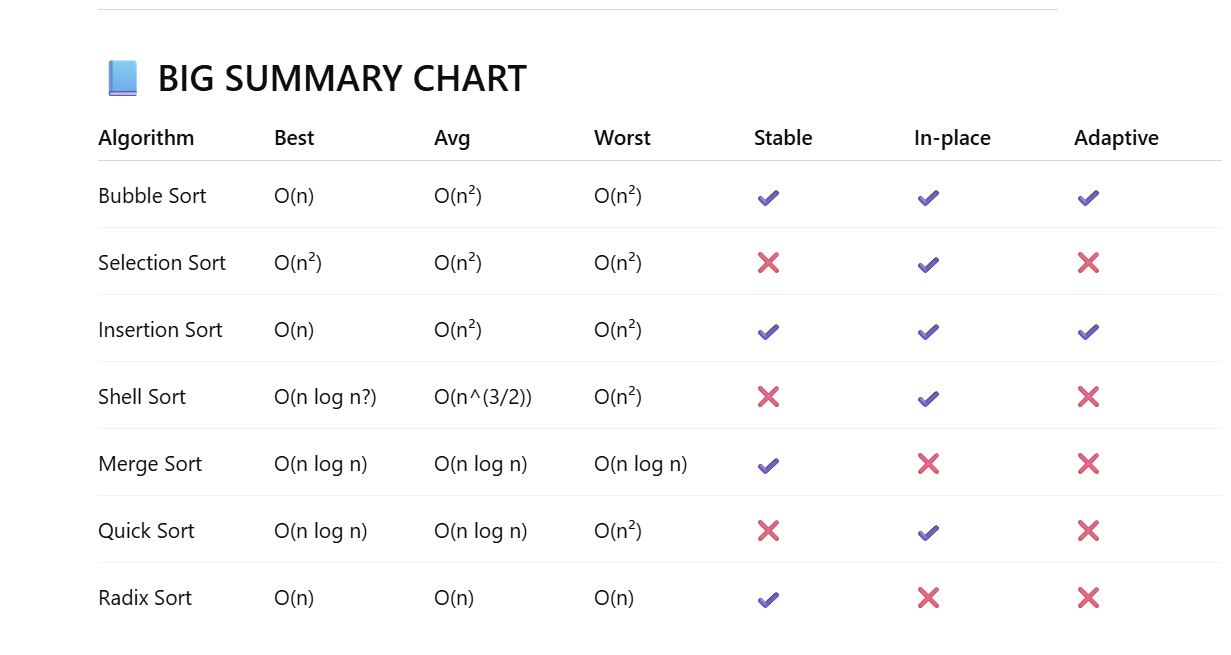
Which two have the same for every case

Merge and selection

Merge - O(nlogn)

Selection - O(n²)

Induction

Prove that if T = n something for 1 step, it’ll equal the same thing for T= n+1

State base case and verify numerically

State hypothesis- Assume true for n = k

Algebra - start from n = k+1 (or n=2k for recurrences on powers of two) and substitute hypothesis where needed

Conclude true for all n

Insertion and bubble sort have the same runtimes and properties

True

Stable

Bubble insertion merge radix