Further Maths Discrete / Statistics: Graphs and networks Section 1: Definitions

Mr Qureshi Statistics Further Maths

Loop

an edge with the same vertex at both ends.

Edges / Arcs

Set of lines connecting edges

Vertices / Nodes

Edges on a graph

Degree / Order (of a vertex)

the number of edges incident on it

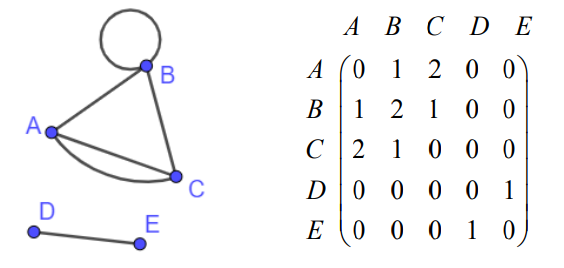
Adjacency Matrix

A way of representing a graph
shows the number of edges that connect each vertex directly with another vertex.

Trail

a sequence of edges in which the end of one edge (except the last) is the beginning of the next, and no edge is repeated

Cycle

a closed trail in which no vertex is repeated

Closed Cycle

the final vertex is the same as the start vertex

Hamiltonian cycle

a cycle which visits every vertex. Since a cycle is defined as a trail in which no vertex is repeated, a Hamiltonian cycle visits each vertex exactly once.

Connected Graph

one in which every vertex is joined, directly or indirectly, to each of the other vertices.

Simple Graph

a graph with no loops and no multiple edges

Simple-connected Graph

a graph that is both simple and connected.

A complete graph with n vertices is denoted by K_n and has

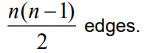
Tree

a simple-connected graph with no cycles.
A tree with n vertices has n −1 edges.

Bipartite Graph

a graph whose vertices are divided into two distinct sets. All edges go from a vertex in one set to a vertex in the other set.

Digraph

one or more edges that are directed: these edges have an arrow to indicate that you can only go in one direction.a graph whose vertices and edges form subsets of the vertices and edges of a given graph.

Subgraph

a graph whose vertices and edges form subsets of the vertices and edges of a given graph.